一个含指数项的新自治混沌系统的动力学分析

高智中

（安徽科技学院 理学院，安徽 凤阳 233100）

1963年Lorenz发现了第一个混沌系统［1］，此后混沌在非线性科学领域备受关注，混沌的发展经历了从认识了解、深化研究到工程应用等多个不同阶段.1999年，香港城市大学陈关荣教授等提出了Chen系统［2］.在Lorenz系统和Chen系统基础上，吕金虎和陈关荣又进一步提出了Lü系统［3］.这三个系统在结构上类似，但拓扑不等价.2002年，陈关荣和吕金虎还通过引入一个可变参数，提出了一个统一的混沌系统即Lorenz系统族［4］.此后，国内外不少学者提出了以Lorenz系统为基础的若干变形的新混沌系统［5－8］.新混沌系统的不断提出，进一步促进了人们对混沌现象更深入的认识和研究，丰富和完善了混沌学的研究内容，从而也提高了混沌理论在保密通信、图像加密、故障诊断和信号检测等方面的工程应用能力.但目前含指数项的混沌系统的研究甚少.

本文构造了一个含指数项的新三维连续自治混沌系统，其方程结构特别简单，含有两个参数和两个非线性项.利用相图、时间响应、功率谱、Poincaré映射、Lyapunov指数谱和分岔图等数值方法，验证了该系统在较宽的参数区间内能产生混沌信号，具有丰富的动力学特性.

1 新混沌系统数学模型

本文构造的新混沌系统的动力学方程为

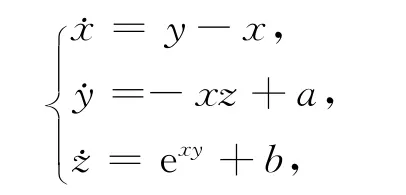
图1 系统的混沌吸引子Fig.1 Chaotic attractors of system

2 系统处于混沌时的时间历程、功率谱和Poincaré映射

系统混沌运动的时间历程具有非周期性，解的流对初值极为敏感，其时间历程图如图2（a）.混沌吸引子的非周期性也可以通过系统的连续功率谱表现出来，这里采用快速傅里叶变换法，对系统状态变量x的时间历程做功率谱分析得功率谱图如图2（b），由于混沌是非周期的，所以它的功率谱是连续的.混沌系统的Poincaré截面上是沿一条直线段或一条曲线弧分布着一些具有分形结构的密集点，图2（c）给出了系统在x＝0 平面上的Poincaré映射.由这些图都可以说明该新系统的确是一个混沌系统.

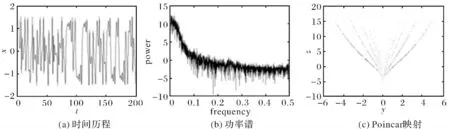
图2 混沌特性图Fig.2 Chaotic characteristics diagram

3 系统的Lyapunov指数和分形维数

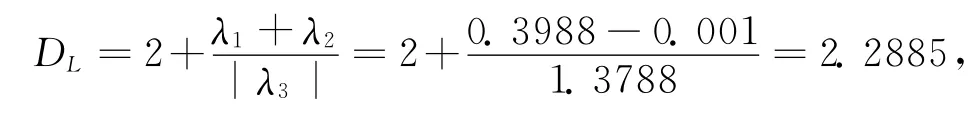
4 平衡点分析

为了求出系统的平衡点，当参数a＝0，b＝－4时，令˙x＝˙y＝˙z＝0，可求得系统的2个平衡点O（1.1774，1.1774，0）和P（－1.1774，－1.1774，0）.对系统进行线性化，得其雅可比矩阵为

将平衡点O和P分别代入雅可比矩阵，用Matlab计算特征值都为0.3332±2.5582i，－1.6663，可见这两个平衡点均为三维空间中的不稳定的鞍焦点.因此选取参数a＝0，b＝－4，系统可产生混沌现象.

5 系统参数的影响

非线性动力系统的状态主要是由系统参数决定，当参数取a＝0，b＝－4时，系统处于混沌状态.首先固定b＝－4，改变参数a，a∈［－3，3］，系统关于x的分岔图以及所对应的Lyapunov指数谱如图3所示.由图3可见系统由倍周期分岔进入混沌状态，然后由倒倍周期分岔进入稳定的周期一轨道，系统在参数a的正负区间的动力学行为具有对称性，并且通过数值仿真发现，随参数a的绝对值从0增加到1.6时两翼对称且均匀的吸引子逐渐演化为一翼吸引子.图4给出了系统在对称区间的典型参数下的吸引子.然后固定a＝0，改变参数b，b∈［－4，0］，系统关于x的分岔图以及所对应的Lyapunov指数谱如图5所示.由图5可见系统经历较宽参数范围的混沌状态最后趋于一个有界点，并且在混沌区域有两处周期窗口.图6 给出了系统的典型参数下的吸引子.

图3 系统随a变化时的分岔图与对应的Lyapunov指数谱Fig.3 Bifurcation diagram and Lyapunov exponents spectrum of the system when avaries

图4 系统随a变化时的相图Fig.4 Attractors of system when avaries

图5 系统随b变化时的分岔图与对应的Lyapunov指数谱Fig.5 Bifurcation diagram and Lyapunov exponents spectrum of the system when b varies

图6 系统随b变化时的相图Fig.6 Attractors of system when b varies

6 结论

本文构造并分析了一个含指数项的新三维连续自治混沌系统，其方程结构特别简单，系统仅具有两个平衡点，利用数值方法验证了该系统是一个新的混沌系统，并分析了系统当参数变化时动力学行为的演化过程.所得结果为系统的电路设计和通信方案设计等提供了理论依据.

［1］Lorenz E N.Deterministic nonpefiodic flow［J］.Atmos Sci，1963，20（2）：130－141.

［2］Chen G，Ueta T.Yet another chaotic attractor［J］.International Journal of Bifurcation and Chaos，1999，9（7）：1465－1466.

［3］LüJ H，Chen G R.A new chaotic attractor cioned［J］.International Journal of Bifurcation and Chaos，2002，12（3）：659－661.

［4］LüJ，Chen G，Cheng D S，et al.Bridge the gap between the Lorenz system and the Chen system［J］.International Journal of Bifurcation and Chaos，2002，12（12）：2917－2926.

［5］Liu C X，Liu T，Liu L，et al.A new chaotic attractor［J］.Chaos Solitons and Fractals，2004，22（5）：1031－1038.

［6］Qi G Y，Chen G R，Du S Z，et al.Analysis of a new chaotic system［J］.Physics A，2005，352：295－308.

［7］王杰智，陈增强，袁著祉.一个新的混沌系统及其性质研究［J］.物理学报，2006，55（8）：3956－3963.

［8］刘扬正，林长圣，李心朝.新的具有光滑二次函数混沌系统的构建与实现［J］.物理学报，2011，60（6）：1－5.

［9］张晓丹，李志萍，张丽丽.一类基于奇异值分解的Lyapunov指数 计 算 方 法［J］.北 京 科 技 大 学 学 报，2005，27（3）：371－374.