临界线上的RIEMANN-ZETA函数的定量估计
范云艳
(华北水利水电学院,河南郑州450045)
RIEMANN-ZETA函数是数学核心问题之一,也是数论的一个重要研究内容,对其临界值的估计曾吸引了国内外众多知名数学家的兴趣.
1 研究背景

当Res=σ>1时,函数定义为ζ(s)在除了s=1这个一阶简单极点外都是解析的,通过解析延拓可将式(1)推广至整个复平面s∈C.
RIEMANN-ZETA函数在整个分析学科乃至整个数学中扮演着重要的角色.最典型的例子就是关于整数中素数的分布情况及Zeta函数ζ(s)在0≤Res≤1区域中非平凡零点的分布情况.



对所有的t≠0均成立,这里Ο(·)是绝对常量.Littlewood在广义黎曼猜想下证明了Lindel9f猜想[4].
文中主要讨论临界线Res=σ=1/2上ZETA函数ζ(s)的定量估计.当Res=σ >0,N≥1时,RIEMANN-ZETA函数ζ(s)可表述为

为了得到ζ(1/2+it)的上界估计,数学家们付出了大量的努力.Littlewood[5]是第一个给出这个估计非平凡上界的人,他证明了:对于t≥e,有

Van der Corput[6]给出了

Huxley[7]证明了

截止目前,最好的估计结果是Lindel9f猜想

在广义黎曼猜想下Littlewood给出了Lindel9f猜想的证明.
通过运用Euler-Maclaurin求和公式的简单形式 YuanyouF Cheng 和 Sindey W Graham[8]给出了下面的估计结果.
如果t≥0,有

如果t≥2,有

如果t≥2,N为正整数,有

由此,笔者通过应用Euler-Maclaurin求和公式,讨论函数的单调性及函数极值,得到了关于RIEMANN-ZETA函数在临界线Res=σ=1/2上ζ(1/2+it)的更好的上界估计结果.
2 主要结论
引理1 根据文献[1],有 Euler-Maclaurin summation formula如下:
令函数f(x)在区间(a,b]上二阶连续可微.定义函数
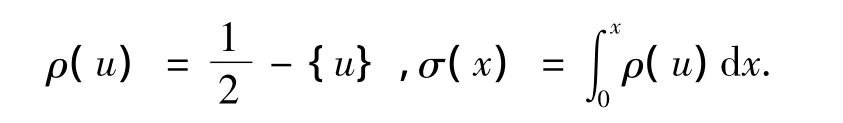
有

定理1 如果t≥0,有

推论1 如果0≤t≤e,有

3 定理证明
3.1 定理1证明
证明:对于Res=σ >1,任意的0<x<1,X充分大,由引理1,得

令X→∞,有

当σ >1,s≠1时,上式可作为ζ(s)的一个定义.
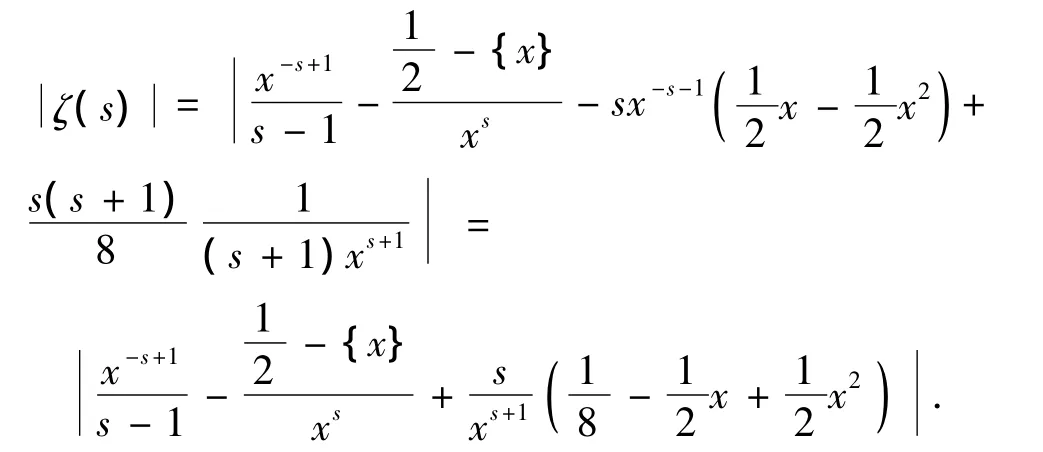

定理1证毕.
3.2 推论1证明
证明:对于0≤t≤e,由定理1,知

两边对f(t)求导,令f'(t)=0,可以得到f(t)的极点为t≈1.323 和t=0,且在(0,1.323)区间为减函数,在(1.323,e)区间为增函数.所以 f(t)在t=0取得最大值,得到

推论1证毕.
4 结 语

[1]张顺燕,张南岳.Riemann的Zeta函数简介[J].数学研究与评论,1984,4(3),134 -136.
[2] Lehmer D H.Extended computation of the Riemann zetafunction[J].Mathematika,1956,3(2):102 -108.
[3] Rosser J Barkley,Yohe J M,Schoenfeld Lowell.Rigorous computation and the zeros of the Riemann zeta-function(with discussion)[J].Information Processing,1969,68(1):70 -76.
[4] Anatolij A,Karatsuba.Basic analytic number theory[M].New York:Springer-Verlag,1993.
[5] Littlewood J E.Researches in the theory of the Riemann zeta function[J].Proc London Math Soc,1992,20(3):22-28.
[6] Graham S W,Kolesnik G.Van der Corput's method of exponentialsums[M].Cambridge:Cambridge University Press,1991.
[7] Huxley M N.Exponential sums and the Riemann zeta function[J].Proc.London Math Soc,1993,66(1):1 -40.
[8] YuanyouF Cheng,Sidney W Graham.Explicit estimates for the Riemann zeta-function[J].Rocky Mountain J Math 2004,34(4):1261 -1280.

