一种求取PV曲线的快速分解潮流法的改进

许 强，李 鹏

(华北水利水电学院，河南郑州450045)

在静态电压稳定性的研究中，PV曲线的求取具有重要意义.准确求取PV的曲线可以得到静态电压稳定的极限功率和电压临界值.我国电力系统已跨入超高压、远距离输电时代，快速准确地求取完整的PV曲线以获得电压稳定的极限功率和电压临界值具有重要意义［1］.常规潮流法的主要缺陷在于电压稳定极限附近雅可比矩阵奇异不收敛，而且这些算法一般针对每个节点单独进行考虑，可能扭曲系统的稳定状况［2］.因此必须谨慎地选择PV分析的节点，才能获得完整的系统信息.解决这一问题的核心就是改变雅可比矩阵元素，使雅可比矩阵在电压稳定极限处非奇异.有2种途径:一种是通过等效变换改变系统结构参数，如重负荷导纳法［3－4］;另一种是在常规潮流方程上增加参数方程［5－6］，如连续潮流法(Continuation Power Flow，CPF).

连续潮流法通过引入参数并采用预估－校正技术，求解增广潮流方程得到穿越雅可比矩阵奇异点的解曲线，是计算电压稳定极限的一种有效方法.目前制约CPF计算效率的瓶颈有两点:一是求解潮流方程时每次迭代都需要形成雅可比矩阵，在计算大系统时占用较多内存，计算量大，速度慢;二是步长控制困难，选取小的步长在CPF中是安全的，但导致计算效率低下，而不适当的大步长导致校正次数增多甚至不收敛.鉴于此，考虑在CPF的基础上结合快速解耦潮流法的特点，对连续潮流法进行改进，提出一种基于快速解耦法的局部参数化的连续潮流法，预测过程采用光滑插值技术，形成指定区间上的三次插值多项式与指定插值点的预测值，解决了计算量大和步长选择困难问题，能既快又准确地求取静态电压稳定极限.

1 连续潮流法原理

一般电力系统参数化后潮流方程为:f(x，λ)=0，式中:f∈Rn，x∈Rn，λ ∈ Rn，向量x包含系统中所有节点电压幅值和相角.潮流方程个数为n=2n1+n2，其中n1、n2分别为系统中的PQ和PV节点数.CPF的实现有4个步骤:参数化、预估、校正、步长控制［7］.采用常规潮流方程从初始值开始计算出基本潮流解(x(0)，λ(0))，目的是要得到在参数变化范围内的潮流解(x(i)，λ(i)).

2 快速解耦连续潮流法

2.1 基本算法

在电力系统潮流计算中，快速解耦法［8－9］(BX型)的修正方程式可以简化为

参数化后的潮流方程为

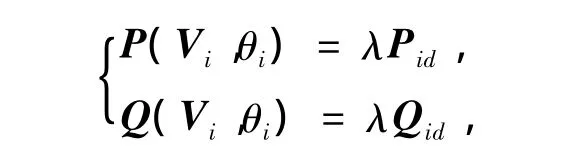
式中:Pid，Qid为节点负荷增长向量，V，θ为节点电压向量和相角，λ为负荷变化因子.假设系统有n个节点，其中第1至第m个节点为PQ节点，第n个节点为平衡节点，其余为PV节点.

当选取θk为参数时，修正方程为:

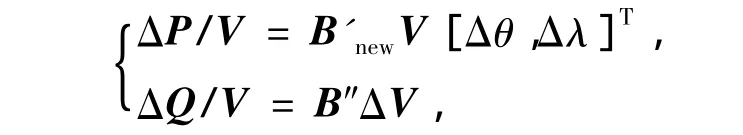
其中

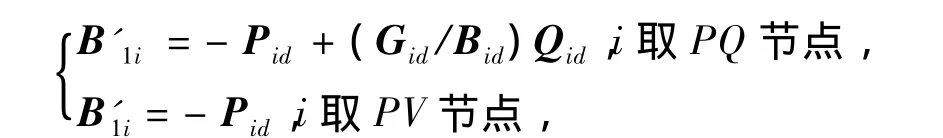
当选取Vk为参数时，修正方程为:

式中:ek表示与方程组维数相匹配的行相量，除第k个元素为1其余元素都为零，k为电压下降最快的节点.当潮流接近电压稳定极限时，弱节点负荷的电压(假定为Vk)变化最大，可选为参考变量.求解修正方程式是基于快速分解法的连续潮流法的关键，求解步骤可分为以下几步.

1)利用B'形成第一因子表，利用B″形成第二因子表，以后因子表不变.

2)给定各节点电压初始值，即PQ节点电压为1∠0°，PV 节点电压为 VSP∠0°.

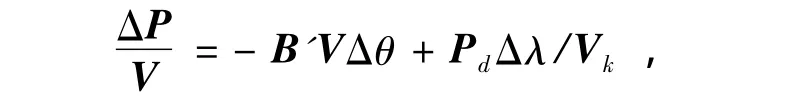
其中 Pd= ［P1d，…，P(n－1)d］T，求得 Δθ.

4)用 Δθ通过关系式 θ(k)= θ(k－1)+ Δθ(k－1)修正θ.

求得 ΔV1，…，ΔVk－1，Δλ/Vk，Vk+1，…，ΔVm，用 ΔV1，…，ΔVk－1，Δλ/Vk，ΔVk+1，…，ΔVm修正和 λ ，有关系式 V(k)=V(k－1)+ ΔV(k－1)，λ(k)= λ(k－1)+ Δλ(k－1)，k表示第k次迭代.

6)计算程序按1θ，1V方式进行迭代，也就是首先进行一次Pθ迭代，然后再进行一次θV迭代，之后再进行一次Pθ迭代，这样反复下去，直到各节点功率误差满足精度为止.

2.2 改进算法

影响连续潮流法计算效率的一个关键因素是步长的控制，若将步长选定很小，这样会导致计算效率低下，而选定不适当的大步长使预估值远离真实解，导致校正迭代次数增加甚至不收敛.理想的情况是，通过跟踪解曲线的形状来确定步长的大小，在求解曲线的平坦部分时采用较大步长，在求解曲线的非平坦部分时采用较小步长.但事实上是事先并不知道解曲线的形状，因此步长控制困难.

为解决步长控制困难问题，可以在预测和变步长时使用Akima方法的光滑插值技术来有效控制步长.在潮流初始状态(λ0=0)，用快速解耦法求得初始潮流解Vk0.给定系统负荷变化方式变量Yd以后，以λ为参数变量，采用改进参数的CPF潮流法求解系统潮流解 Vik，λi= λi－1+ Δλ(i=1，2，…).若节点k电压Vk降落最大，Vk表示节点k在不同运行方式下的电压向量.因此可以得到曲线上一离散点系列 (Vk0，λ0)，…，(Vki，λi)，根据 Akima 几何条件，取i=5较合适.插值方程表示如下:

根据Akima几何条件(取gt为中间值)可得:

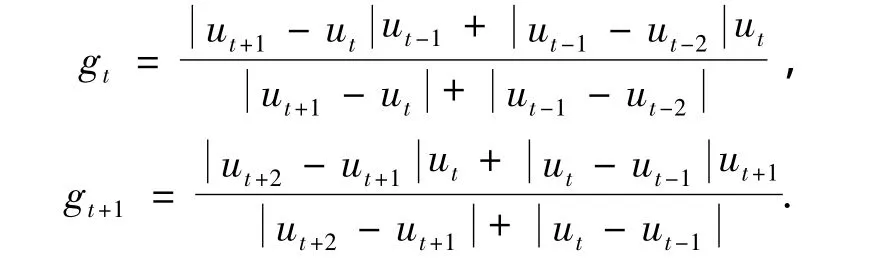
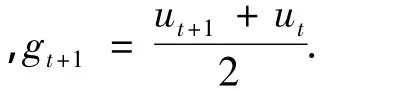
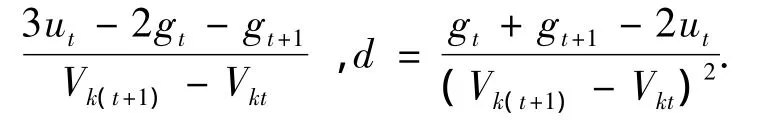
由插值方程求得λ(k).以Vk作为局部参数，用局部参数CPF修正潮流得到潮流解，最后用最新得到的离散点反复进行光滑插值，可迅速求取静态稳定极限.

2.3 算例分析

以IEEE39节点系统为例，编制相应的标准程序计算并作对比.分析过程中选取所有节点按原功率比例及等功率因数方式增加负荷.图1为IEEE39节点系统节点3，节点8，节点12的PV曲线.

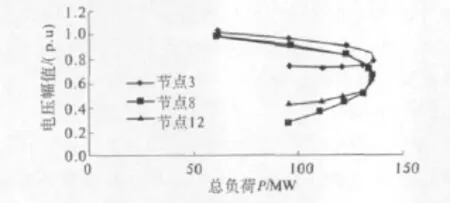
图1 IEEE39节点系统PV曲线

由图1可知，采用改进的方法可绘出完整的PV曲线，并且在功率极限点未遇到不收敛问题.图2为采用文献［5］算法和改进算法求取IEEE39节点系统节点5的PV曲线.

图2 IEEE39节点系统对比PV曲线

由图2可知改进算法与文献［5］算法绘制的PV曲线吻合，验证了算法的正确性.

3 结语

连续潮流分析方法是解决潮流问题收敛困难的理想方法，然而他需要对多个工作节点进行潮流计算，计算量较大，非常耗时.因而提高潮流的计算速度非常必要，笔者提出一种基于快速解耦法的改进连续潮流算法.由于采用BX型快速分解方法，在每次求解修正方程时不需要重新形成雅可比矩阵，因而计算量小，占用内存较少，速度快.

在预测和变步长时采用Akima方法的光滑插值技术的同时，校正过程仍然采用局部参数化.这种变步长的方法有效解决了步长难于控制的问题，能准确地求取各节点完整的PV曲线.

［1］ 王锡凡.现代电力系统分析［M］.北京:科学出版社，2003.

［2］程浩忠，吴昊.电力系统无功与电压稳定性［M］.北京:中国电力出版社，2004.

［3］张尧，宋文楠，苏碧萍.无功补偿对静态稳定的影响［J］.电力系统及其自动化学报，1994，6(2):16 －21.

［4］张尧，曾绍标，王琴，等.节点PV曲线的快速求解方法［J］.电力系统自动化，1999，23(9):19 －21.

［5］李新星，韩富春，李少华，等.一种求取PV曲线的改进连续潮流算法研究［J］.水电能源科学，2010，28(4):142－144.

［6］张尧，张建设，袁世强.求取静态电压稳定极限的改进连续潮流法［J］.电力系统及其自动化学报，2005，17(2):21－25.

［7］姚玉斌，刘莉，陈学允.基于快速分解法的连续潮流法［J］.哈尔滨工业大学学报，2000，32(2):128 －131.

［8］ Kundur P.Power System Stability and Control［M］.New York:McGraw-Hill Inc.，1994.

［9］ Semlyen A，de Leon F.Quasi-newton power flow using partral acohian updates［J］.IEEE Trans.Power Systems，2001，16:332－339.