IGBT数值模型及其损耗规律研究
衣 鹏,王心坚,孙泽昌
(同济大学汽车学院新能源汽车工程中心,上海 201804)
0 引言
Baliga于1983年提出了IGBT的关断暂态模型,并验证了IGBT的PNP-MOSFET结构,但是由于存在一定的局限性,并未应用于电子仿真软件中[1]。Hefner于1988年提出了非准静态近似原理,并建立了Hefner模型[2],此模型被大量应用到各商业软件中,模型较为全面而且结果精确,但模型较为复杂,收敛性也不是很好。半数值模型是利用现有软件中的MOSFET模型和PNP模型组合而成的,虽然模型较为简单,但是由于IGBT内的BJT与传统BJT不太相同,所以准确度相对不如数值模型[3]。行为模型则是将IGBT视为一个黑箱,通过输出特性来描述IGBT。Monti运用模糊逻辑建立了IGBT模型,但是结果的精确度不足[4]。
为了准确分析损耗,采用的是数值模型,针对Hefner模型进行了相应的简化,得到了一个更为简单的简化模型,方便了模型在Matlab软件中的植入,加快了运算速度。然后,将该模型应用于测试电路中进行验证。将模型结果与商用软件中的Hefner模型进行了对比,验证了准确性。并在改变负载大小的情况下研究IGBT的损耗规律,对损耗规律进行了定性分析。
1 IGBT模型建立
1.1 物理模型的导出
绝缘栅双极性晶体管(IGBT)具有击穿电压大,最大饱和电流大的特点,是一种大功率电力电子元器件。以N沟道非穿通型IGBT为例进行分析。图1a给出了该IGBT的物理结构,从结构可以看出,在发射极(E极)和集电极(C极)之间形成了一个PNP结构的BJT,而在栅极(G极)下方则构成了一个MOSFET结构的导电沟道,于是就得到了之前所提到的IGBT就是一个MOSFET-PNP结构,如图1b所示。然而由于在这个PNP结构中,与传统的PNP结构的BJT不同的是该PNP的基区相对较宽,并不能直接用传统的BJT结构进行代替,这就是为什么半数值模型不精确的原因。而且由于耗尽区和栅极氧化物的存在,使得各极之间存在节电容和寄生电容。在Hefner的模型中,将用一个可控电流源来代替图1b中的PNP结构[5]。图2a中给出了Hefner模型在植入电力电子仿真软件SABER时的等效电路图[5]。本文的模型是在该模型的基础上进行了简化,简化的原则如下:
a.忽略雪崩倍增电流Imult。
b.忽略位于集电极的导通调制电阻,因为该电阻对于IGBT的动态开关过程影响不大,对于损耗的影响也就很小。
c.忽略电流源In(W)上的电压Vbd,这一电压的存在同Rb一样对于损耗计算影响不大,但却会大大增加计算量。
图2b中的简化对于IGBT的动态和稳态效应影响不是很大。首先,雪崩效应只有在大电场的情况下才会产生大的雪崩电流,在IGBT正常工作情况下对于电流和电压的影响很小。其次,调制电阻Rb主要影响到导通电阻的大小而且相对于MOSFET造成的影响相对可以忽略,对于开关过程影响不是很显著。再者,从图1中可以看出,Vbd是耗尽区节电容上的电压值,其电压值对于系统影响微小。通过以上分析可以看出简化的可行性。

图1 IGBT结构

图2 等效电路
1.2 双极输运理论
半导体中载流子分为电子和空穴,而载流子的运动又分为漂移运动和扩散运动。影响漂移和扩散的因素包括双极迁移率和双极扩散系数[2]。根据双极输运原理,可以得到:

根据Hefner模型中推导[6],可以得到x=W 处的电子电流和空穴电流为:

Q为基区载流子电荷量;QB为基区本底载流子电荷量;NB为基区本地掺杂浓度;ni为本征载流子浓度;Isne为反向电子饱和电流。
根据图2所示电子电流In(W)由流过 MOSFET的电流Imos、以及流过电容的电流组成,公式如下所示:
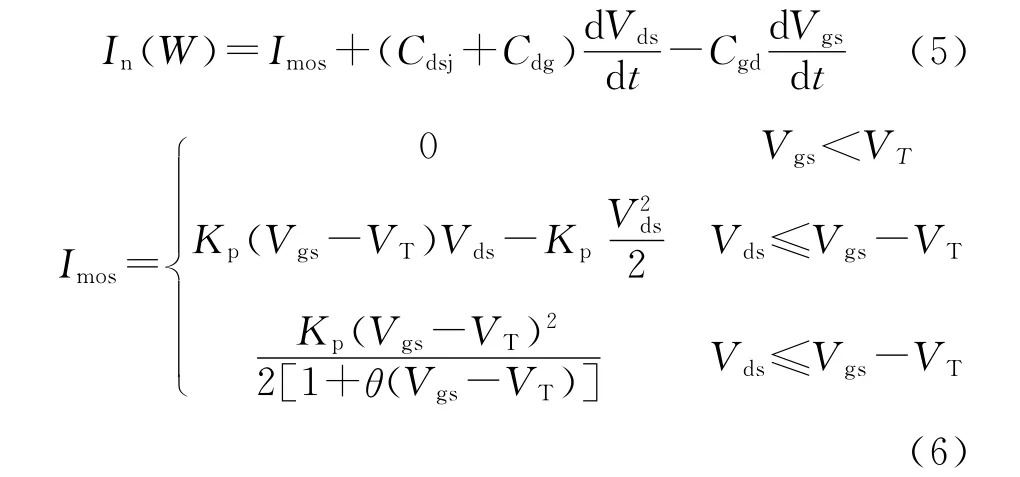
Kp为MOSFET跨导;θ为横向场跨导因数。
式(3)、式(4)和式(5)基本构成了模型。
1.3 模型的求解
模型求解的过程实际上是对式(3)、式(4)和式(5)的求解过程,可以看出,这是一个非线性微分方程组,求解很复杂。于是在此采用一阶前向差分代替微分,如式(7)所示。于是可以将该方程组变为非线性方程组。其中Vgs是已知量,且根据假设③可得Vds=Vcs=Vbe,于是求解的未知量就是In(W),Ip(W),Q,Vds。但是仅有3个方程,剩下的方程由KVL和KCL方程补足。非线性方程组的求解采用M语言编程实现。

2 IGBT模型的验证
建立好IGBT模型之后,将该模型应用于图3所示的电路之中,根据KVL定理可得到式(8)所示方程。于是经过计算可得图4所示的结果对比。其中,图4a给出了静态特性在不同Vgs情况下的ITVcs关系曲线,图4b、图4c将模型结果与Hefner模型结果进行了对比,分别给出了开启和关闭过程中电压暂态对比曲线和电流暂态对比曲线。
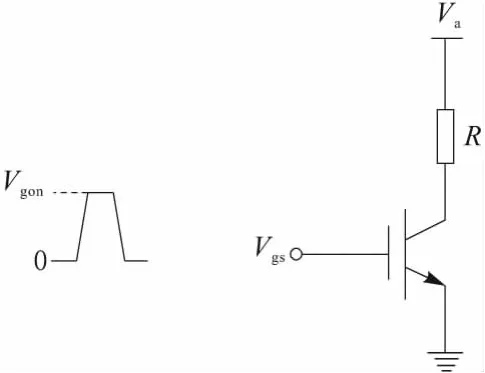
图3 测试电路

图4 IGBT模型

从图4中可以看出,该模型的仿真结果,关断暂态的电压电流波形与Hefner模型基本一致,这也变相证明了所作简化的可靠性,也同时证明了用该种模型来计算的损耗的可靠性。而在静态特性中可以看出存在一定差异,这是由于对于IGBT中的MOSFET电流有各种不同的公式造成,这也从侧面说明了开关过程中的损耗及拖尾电流的产生主要是由于基区的过剩电荷在MOSFET在关断之后慢慢放电产生的空穴电流Ip(W)。
3 不同负载下IGBT损耗规律
上面已经给出了IGBT的动态和稳态特性,正如之前提到,研究动态过程的重点在于计算IGBT的损耗,并研究IGBT的损耗随负载的变化规律,从而可以减小损耗。IGBT的损耗分为开关损耗和导通损耗,开关损耗又分为开启损耗和关断损耗。其中IGBT的开启和关断东芝公司给出了定义。开启时间指Vge从电压的10%开始到Vce电压下降到10%为止。关断时间指Vge从电压的90%开始到IT下降到10%为止。
根据上述定义,可以求出IGBT的各损耗结果,如表1所示。

表1 IGBT的各项损耗
影响IGBT损耗的原因很多,包括驱动电路的电压上升时间、负载电流、负载电压以及控制开关的频率等。而一般的逆变器中的IGBT一般工作在额定电压下,所以,主要研究了IGBT损耗随负载的变化关系。在图3给出的测试电路中,只要改变负载电阻R,就可以改变负载电流的大小。图5中给出了各损耗随负载电流的变化曲线。从图5中可以看出,IGBT的开启损耗的变化率随着电流的增加逐渐变大,而关断损耗变化逐渐趋于平缓。产生这种现象的原因尚未完全得知,但可以肯定与IGBT模型中的节电容有关,节电容对于IGBT损耗影响如图6所示。从图6可以看出,当电流方向如图所示的时刻,节电容必定会产生电流,这个电流有利于电压的增加,却会阻碍电压的减小,这样就会增加开启损耗,却会减小关断损耗。而且这种效应会随着电流的增加而增大。不同负载电流下IGBT电压的对比如图7所示。从图7中可以看出,大电流情况下,电压下降(开启)时的曲线明显平缓,而正向电压升高(关断)时,电压曲线相对陡峭。此现象的出现也从侧面证明了上述理论。至于确定的数值关系还需要进一步深入研究。
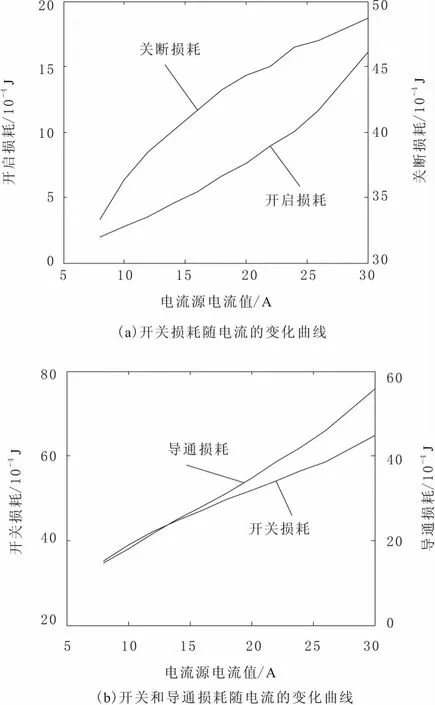
图5 IGBT损耗随负载电流的变化曲线

图6 节电容对于IGBT损耗影响
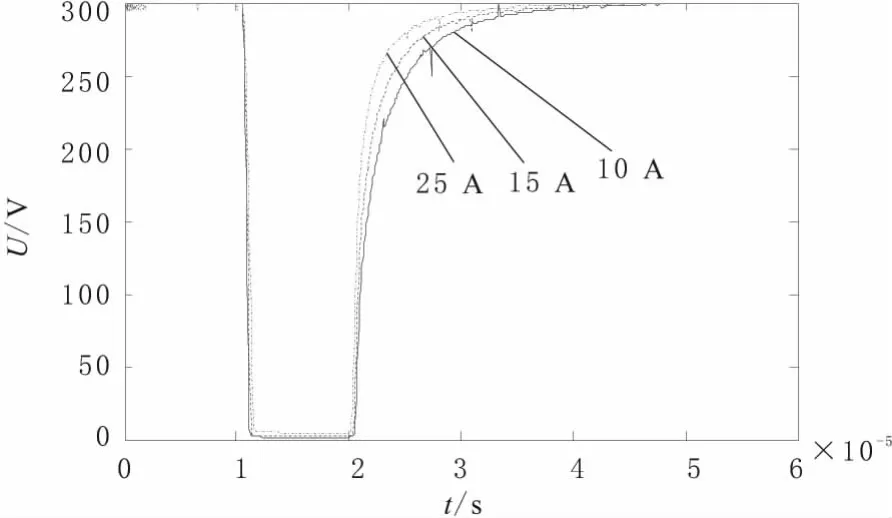
图7 模型不同负载电流下IGBT电压的对比
4 结束语
在Hefner模型的基础上,建立了简化的IGBT数值模型,通过仿真分析验证了这一模型的可靠性。在此模型的基础上,分析了IGBT的损耗与负载电流之间的关系,这也是分析电机控制器损耗的基础。然而,IGBT模型还存在一些不足,比如模型的稳定性和计算的快速性等,这也是需要进一步改善的。
[1]Baliga B J.Fast-switching insulated gate transistors[J].IEEE Electrons Device Letters,1983,4(12):452-454.
[2]Hefner A R,Blackburn D L.An analytical model for the steady-state and transient characteristics of the power insulated gate bipolar Transistor[J].Solid-state Electronics,1988,(31):1513-1532.
[3]李 平.NPT型IGBT电器模型及参数提取[D].杭州:浙江大学,2009.
[4]Monti A.Fuzzy-based black-box approach to IGBT modeling,in Proc[A].IEEE Int.Conf.Electron,Circuits,Syst[C].1996,(2):1147-1150.
[5]Hefner A R,Diebolt Jr D M.An experimentally verified IGBT model implemented in the saber circuit simulator[J].IEEE Trans.Power Elec.,1994,9(5):532-542.
[6]Chang Su Mitter,Allen R Hefner,Jr,Dan Y.Chen,Fred C.Lee,Insulated gate bipolar transistor(IGBT)modeling using IG-SPICE[A].IEEE Industry Applications Society Annual Meeting[C].1991,(2):1515-1521.

