电磁轨道炮的电路仿真建模

潘 娜，韩学军

(东北电力大学电气工程学院，吉林 吉林 132012)

0 引言

根据公开的试验现状，试验中电磁轨道炮的弹丸速度达7 Ma，射程可达370 km。我国电磁轨道炮研究有了较大发展，在实验技术与数值仿真方面均取得了一些研究成果［1－2］。电磁轨道炮的运行过程复杂，其中包括复杂的机械、电磁、热等物理过程，且相互耦合［3－4］。针对电磁轨道炮的研究内容很多，基于不同方向的研究与方法不同，其中包括电磁轨道炮发射、电磁轨道炮仿真建模、脉冲时序控制电源、电枢特性研究、动态负载特性研究、炮体结构设计与电感梯度研究等［5－13］。

研究建模随方法进行变化，采用Simulink软件进行仿真［6－10］，对电磁轨道炮采用简化建模，没有考虑导轨动态的电阻和电感，没有达到对电流和运动过程的同步求解;采用Ansys或Ansoft软件进行有限元数值方法分析轨道炮的电磁分布［11］，根据一些点的数据分布进行统计分析，使用解析解验证分析正确性。

本课题研究背景，即电磁轨道炮的电路方法仿真，使用Matlab程序计算电路层次的对电磁轨道炮建立的模型参数，其中轨道采用可变电阻和可变电感模型等效，形成以电容电压和电感电流为变量的状态方程组;采用差分法表示，形成迭代求解的过程;在对电容电压、电感电流波形进行迭代求解的同时，利用电枢受电磁力与电感梯度的关系求解电枢的运动过程，电枢运动又通过影响轨道电阻、电感参数来影响电容电压、电感电流的求解，从而使求解成为考虑电流、运动的同步求解，该模型的动态特性和实际过程一致。对比有实验数据的文献结果［14］，误差在允许范围内，仿真结果证明了该方法的正确性和有效性。

1 电磁轨道炮电路模型建立

电磁轨道炮的基本结构是由高功率脉冲电源、2根导电轨道、夹在2根轨道间可以滑动的电枢组成。工作原理是由高功率脉冲电源输出的电流经轨道流经电枢，电流回路产生的大磁场与电枢中的大电流相互作用，产生推动电枢前进的电磁力。

电磁轨道炮集中参数模型的等效电路图如图1所示。其中Ci为储能电容;Dj为晶闸管，控制Ci的放电时序;Rci为电容支路的等效电阻;Dk为续流二极管，在电容放完电时为电感放电提供续流回路;Rxi为续流回路的等效电阻;Lsi为调波电感;Rsi为调波电感的电阻;Rbi为由电容器连接到轨道电缆等效的电阻;Lbi为电缆等效的电感;Rx和Lx分别为轨道等效的随电枢运动而变化的电阻和电感;Ra为电枢的电阻;Rx=Rx0+R'x;Lx=Lx0+L'x;Rx0;Lx0分别为在电枢处于初始位置时轨道的等效电阻和电感;R'和 L'为轨道的电阻梯度和电感梯度;i=1，2，…，n;j=1，3，5，…，n;k=2，4，6，…，n。

图1 电磁轨道炮集中参数电路模型Fig.1 Electromagnetic railgun lumped parameter circuit model

等效电路中，对晶闸管和二极管采用简单的开关模型代替，即管上电压达到导通要求马上导通，当电流反向 (对晶闸管)或电压不够导通 (对二极管)时即立刻截止。在导通过程中，也考虑了管子的导通电压和导通电阻等参数。

电路中含有电容和电感，等效电路建立状态方程组，以储能电容Ci的电压uCi，以及调波电感Lsi的电流iLi为变量，可列状态方程组如下:

其中，i为轨道的电流。

在方程式中:

将式(3)代入式(1)中，可得到最终关于uCi和iLi的状态方程组。

式(1)是在电容器进行放电时的电路方程，当电容放电结束后，由调波电感通过续流回路进行放电时，状态方程组也相应发生改变。由于电容器通过晶闸管控制放电，故当电容器放电结束，续流回路工作后，电容器支路由于电流过小将自动断开，故在后面时间步的计算时就不再考虑电容器电压。

2 电路模型的迭代求解

对形成的状态方程组求解，需要采用数值离散方法，通过程序来求解。最简单有效的方法是差分法，用差分项代替方程组中的微分项，前项差分格式为

利用前项差分格式，可将上面的状态方程组(1)离散如下:

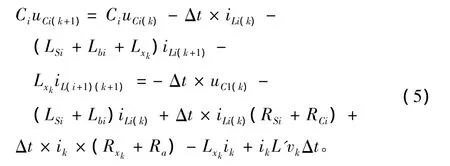
方程组中，下标k表示第k时刻即当前时刻的变量值，下标k+1表示第k+1时刻即下一时刻的变量值。由于电枢在运动，轨道的电阻Rx和电感Lx随其变化，且上面方程组含有的速度项也需要求得，故还需要有运动方程组。

把每个时间步电枢的运动近似看为匀加速直线运动，根据电枢受到的电磁力与轨道电感梯度的关系F=，可以求得当前时间步电枢的加速度ak，进而求解电枢下一时刻的速度vk和位移xk，并改变下一时刻的轨道电阻、电感及速度项，即不断更新上面的状态方程组，从而获得准确的电流波形和运动情况，离散的运动方程如下:

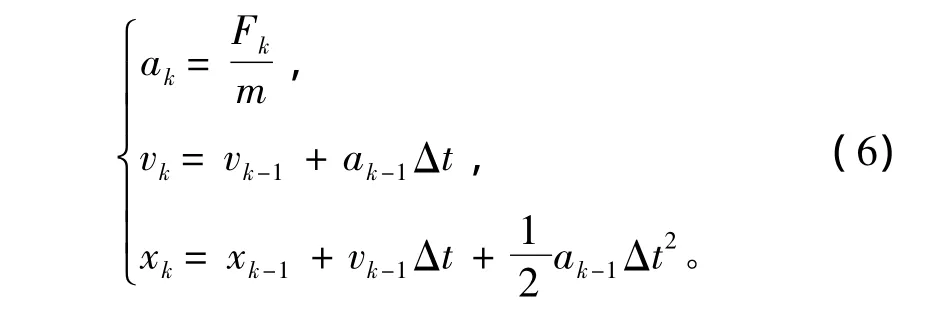
由以上离散后的电流状态方程组及运动方程，如果已知0时刻的uCi和iLi，以及电枢的初始速度v0和位置x0等，就可以一次迭代求解到以后各个时间步的 uCi，iLi和电枢速度 v、位置 x，获得最终的解答。

时间步长选取的依据是电流到达峰值时间的1%，一般到达峰值的时间为0.1 ms，即1 μs为一个时间步长进行迭代求解。

3 算法流程图

对电磁轨道炮电路建模求解的算法流程如图2所示。

流程图的各个步骤如下:

第一步:初始化，输入电路参数，初始条件。

第二步:判断电枢位移是否小于轨道长度。若小于，跳至下一步判断是否到达下一电容器投入时刻;若大于，进行最后一步后处理输出最后仿真结果。

第三步:判断是否到达下一电容器投入时刻。若达到，则改变电容器数目及相应变量、方程阶数;若没有达到，则判断各电容器是否放电完毕。

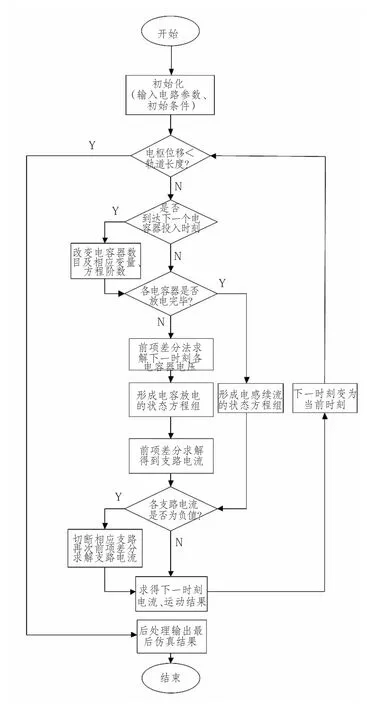
图2 算法流程图Fig.2 Algorithm flow chart

第四步:电容器组放电和其放电结束电感放电过程状态方程组是不同的，故需要在计算中加以判断。开始都是由各电容器组开始放电，首次计算某电容器放电时应以电容器放电的状态方程组进行计算，当计算到该电容器电压小于0即续流二极管导通时，续流支路开始工作，改变状态方程组到调波电感放电的状态。判断电容器支路断开条件为电容器电流反向。

若放电完毕，形成电感续流状态方程组;若没有完毕，则使用前项差分法求解下一时刻各电容器电压，形成电容放电的状态方程组，使用前项差分法求解支路电流。

第五步:判断各支路电流是否为负值，由于续流回路的二极管保证了每一支路电流不能为负值，因此当调波电感放电结束后，支路电流为负时，此支路电流计算错误，其他支路电流偏高;需要判断各支路调波电感是否放电结束，并且在某支路电流出现负值时将此支路人为切断而重新计算下一时刻的电流、运动结果，进而保证计算的准确性。

第六步:进行迭代计算，将下一时刻变为当前时刻，重复进行第二步到第五步。在第二步中，电枢位移大于轨道长度时，进入后处理输出仿真结果。

某支路调波电感已经放电结束，在随后的过程中由于其他支路的投入及电枢反电动势的变化造成此支路重新导通，需要每一时间步长会先尝试将所有支路都投入计算结果，进行电流值的判断。每一时间步长中计算2次电流，保证计算的可靠性和准确性。

第七步:结束计算。

4 模型仿真与验证

仿真实例采用文献 ［14］，该文献是Miguel Del Güercio在 U.S.ArmyResearch Laboratory 采 用PSPICE编写的轨道炮仿真程序结果与试验数据［9］。文献介绍了一整套轨道炮的实验装置，给出了比较详细的电容、电感、电缆参数，也给出了仿真时建立的电源模块模型，共18个电源模块同时或按时序放电触发，其仿真结果与实验结果比较吻合。

4.1 系统参数设置

试验电容储能总能量为4.5 MJ，采用18组单模块同时和时序放电。电枢质量为230 g，电容C为4.2422 mF，电容充电电压分别为5 kV和6.5 kV，电容串联电阻Rc为3.65 mΩ，续流二极管电阻Rx为6.65 mΩ，R'为0 μΩ/m，L'为0.46 μH/m，电枢质量为0.23 kg，初始位置x0为0 m，轨道长度l为3 m，电缆电阻Rb为9.18 mΩ，电缆电感Lb为3.22 μH。

同时触发中，前9个模块的调波电感Ls为60 μH，调波电感电阻Rs为2 mΩ，其他9个模块的Ls为24 μH，Rs为1 mΩ;时序触发的时间为前9个模块同时触发，剩余的9个模块按照依次延迟0.3 ms顺序触发。

4.2 仿真结果比较与分析

图3为基于本系统的仿真结果，电流的峰值分别为789.246 kA和661.949 kA，出口速度分别为867.391 m/s和955.055 m/s。文献中电流峰值分别为722.5 kA和481 kA，出口速度分别为880 m/s和1000 m/s。

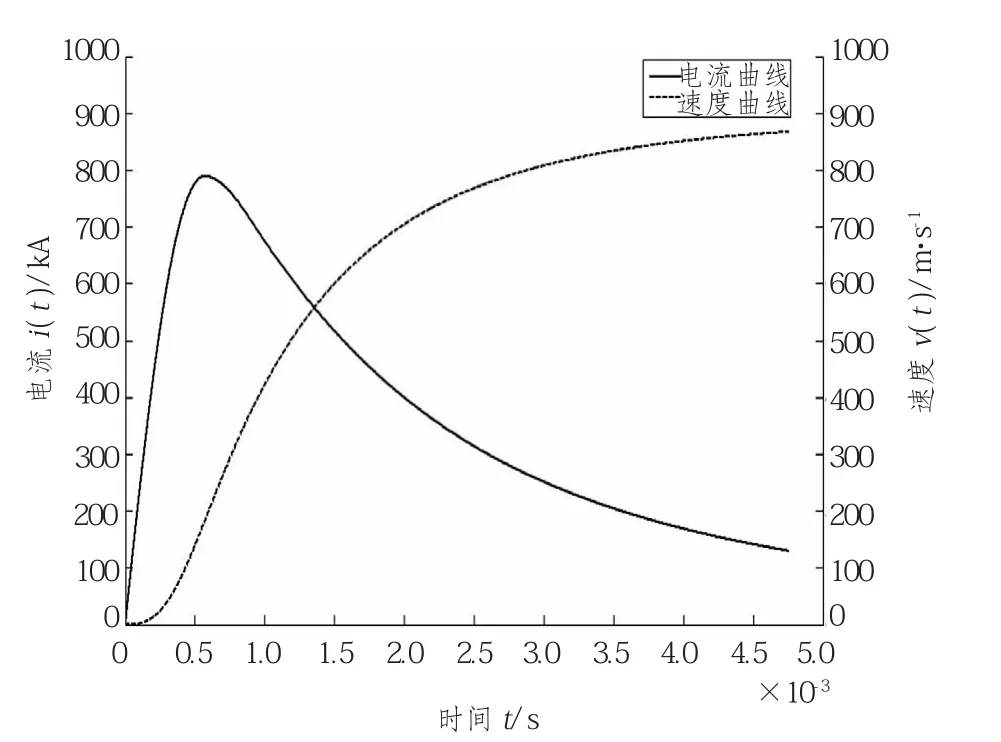
图3 5 kV的电流和速度曲线Fig.3 5 Kv current and speed curve

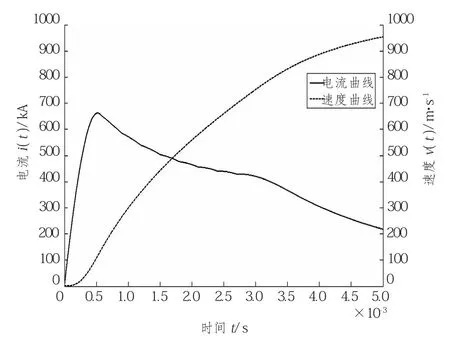
图4 6.5 kV的电流和速度曲线Fig.4 6.5 Kv current and speed curve

图5 文献中仿真与实测的电流曲线Fig.5 The literature simulation and measured current curve

图5为文献［14］中提供的仿真与试验电流曲线。由图可知，输入激励与输出电流获得好的一致性。在5 kV电压充电中，电流到达峰值时间和峰值与文献仿真和试验数据基本吻合，电枢出口速度误差率为1.4%;在6.5 kV电压充电中，电流到达峰值时间和峰值与文献有误差，波形保持在平顶波脉宽的时间基本一致，出口速度误差率为4.5%。比较文献仿真和试验数据与系统仿真结果可知，此算法建立的电磁轨道炮仿真模型可行。

5 结语

基于电磁轨道炮的基本结构和工作原理，利用电路方法仿真，使用Matlab程序计算电路层次的对电磁轨道炮建立的模型参数，轨道采用非固定值而为可变电阻和可变电感模型等效，采用差分法表示状态方程组，电磁力与电感梯度与轨道电阻、电感参数及电容电压、电感电流之间的相互影响，即迭代求解的同时成为考虑电流、运动的同步求解，算法的流程图给出所有的迭代运算过程，使得模型的动态特性和实际运动过程一致。对比有实验和仿真双重数据的文献结果，验证在误差允许范围5%内，系统结果证明了该运算方法的正确性和有效性。

［1］WANG Y，CHENG S K，ZHENG P.Widely developing electric launch technology in china［J］.IEEE Trans.Magn，2003，39(1):39－41.

［2］李立毅，李小鹏.电磁发射的历史及发展趋势［J］.微电机，2004，37(1):41 －44.LI Li-yi，LI Xiao-peng.Electromagnetic emission history and development trend［J］.Micromotor，2004，37(1):41－44.

［3］王莹，肖峰.电炮原理［M］.北京:国防工业出版社，1995.WANG Yi，XIAO Feng.Elements of electrical gun［M］.Beijing:National Defense Industry Press，1995.

［4］MARSHALL R A，YING W.Railguns:their science and technology［M］.Beijing:China Machine Press，2004.

［5］GULLY J H.Power supply technoly for eleric guns［J］.IEEE Transactions onMagnetics，1991，27(1):329 －334.

［6］FAIR H D.Electromagnetic launch science and technology in the United States enters a new era［J］.IEEE.Trans.Magn，2005，41(1):158 －164.

［7］陈国庆，王永红，魏新劳，等.电容驱动型轨道炮电磁计算过程的计算机仿真［J］.电工技术学报，2006(4):68－71.CHEN Guo-qing，WANG Yong-hong，WEI Xin-lao，et al.Capacitance drive type rail gun electromagnetic calculation process computer simulation［J］.Transactions of China Electrotechnical Society，2006(4):68 －71.

［8］陈国庆，张海燕，王永红，等.电容器储能型轨道电磁炮的理论分析与动态仿真［J］.电机与控制学报，2008，44(5):435－437.CHEN Guo-qing，ZHANG Hai-yan，WANG Yong-hong，et al.The circuit theory analysis and dynamic simulation for the capacitor drived railgun［J］.Electric Machines and Control，2008，44(5):435－437.

［9］杨玉东，王建新.脉冲成型网络对轨道炮发射效率的影响［J］.火炮发射与控制学报，2011，46(4):41－45.YANG Yu-dong，WANG Jian-xin.Influnce of pulse forming network on rail gun launching efficiency)［J］.Journal of Gun Launch ＆ Control，2011，46(4):41 －45.

［10］谭赛，鲁军勇.电磁轨道炮的电磁参数特性研究及优化设计［J］.船电技术，2012，32(2):8 －12.TAN Sai， LU Jun-yong. The electric parameters characteristics and optimum design ofelectromagnetic railgun［J］.Marine Electric Technology，2012，32(2):8－12.

［11］周媛，严萍，袁伟群，等.电磁轨道发射装置中导轨几何参数对电感梯度的影响［J］.电工电能新技术，2009，28(3):23－27.ZHOU Yuan，YAN Ping，YUAN Wei-qun，et al.Effect of rail geometrical parameters on inductance gradient of EML［J］.Adv.ech.of Elec.Eng.＆ Energy，2009，28(3):23－27.

［12］巨兰，张碧雄.电磁轨道炮的炮体结构设计［J］.舰船科学技术，2011，33(7):94 －98.JU Lan，ZHANG Bi-xiong.Barrel structural design and research on electromagnetic railgun［J］.Ship Science and Technology，2011，33(7):94 －98.

［13］陶孟仙.电磁轨道炮固体电枢特性研究［D］.中国科学院等离子体物理研究所，1998.TAO Meng-xian.Electromagnetic railgun solid armature characteristic research［D］.Institute of Plasma Physics of Chinese Academy of Sciences，1998.

［14］MIGUEI D G.A 4.5－MJ pulsed power supply for railgun experiments［J］.IEEE Trans on Magnetics，2003，39(1):934 －938，280 －284.