先导式疏水阀阀芯组件动力特性分析

李树勋，胡建华，李连翠，徐晓刚，张 兴

(1.兰州理工大学石油化工学院，甘肃 兰州 730050;2.机械工业泵及特殊阀门工程研究中心，甘肃 兰州 730050)

针对国内高温高压凝结水回收工况需求，项目组研发了高温高压倒吊桶先导超大排量蒸汽疏水阀，其结构如图1所示.

蒸汽疏水阀主要由导阀、活塞组件、主阀、主阀阀芯、消声器、回复弹簧、高压管等部件组成［1-2］.该阀的设计条件:介质为蒸汽和凝结水;接管通径d=100 mm;最高工作压力p=8 MPa;最高工作温度t=296℃;热凝结水最大排量Q=30 t·h-1.采用抗水击性能好、承压能力高的倒吊桶先导式疏水阀作为导阀，即导阀本身就是一个先导式蒸汽疏水阀，由于其核心部件倒吊桶上开有排气孔，工作时桶内外的介质力可相互平衡，故可承受10 MPa以上的压力;主阀采用活塞与阀芯的一体化结构，主阀与导阀之间用高压管相连.

图1 倒吊桶先导式蒸汽疏水阀结构示意图

当管道中有凝结水产生时，凝结水经阀前高压管Ⅰ进入导阀内的倒吊桶中，倒吊桶下沉，小导阀开启，再带动导阀开启，凝结水、空气及不凝气体经导阀出口高压管Ⅱ进入活塞中，将阀前的介质压力引入活塞上腔，而活塞的截面积大于主阀阀芯的截面积，在相同的介质压力下，活塞向下作用力大于主阀芯向上的合力，此时活塞带动主阀芯向下运动，平稳打开主阀，凝结水迅速大量排放;当凝结水快排尽时，蒸汽逐渐充满倒吊桶上部并使其缓慢上升，小导阀关闭，紧接着导阀关闭，阻断活塞上腔介质补充，介质压力通过活塞上的泄压孔逐渐泄到疏水阀出口，此时主阀芯所受向上的弹簧力和介质力的合力大于活塞向下的介质作用力，活塞带动主阀芯平稳反向运动，关闭主阀，即完成一次排水过程［1］.由小导阀控制导阀，导阀控制主阀，巧妙的利用阀前介质力启闭主阀，从而获得大排量，实现阻汽通水排空气的功能.

在高温高压蒸汽凝结水系统中，先导式疏水阀启闭瞬间易发生压力脉动和空化现象，诱发剧烈振动，甚至引起阀内件及管线系统的破坏［3-4］.合作单位其他形式的先导式疏水阀在使用中发生过阀芯断裂的现象，裂口较平整，非汽蚀破坏造成，经分析是阀芯组件在低频振动下疲劳断裂.因此，需对新产品阀芯系统进行模态分析，为结构系统的振动特性分析、振动故障诊断及结构动态特性的优化提供依据［4］.

文中针对由主阀芯与活塞组成的阀芯组件，建立静态与预应力条件下的动力学方程，运用更为有效、计算占用内存小的顺序耦合法对考虑流固耦合与弹簧力的预应力的阀芯组件进行模态分析［5］，计算流固耦合和弹簧力的预应力条件下阀芯组件的前8阶固有频率和振型，并与静态条件下阀芯组件的振动特性进行比较分析.同时分析研究不同细长比、不同约束方式对阀芯组件模态的影响趋势.

1 计算模型及网格

以倒吊桶先导式蒸汽疏水阀内主阀芯与活塞组成的阀芯组件为研究对象，建立流固耦合几何模型如图2a所示，包括阀芯组件和阀腔流道.

将此模型导入ANSYS/Workbench进行前处理，分别对阀芯组件和阀腔流道进行网格划分.阀芯组件网格如图2b所示，阀腔流道网格如图2c所示.

2 数学模型

2.1 阀芯组件模态数学模型

忽略流固耦合作用力及弹簧力时，阀芯组件的动态振动问题可看作是作用在阀芯组件上的激励力引起的受迫振动.振动方程为［5-7］

式中:M为结构质量矩阵;C为结构阻尼矩阵;K为结构刚度矩阵;F(t)为载荷向量;δ为各节点位移向量.

忽略外力作用，即F(t)=0，由于实际工程结构中，阻尼对结构固有特性的影响较小，通常可忽略不计，则式(1)可简化为自由振动方程，即

对式(2)进行求解变换可以得到固有频率ω的2n次代数方程式:

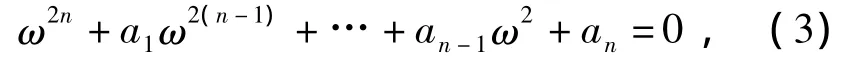
由式(3)可以求得结构各阶固有振动频率ωi及振型.

2.2 阀芯组件预应力模态数学模型

高温高压倒吊桶先导式蒸汽疏水阀工作过程中，阀芯组件受到流体作用力及弹簧回复力等载荷作用.此时阀芯组件的模态分析数学模型如下:

式中:PC为载荷向量;MC为载荷质量阻尼矩阵.

3 考虑流固耦合和弹簧力的预应力模态分析

对于流固耦合作用导致的不均匀流动动力场，通过Workbench/Fluid Flow(FLUENT)进行模拟计算.在Fluid Flow中，导入流固耦合模型，抑制阀芯结构;以连续性方程、三维雷诺平均N-S方程和基于各向同性涡黏性理论的双方程组成疏水阀内部流动数值模拟的控制方程组，采用有限体积法对控制方程组进行离散;本次计算的进口处边界条件为压力进口，出口处为压力出口［8］.流场的压力分布与速度分布如图3所示.

插入结构静态分析，将CFD计算的结果作为初始边界条件，并设定阀芯组件上的弹簧作用力，进行流固耦合应力分析［5，9］.耦合预应力分布如图 4所示，阀杆上的最大应力小于材料的许用应力，所以阀杆强度满足要求.

图3 流场分析结果

图4 阀芯组件预应力分布

将获得的阀芯表面应力分布作为模态分析边界条件，施加一端固定一端轴向自由的约束，进行预应力模态分析［10-12］.模态分析频率结果如表1所示.其对应的阀芯前8阶模态的振型如图5、图6所示.

表1 阀芯组件静态模态及预应力模态固有频率和振型最大值及结果对比

由表1可以看出，在预应力影响下，阀芯组件第6阶固有频率有所增大，其余固有频率有所减小，说明在流场与弹簧力预应力的作用下，阀芯组件的动力学特性发生了改变，产生了一定的预应力效应［12］.从频率差异率可以看出，流固耦合对前3阶频率影响比对第4阶及以后阶次的频率影响大，但总体上阀芯组件静态模态固有频率与预应力模态固有频率在数值上相差不大，说明流固耦合场与弹簧预应力对阀芯组件固有频率影响较小.

图5 阀芯组件预应力模态分析前8阶振型图

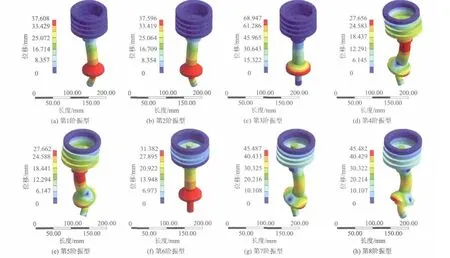
图6 阀芯组件静态模态分析前8阶振型图

由表1还可以看出，在考虑预应力之后，最大振型位移较未考虑之前有所增加，但在数值上增加不大，其中第4阶振型最大值增大了22.4%.在第3阶时，最大振型位移达到最大.从图5，6可以看出，静态条件和考虑流固耦合与弹簧力预应力条件下阀芯组件前3阶振型主要表现均为主阀芯的振动，活塞组件振型基本为0，其余阶振型的主阀芯和活塞组件均发生振动.1，2，4，5，7，8 阶振型均表现为阀芯组件径向的振动，其余阶振型均表现为轴向的振动，最大振型位移位置基本一致.考虑预应力影响后，阀芯组件第2，5，7，8阶振型方向发生变化，其余几阶振型方向基本一致，但阀芯组件总体振型表现形式变化不大.

4 阀芯不同细长比模态计算及分析

对不同细长比的阀芯进行三维建模，并进行模态分析，以探讨阀芯直径变化对阀芯组件模态频率及振型的影响.

阀芯的细长比(即柔度)按下式计算:

式中:dF为阀芯直径;lF为阀芯长度;μλ为长度系数，此处取0.699.

从图7a，b可以看出，随着阀芯细长比的增加，阀芯组件的模态频率呈逐渐降低，最大振型位移呈逐渐增加的趋势，这说明阀芯直径越大，阀芯组件模态频率越大，最大振型位移越小.这主要是因为阀芯直径的增加相应地增大了阀芯组件的刚度，使阀芯的固有频率增高.由图7b可知，不同细长比的阀芯组件都在第3阶时，最大振型位移达到最大，随后有所减小，且最大振型位移的变化规律一致.

图7 不同细长比前8阶频率振型曲线图与不同约束前8阶频率曲线图

5 阀芯组件不同约束模态计算分析

约束条件对结构固有频率和振型的影响比较大，分别对阀芯组件分别施加一端固定一端自由、一端固定一端轴向自由、两端固定约束，并进行模态分析［13］.图7c中A为一端固定一端自由约束，B为一端固定一端轴向自由约束，C为两端固定约束.从图7c中可以看出，通过对3种约束方式的比较仿真，可以看出采用两端固定约束时，阀芯组件固有频率最大，最大振型位移最小;一端固定一端自由时固有频率最小，最大振型位移最大.从模态振型图6，8，9可知，施加不同约束，振型变化较大.从图7a，c可以看出，改变约束方式固有频率变化幅度比增加阀芯直径大.因此，改变阀芯组件约束方式，在阀芯组件形状没有改变、重量没有增加的情况下，提高了阀芯组件的固有频率，降低了最大振型位移，使整个系统刚度得到了提高，说明改进高温高压倒吊桶先导式蒸汽疏水阀阀芯组件的安装方式是有意义的.

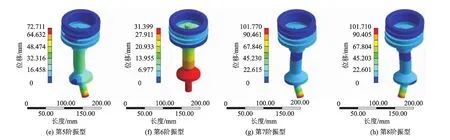
图8 施加一端固定一端自由约束前8阶振型图

图9 施加两端约束前8阶振型图

6 结论

1)阀芯组件在流固耦合和弹簧力的预应力作用下固有频率和振型均有变化，但变化不大，表明流体作用力、弹簧力等载荷对本阀芯组件的动力学特性发生了改变，产生了一定的预应力效应，但影响较小.

2)随着阀芯组件细长比的增加，模态频率呈逐渐降低，最大振型位移呈逐渐增加的趋势，表明阀芯直径越大，组件模态频率越大，最大振型位移越小.

3)通过对3种约束方式的比较，可以看出采用两端固定约束时，阀芯组件固有频率最大，最大振型位移最小;采用一端固定一端自由时固有频率最小，最大振型位移最大.采用不同约束方式，振型变化较大.改变阀芯组件的约束方式，固有频率变化幅度比增加阀芯直径大.

4)疏水阀阀芯断裂前，采用的约束方式为一端固定一端自由，现改进为一端固定一端轴向自由的安装方式，在不改变尺寸、材质等的情况下，提高了系统的刚度，有效防止阀芯的断裂，提高整个结构系统动态特性及稳定性.

References)

［1］李树勋，徐登伟，李 确，等.倒吊桶先导式蒸汽疏水阀的设计与数值模拟［J］.排灌机械工程学报，2012，30(3):99-103.Li Shuxun，Xu Dengwei，Li Que，et al.Design and numerical simulation of inverted bucket pilot-operated steam trap ［J］.Journal of Drainage and Irrigation Machinery Engineering，2012，30(3):99-103.(in Chinese)

［2］李树勋，王结勤，张云龙，等.一种新型倒吊桶可调先导超大排量蒸汽疏水阀:中国，201010563217.5［P］.2011-04-06.

［3］李树勋，赵子琴，张云龙.高温高压过热蒸汽疏水阀消声减振研究［J］.振动与冲击，2011，30(10):116-121.Li Shuxun，Zhao Ziqin，Zhang Yunlong.Noise elimination and vibration reduction for a superheat steam trap with high temperature and high pressure［J］.Journal of Vibration and Shock，2011，30(10):116-121.(in Chinese)

［4］屠 珊，孙 弼，毛靖儒.气流诱发调节阀杆振动的研究［J］.动力工程，2004，24(5):729-731.Tu Shan，Sun Bi，Mao Jingru.Experimental research on oscillation induced by fluid flow in control valve［J］.Power Energy，2004，24(5):729-731.(in Chinese)

［5］陈向阳，袁丹青，杨敏官，等.基于流固耦合方法的300 MWe级反应堆主泵叶片应力分析［J］.机械工程学报，2010，46(4):111-115.Chen Xiangyang，Yuan Danqing，Yang Minguan，et al.Blade stress of the reactor coolant pump of 300 MWe nuclear power plant in China based on fluid-solid coupling method［J］.Journal of Mechanical Engineering，2010，46(4):111-115.(in Chinese)

［6］Firouz-Abadi R D，Noorian M A，Haddadpour H.A fluid-structure interaction model for stability analysis of shells conveying fluid［J］.Journal of Fluids and Structures，2010，26:747-763.

［7］Zhang R J，Wang W Q，Hou S H，et al.Modal analysis for beam bundle in fluid ［J］.Journal of Pressure Vessel Technology，2002，124:223-228.

［8］Zhang Li，Luo Jing，Yuan Ruibo，et al.The CFD analysis of twin flapper-nozzle valve in pure water hydraulic［J］.Procedia Engineering，2012，31:220-227.

［9］Shi Nietao，Ju Jinsan，You Xiaochuan，et al.Dynamic buckling analysis on fluid-solid coupling of large liquid storage tank ［J］.Sensor Letters，2012，10:131-137.

［10］Liu Demin，Liu Xiaobing.Vibration analysis of turbine based on fluid-structure coupling［J］.Chinese Journal of Mechanical Engineering，2008，21(4):40-43.

［11］Jean-François Sigrist，Daniel Broc，Christian Lainé.Fluid-structure interaction effects modeling for the modal analysis of a nuclear pressure vessel［J］.Journal of Pressure Vessel Technology，2007，129:1-6.

［12］谢远森，李意民，周忠宁，等.旋转预应力条件下的叶片流固耦合模态分析［J］.噪声与振动控制，2009(4):34-37.Xie Yuansen，Li Yimin，Zhou Zhongning，et al.Mode analysis of fluid-structure coupling blade under rotational and pre-stress condition［J］.Noise and Vibration control，2009(4):34-37.(in Chinese)

［13］Larbi W，Deü J F，Ohayon R.Vibration of axisymmetric composite piezoelectric shells coupled with internal fluid［J］.International Journal for Numerical Methods in Engineering，2007，71(12):1412-1435.