半主动空气悬架多模式切换控制模型的分析

汪少华，陈 龙，孙晓强

(江苏大学汽车与交通工程学院，江苏 镇江 212013)

悬架是车辆底盘系统中的重要部件，对车辆动态性能具有重大影响，因此，提高悬架系统的性能具有重要的工程意义［1－2］.与传统被动悬架相比，半主动空气悬架不仅能够实现阻尼自适应调节，而且能对车身高度进行主动控制，因而对于改善车辆在行驶过程中的乘坐舒适性、行驶安全性以及燃油经济性都具有重要作用，已成为汽车工程界的研究热点［3－4］.

随着空气弹簧和可调阻尼减振器研究的日益成熟，控制系统的设计已成为实现半主动空气悬架控制功能要求、提高半主动空气悬架自适应能力的关键.对此，国内外学者开展了大量的研究工作，提出了多种针对半主动空气悬架的控制策略和控制方法.例如，王辉等［5］将自适应神经网络运用到半主动空气悬架系统的控制之中，取得了较好的效果.C.Graf等［6］基于天棚阻尼控制理论对半主动空气悬架的阻尼力进行了控制，改善了车辆乘坐舒适性.H.Kim等［7］对空气悬架的高度进行了滑模自适应控制，并通过仿真和实车试验，验证了所设计的控制系统的有效性.

然而，综合相关研究成果可以发现，相关研究主要集中在针对半主动空气悬架局部控制目标进行控制系统设计，虽然达到了所需的控制效果，但是忽略了半主动空气悬架在控制过程中存在的高度与阻尼协调控制的问题.近年来，部分学者意识到这个问题，他们根据实车运行工况设计了电控空气悬架高度和阻尼控制模式，同时制定了相应的模式控制策略，初步实现了空气悬架与整车性能的良好匹配，但是没有对模式切换控制系统进行详细设计，也没有对模式间切换参数进行深入研究［8－9］.

针对上述问题，笔者结合车辆实际行驶工况，提出将半主动空气悬架控制过程分解为高度和阻尼多种控制模式，同时基于车身高度切换优先的控制原则将车身高度控制和阻尼自适应调节解耦，采用逻辑判断方法制定各模式间的切换规则.根据车辆燃油经济性和行驶通过性，确定各模式间的主要切换参数，在此基础上，基于Simulink/Stateflow进行切换控制系统的建模和仿真，验证所设计的切换控制系统的实际性能.

1 半主动空气悬架控制模式

1.1 高度控制模式

车身高度的调节主要是以提高车辆的通过性、操稳性以及燃油经济性为目的.为了得到最佳的悬架性能，空气悬架系统根据车速和路况变化自动调节车身目标高度.根据车辆实际行驶状况，确定高度模式的切换依据主要为车速和路面，车身高度分高位、中位和低位3种模式.为了防止在短时间内出现多次车身高度的切换，增加了持续时间这一判定条件，以提高车身高度调节的稳定性.车身高度控制策略如图1所示.

图1 车身高度控制策略

出于安全原因，转向工况下车辆不能进行底盘高度切换.因此，上述高度控制模式是针对车辆直线行驶工况提出的，若系统识别出车辆处于转向工况，车身高度将不进行调节.

1.2 阻尼控制模式

由于空气弹簧高度与刚度的耦合，随着车身高度的调节，空气弹簧的刚度会随之改变，同时路面状况、车速以及载荷也会发生实时变化，因此，半主动空气悬架的阻尼控制需要考虑2个方面:①与空气弹簧刚度的匹配;②控制目标的实时变化.例如，在车身高位模式下，路面较差，此时阻尼控制目标为提高乘坐舒适性，而在车身低位模式下，由于车速较高，行驶安全性显得更为重要，转向工况下，自然是以提高车辆操稳性为首要目标.

因此，结合半主动空气悬架高度和阻尼的控制特点，确定阻尼控制模式为4种:① 车身高位下的阻尼控制;②车身中位下的阻尼控制;③ 车身低位下的阻尼控制;④ 转向工况下的阻尼控制.针对车身高度控制与阻尼控制之间的耦合问题，提出基于高度调节优先的高度和阻尼协调控制机制，通过先进行高度调节再进行阻尼控制，以此实现高度和阻尼控制的解耦.综上所述，半主动空气悬架高度与阻尼协调控制过程如图2所示.

图2 半主动空气悬架高度与阻尼协调控制过程

2 多模式切换控制描述

2.1 控制模式及模式切换过程的描述

根据切换系统理论，控制模式的切换可以用有向图C={M，E}来表示，其中:M为控制模式的集合;E={e=(i，j):mi，mj∈M}为控制模式变迁(离散事件)的集合，e=(i，j)表示使控制模式mi变迁到mj的离散事件.

根据半主动空气悬架高度与阻尼的实际调节过程，半主动空气悬架的控制模式分为

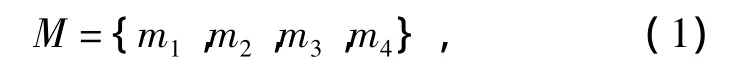
式中:m1，m2，m3分别为直线行驶工况下的车身低位、中位和高位控制模式;m4为转向工况模式.

控制模式的切换过程描述如下:在初始时刻t0时，控制模式为mi，在离散事件e=(i，j)发生之前，(x)=f(x，m，t);t，遵循连续动态行为ii在1时刻离散事件e=(i，j)发生，控制模式变迁为mj，即离散事件e=(i，j)的发生导致控制模式从mi变迁为mj，此后系统将遵循新控制模式下的连续动态行为(x)=fj(x，mj，t).因此，控制模式的切换过程可用图3表示.

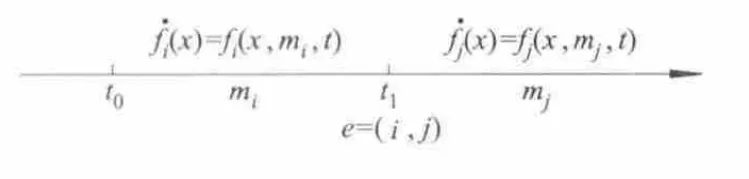
图3 控制模式的切换过程

2.2 模式切换规则的描述

控制模式的切换规则采用逻辑判断方法，通过判断一系列离散事件是否发生来决定系统应工作在哪种控制模式［10］.具体切换规则如下:

1)当前轮转角δ大于转向工况下的临界转角δ0，系统判定此时车辆处于转向工况下，系统进入转向工况控制模式m4;当前轮转角δ小于转向工况下的临界转角δ0，系统判定此时车辆处于直线行驶工况，系统进入直线行驶工况下的系统控制.

2)当车辆行驶速度v达到进入车身低位模式下的临界速度v1，且持续时间t大于判定时间th，系统判定车辆是以较高的速度行驶在良好路面上，为了提高车辆燃油经济性和操纵稳定性，车身降低一定高度，进入车身低位控制模式m1.

3)当车辆行驶速度v低于临界速度v1，同时悬架动行程fd的均方根值RMSfd小于较差路面的最低均方根值RMSfd0，且持续时间t大于th，系统判定车辆是以中等速度行驶在较好的路面上，为了提高此工况下的车辆综合性能，进入车身中位控制模式m2.

4)当悬架动行程fd的均方根值大于较差路面的最低均方根值RMSfd0，且持续时间t大于th，系统判定车辆是以较低的速度行驶在较差的路面上，为了提高车辆通过性，车身升高一定的高度，进入车身高位控制模式m3.

根据上述切换规则，可以列出如表1所示的系统控制模式切换时所用到的逻辑判断值.

表1 控制模式切换时的逻辑判断值

结合4种控制模式及所设计的切换规则，半主动空气悬架的整体模式切换控制过程可用图4表示，系统默认的初始状态为车身中位模式，系统启动后便根据实际的行驶工况进行控制模式的最优实时调整.

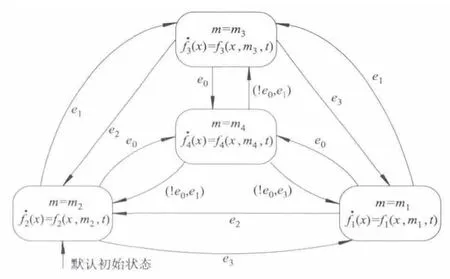
图4 半主动空气悬架的整体模式切换过程

3 切换参数的确定

切换参数的确定是否合理直接影响所设计的控制系统对车辆实际运行工况的跟踪性能，目前，针对这一问题的研究相对较少.笔者考虑通过结合车身高度的调节目标以及车辆行驶动态性能，对进入车辆低位模式的临界车速以及进入车身高位模式的临界路面进行研究.

3.1 进入车身低位模式的临界车速

当车辆高速行驶时，空气阻力急剧增加，为了提高操纵稳定性，降低风阻，装有空气悬架的车辆可通过对空气弹簧进行放气来降低车身高度.

在汽车正常行驶工况下，空气阻力Fw是与气流相对速度的动压力成正比，即

式中:CD为空气阻力系数;ρ为空气密度，ρ=1.2258 N·s2·m－4;A为迎风面积，即汽车行驶方向的投影面积.

只讨论无风条件下的汽车运动，所以vr即为汽车行驶速度va，va的计量单位以km·h－1，A的计量单位以m2计，则空气阻力可表示为

除了空气阻力，汽车所受的行驶阻力主要为滚动阻力，滚动阻力Fμ可表示为滚动阻力系数μ与车轮负荷W的乘积，即

式中:车轮负荷比较容易确定，而滚动阻力系数与路面的种类、行驶车速以及轮胎的构造、材料、气压等有关，采用下面的经验公式估算［11］:

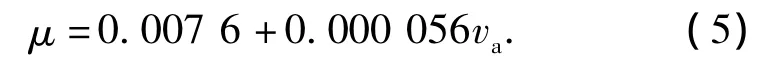
所以滚动阻力可以表达为

以某高级轿车为例，利用数值仿真定量解析滚动阻力与空气阻力随车速的变化趋势以及二者之间的关系.该车参数:W=18000 N;CD=0.3;A=2 m2.仿真结果如图5所示.

图5 空气阻力与滚动阻力间的关系

从图5可以看出，当车速为90 km·h－1时，空气阻力逐渐增大到与滚动阻力相当，随着车速的继续增加，空气阻力将超过滚动阻力并以较快的速度继续增长.当车辆在空气阻力和滚动阻力大致相当的速度下降低车身高度，既不会影响车辆的通过性，同时可以有效降低风阻，提高车辆的燃油经济性和操纵稳定性.因此，确定进入车身低位控制模式的临界车速为90 km·h－1.

3.2 进入车身高位模式的临界路面

路面的好坏是影响车身高度切换的另一个重要依据，路面好坏对车辆最直接的影响之一就是悬架动行程，同时由于悬架动行程只是车辆垂向运动的一个性能评价指标，因此只需建立车辆1/4悬架模型，如图6所示，便可探究悬架动行程与路面的直接关系.

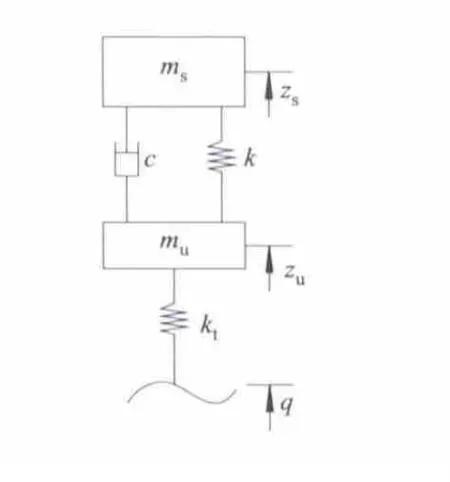
图6 车辆悬架1/4模型

根据牛顿力学，得到系统动力学方程为

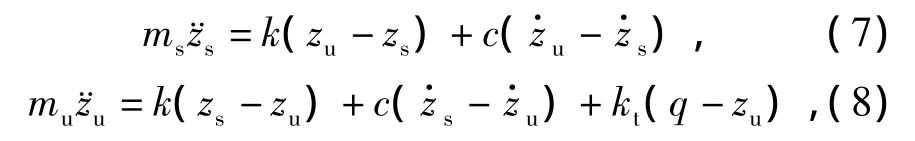
式中:ms为簧载质量;zs为簧载质量垂直位移;mu为非簧载质量;zu为非簧载质量垂直位移;k为悬架弹簧刚度;c为悬架阻尼系数;kt为轮胎刚度;q为路面垂直振动输入.

在Matlab/Simulink中建立仿真模型，以前文分析空气阻力与滚动阻力关系的同一型轿车为例，相关参数:ms=450 kg;mu=60 kg;k=15 kN·m－1;c=1460 N·s·m－1;kt=192000 N·m－1.车辆正常行驶的路面大多在D级以上，因此，对于车辆需要提升底盘高度的路面，可以认为其等级在E级及E级以下，如车辆处于越野工况，所以仿真采用的路面输入分别为C级和E级路面，车速为36 km·h－1，仿真结果如图7所示.

图7 悬架动行程仿真结果

从图7可以看出，车辆行驶在E级路面上的悬架动行程绝对值要明显高于C级路面，通过进一步计算可得，E级路面上悬架动行程均方根值为0.035，而C级路面上为0.009，由此确定表征该车辆进入车身高位模式的临界路面的悬架动行程均方根值为0.035.即当悬架动行程均方根值大于0.035时，系统判定此时车辆可以进入车身高位控制模式.

4 切换控制系统的建模与仿真

4.1 切换控制系统建模

通过对半主动空气悬架实际运行工况进行分析，确定了半主动空气悬架的控制模式及控制规则，同时进行了模式间主要切换参数的确定，在此基础上，为了构造一个能够满足半主动空气悬架模式动态切换的控制系统，建立了基于多模式切换的半主动空气悬架控制模型，如图8所示.

图8 半主动空气悬架多模式切换控制模型

切换控制系统通过Simulink/Stateflow进行建模，在半主动空气悬架多模式切换控制系统中，实际输入与系统输入的关系如表2所示，系统输出与控制器的选择关系如表3所示.

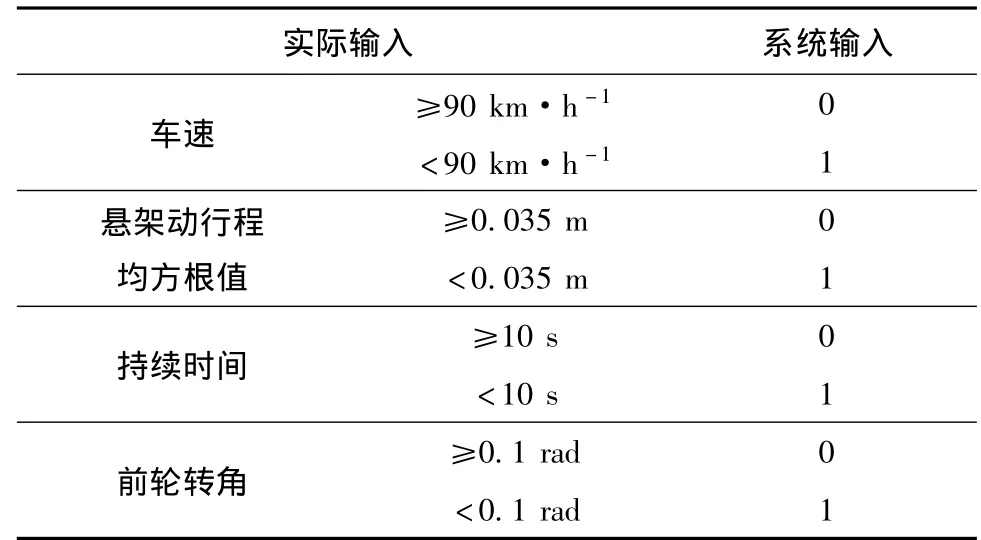
表2 实际输入与系统输入关系

表3 系统输出与控制器的选择关系

根据表2，3所示的系统工作变量关系，设计出切换控制系统的Stateflow模型如图9所示.

图9 切换控制系统Stateflow模型

4.2 切换控制系统的仿真

为了验证所建立的半主动空气悬架切换控制系统的准确性和有效性，将如图10所示的前轮转角信号、车速信号、悬架动行程信号以及相应的工况变化持续时间信号作为切换控制系统的输入，系统经仿真得到的输出信号如图11所示.

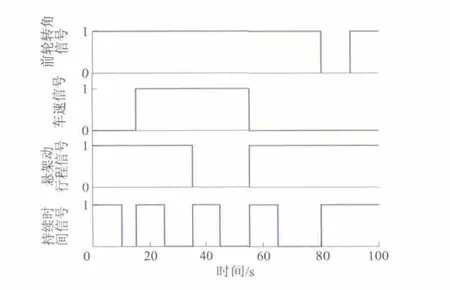
图10 系统输入信号

图11 系统输出信号

从图10，11可以看出，基于 Simulink/Stateflow建立的半主动空气悬架切换控制系统能够准确地根据相应的输入信号进行控制模式的切换.例如，当车速输入信号为0，悬架动行程信号为1，持续时间信号为0，前轮转角信号为1时，表明车辆是以较高的车速直线行驶在良好的路面上，系统应进入车身低位控制模式，此时控制输出结果为control=1，control1=2，系统选择车身低位控制器，符合控制要求.

5 结论

1)提出了符合车辆实际运行工况的车身高度和阻尼控制模式和控制策略，基于逻辑判断方法制定了模式间切换控制规则.

2)针对车身高度控制和阻尼自适应调节之间的耦合问题，提出了基于车身高度切换优先的控制原则，实现了二者之间的解耦.

3)基于Simulink/Stateflow进行了切换控制系统实际性能的仿真，仿真结果表明:所设计的多模式切换控制系统符合系统控制要求，下一步将在有效的切换控制系统基础上进行局部控制器的设计.

References)

［1］Fischer D，Isermann R.Mechatronic semi-active and active vehicle suspensions［J］.Control Engineering Practice，2004，12:1353 －1367.

［2］Zehsaz M，Sadeghi M H，Ettefagh M M，et al.Tractor cabin's passive suspension parameters optimization via experimental and numerical methods［J］.Journal of Terramechanics，2011，48:439 －450.

［3］Holtz M W，van Niekerk J L.Modeling and design of a novel air spring for a suspension seat［J］.Journal of Sound and Vibration，2010，329:4354 －4366.

［4］Kim H，Lee H.Fault-tolerant control algorithm for a four-corner closed-loop air suspension system［J］.IEEE Transactions on Industrial Electronics，2011，58(10):4866－4879.

［5］王 辉，朱思洪.半主动空气悬架神经网络的自适应控制［J］.农业机械学报，2006，37(1):28－31.Wang Hui，Zhu Sihong.Neural network adaptive control for semi-active air suspension［J］.Transactions of the Chinese Society for Agricultural Machinery，2006，37(1):28 －31.(in Chinese)

［6］Graf C，Maas J.Commercial vehicle cabin with active air suspension for improved ride comfort［C］∥IEEE/ASME International Conference on Advanced Intelligent Mechatronics.Piscataway:IEEE，2011:259 －264.

［7］Kim H，Lee H.Height and leveling control of automotive air suspension system using sliding mode approach［J］.IEEE Transactions on Vehicular Technology，2011，60(5):2027－2041.

［8］江 洪，李 坤，周文涛，等.ECAS系统控制模式及控制策略［J］.机械工程学报，2009，45(12):224－231.Jiang Hong，Li Kun，Zhou Wentao，et al.Control mode and control strategy in ECAS system［J］.Journal of Mechanical Engineering，2009，45(12):224 － 231.(in Chinese)

［9］汪若尘，张孝良，陈 龙，等.车身高度与可调阻尼集成控制系统［J］.农业工程学报，2012，28(11):75 －79.Wang Ruochen，Zhang Xiaoliang，Chen Long，et al.Integrated control system of vehicle body height and adjustable damping［J］.Transactions of the Chinese Society of Agricultural Engineering，2012，28(11):75 － 79.(in Chinese)

［10］胡春华，何 仁，李 楠.基于切换系统的HEV能量控制系统优化设计［J］.江苏大学学报:自然科学版，2011，32(5):497 －501.Hu Chunhua，He Ren，Li Nan.Optimal design of energy control system of HEV based on switched system［J］.Journal of Jiangsu University:Natural Science Edition，2011，32(5):497 －501.(in Chinese)

［11］余志生.汽车理论［M］.5版.北京:机械工业出版社，2010.