基于QFD技术的船舶设计决策方法

熊云峰，陈章兰，袁红莉

(集美大学轮机工程学院，福建 厦门 361021)

0 引言

满足船东需求是船舶设计工作的根本出发点，也是最终落脚点。“顾客 (船东)至上”是船舶设计者必须践行的设计理念。所以，在开展船舶设计时，特别是在进行船舶设计方案决策时，必须从满足船东的需求出发，从众多可行方案中选择出符合船东需求的最佳方案。而要实现这一目标，最有效的手段就是在进行设计决策时，要高度重视船东需求在船舶设计过程中的基础性作用，进而建立恰当的决策分析模型，以使决策过程能充分体现“船东至上”的设计原则。

质量功能配置 (quality function deployment，QFD)是顾客驱动的产品设计方法，强调用户需求在产品设计过程中的基础性作用，是系统工程思想在产品设计过程中的具体应用，其目标是在产品设计阶段实现顾客满意。QFD技术的运用主要通过构建质量屋的方式来完成［1-5］。QFD技术目前在船舶设计决策领域还没有公开的应用成果，但在其他产品设计中有很多成功的应用案例，如文献 ［1-5］等。

基于此，本文针对船舶设计方案决策问题的特点，尝试将QFD技术应用到船舶设计决策工作中来，利用QFD技术建立船舶设计决策质量屋，提出一种基于QFD技术的船舶设计决策方法，以实现对船舶设计方案进行科学的系统决策。

1 基于QFD技术的船舶设计决策思路与步骤

1.1 基本思路

基于QFD的船舶设计决策思路与流程如图1所示。

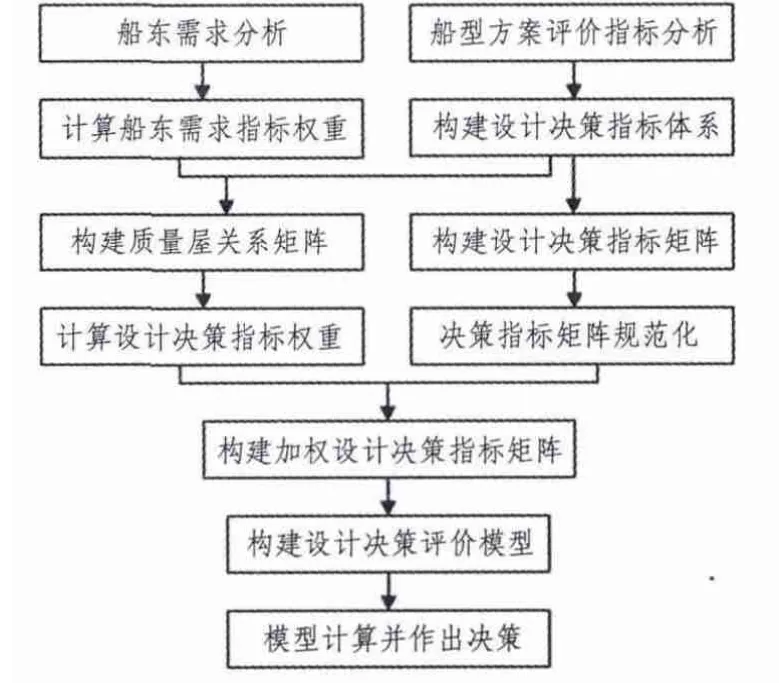
图1 船舶设计决策思路与流程Fig.1 The idea and process of the decision-making of ship design

1.2 具体步骤

1)船东需求分析并计算需求的权重

运用专家座谈、船东访谈、调查研究等方法，确定船东的具体需求(设有n个需求，以xi表示，i=1，2，…，n)，然后运用层次分析法计算出船东需求的权重矩阵 α=［αi］1×n。

2)构建船舶设计决策指标体系

根据船型方案的特点，从众多影响船舶设计质量特性的因素中挑选出具有代表性的质量特性指标(设代表性的指标有m个，以yj表示，j=1，2，…，m)，建立船舶设计决策的指标体系。

3)构建质量屋关系矩阵

首先，分析船东需求与设计决策指标之间关联程度，并以相应的具体数值表示二者之间的关联程度［2］(如表1所示)，构造船东需求与决策指标之间的关联关系矩阵 A=［αij］n×m。

表1 船东需求与设计决策指标之间关联程度的对应数值Tab.1 The corresponding data of the relevance between the decision-making index and shipowner requirement

然后，逐一分析船舶设计决策指标之间的相关关系，并以相应的具体数值表示二者之间的关联程度［2］(如表2所示)，且将某一决策指标与其自身的自相关关系定义为1，则可构造决策指标之间的自相关矩阵 B=［bij］m×n。

表2 设计决策指标之间关联程度的对应数值Tab.2 The corresponding data of the relevance between the decision-making index and the decision-making index

在具体构建关系矩阵的过程中，为了提高所构建关系矩阵的准确性，可请若干专家按上述方法参与评价并给出具体的数值，然后进行算数平均得到相应的最终关联数值。例如，若有10位专家给出某一船东需求与某一决策指标之间的关联数值总和为12，则二者最终的关联数值就为1.2。

4)计算设计决策指标权重向量ω

首先，根据矩阵A和B按式(1)可得到修正后的关联矩阵C:

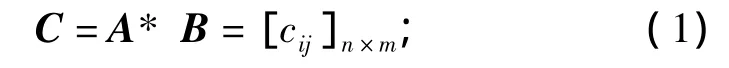
然后，按式(2)可计算出船舶设计决策指标权重矩阵β，

最后，对β进行归一化处理，得设计决策指标权重向量 ω［3］，

5)构造决策指标矩阵i

设有s个决策对象(船型方案)，每个决策对象有m个决策指标，则有决策对象集合U=［Uk］，决策指标集合V=［Vj］，djk表示第k个决策对象Uk的第 j个评价指标 Vj的值(j=1，2，…，m;k=1，2，…，s)，则决策指标矩阵 D=［djk］m×s。

6)规范化决策指标矩阵

由于决策指标的物理意义不同，导致相互之间通常具有不同的量纲，而且数值的数量级相差悬殊。因此，为了消除评判指标对方案决策带来的不利影响，需对数据进行规范化处理。处理方法为:

经规范化处理后决策指标矩阵

7)构建加权决策指标矩阵

式中:fjk= ωj× ejk，(j=1，2，…，m;k=1，2，…，s)。

8)综合设计决策

在对指标值无量纲化后，就可以将信息熵原理中的“指标”看作是“方案”、 “方案”看作是“指标”，这样处理后，最后求得的“指标”熵值实质就是方案的重要度。因此，可以应用信息熵原理，构建如式(7)所示的综合决策模型［6-7］:

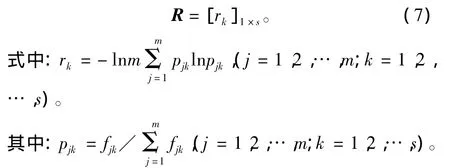
根据向量R，可作出决策:R中rk的值越大，表明所对应的决策对象的综合性能越好;R中rk的值越小，表明所对应决策对象的综合性能越差。即rk值大者为优，rk值小者为劣。

2 方法应用

1)QFD团队根据上述步骤1确定质量屋中的顾客需求分别为:适用性好(x1)、经济性好(x2)、安全可靠(x3)、先进美观(x4)4项需求;

2)QFD团队根据上述步骤1确定质量屋中的决策指标有:航速(y1)、稳性(y2)、耐波性指数(y3)、操纵性(y4)、净现值(y5)、必要运费率(y6)、船舶造价(y7)、噪声指数(y8)、船型成熟度(y9)等9项。

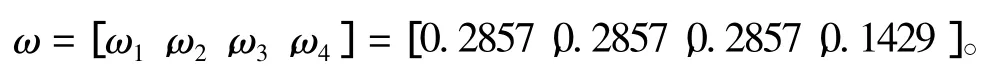
运用层次分析法［6］，获取顾客需求的权重向量:3)QFD团队根据上述步骤3，确定船东需求与设计指标之间的关联关系矩阵、设计指标之间的自相关矩阵(如表3所示)。然后，按式(1)～式(3)计算可得设计决策指标的权重(具体结果见表3中的最后一行)。

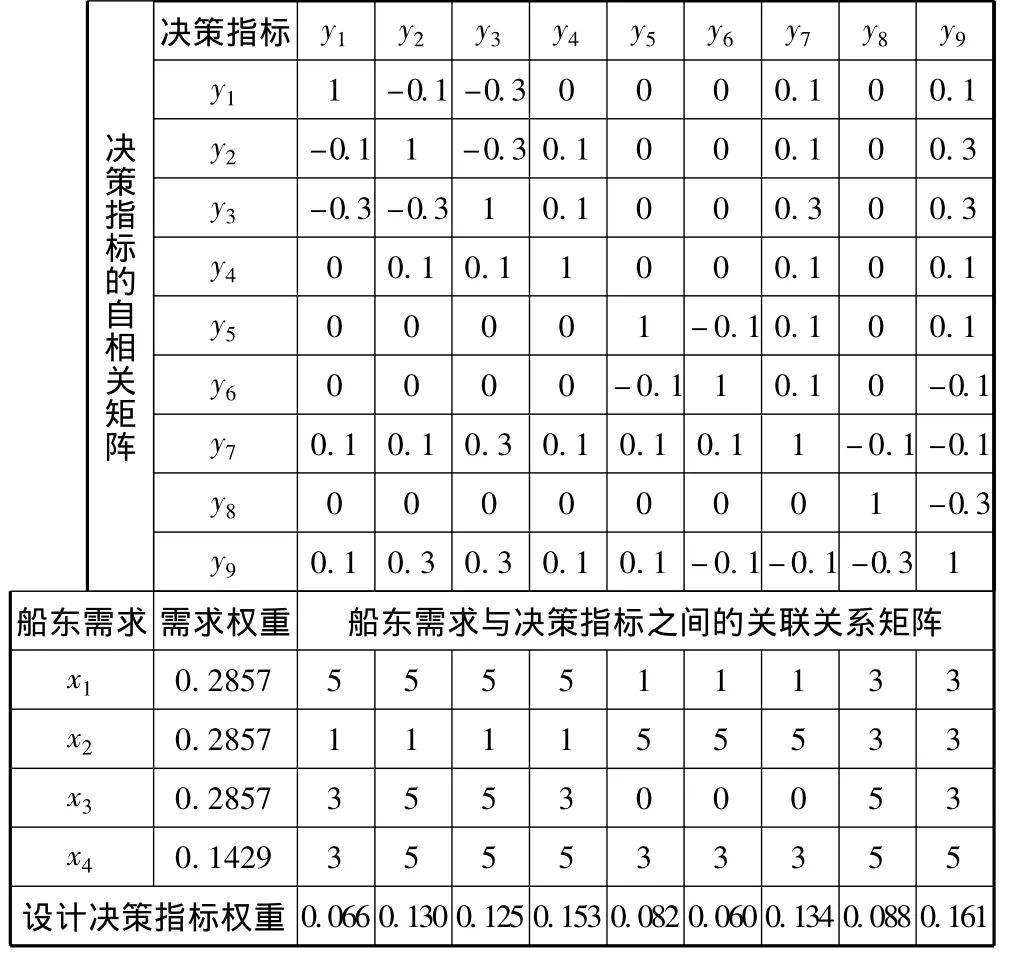
表3 船舶设计决策质量屋Tab.3 The house of quality of the decision-making of ship design

4)船舶设计决策

以4艘油船设计方案为决策对象，其9项决策指标值如表4 所示［8］。

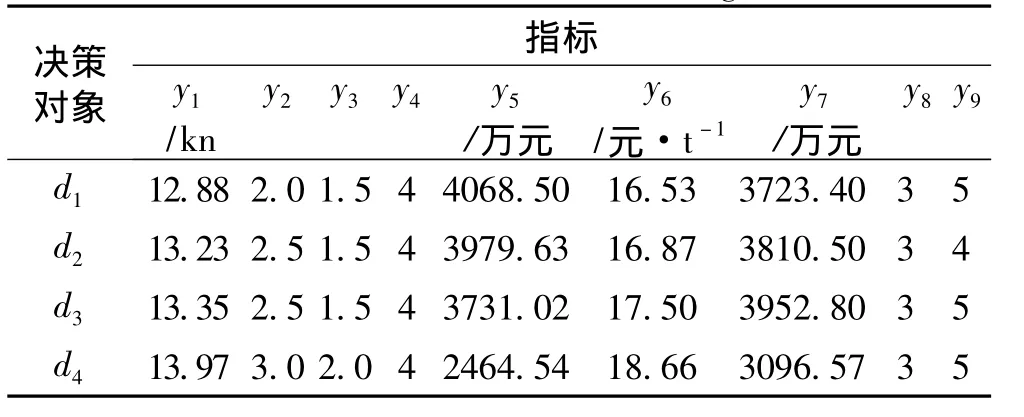
表4 四艘油船设计方案的决策指标值Tab.4 The data of the decision-making index

根据上述步骤5～步骤7，可得决策指标矩阵D、规范化决策指标矩阵E及加权决策指标矩阵F:

然后，按式(7)计算可得

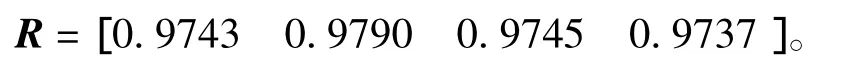
比较R中各元素的大小，得到船型方案的排序结果为:d2＞d3＞d1＞d4，最优船型方案为方案2。

3 结语

本文运用QFD技术和信息熵原理，建立了一种新的船舶设计决策方法。该方法具有以下特点:

1)将QFD技术应用到船舶设计决策工作中来，利用QFD技术建立船舶设计决策质量屋，进而计算出了船舶设计决策指标的权重，使所得的权重充分地反映了船舶的需求作用，使决策过程充分体现了“船东至上”的设计理念。

2)运用信息熵原理，建立了基于QFD技术的船舶设计决策模型，很好地处理了多指标、多目标综合评价问题。该方法计算过程简单、实用性强。

3)虽然本文所举的算例较为简单，但本文所提的方法可以很容易推广应用到其他更为复杂的多目标、多指标的船舶设计决策、船舶投资决策等决策工作中去，所不同的是仅仅增加了计算工作量。

虽然本文作了一些有益的探索，但所建立的船舶设计决策方法的科学性与实用性有待进一步研究，更有待实践的进一步检验，这也是今后努力钻研的方向。

［1］熊伟，王娟丽，蔡铭.基于QFD技术的软件可信性评估研究［J］.计算机应用研究，2010，27(8):2991-2994.XIONG Wei，WANG Juan-li，CAIMing.Trustworthy software evaluation based on QFD ［J］.Application Research of Computers，2010，27(8):2991-2994.

［2］李菲，李天石，沈虹.再制造产品质量评价指标的重要度计算方法研究［J］.机床与液压，2009，37(6):38-41.LI Fei，LI Tian-shi，SHEN Hong.Study of importance calculation Method ofquality evaluation indexes for remanufacturing［J］.Machine Tool ＆ Hydraulics，2009，37(6):38-41.

［3］李延来，韩毅，姚建明，等.基于效用评价的质量功能配置中工程特性改进重要度确定的综合方法［J］.计算机集成制造系统，2009，15(3):585-591.LI Yan-lai，HAN Yi，YAO Jian-ming，et al.Integrated methodology for determining the improvement importance ratings of engineering characteristics in quality function deployment based on value evaluations［J］.Computer Integrated Manufacturing Systems，2009，15(3):585-591.

［4］许永平，石福丽，杨峰，等.基于QFD与作战仿真的舰艇装备需求分析方法［J］.系统工程理论与实践，2010，30(1):167-172.XU Yong-ping，SHI Fu-li，YANG Feng，et al.Requirement analysis method in naval battleships design based on QFD and operationalsimulation techniques［J］.Systems Engineering Theory ＆ Practice，2010，30(1):167-172.

［5］张居凤，汪玉，高兴华，等.武器装备论证需求分析方法研究［J］.哈尔滨工程大学学报，2011，32(1):119-123.ZHANG Ju-feng，WANG Yu，GAO Xing-hua.Method on requirements analysis of weapons and equipment demonstration［J］.Journal of Harbin Engineering University，2011，32(1):119-123.

［6］胡启洲，陆化普，蔚欣欣，等.基于关联熵与复合物元的公交系统综合测度模型［J］.系统工程理论与实践，2011，31(1):187-192.HU Qi-zhou，LU Hua-pu，YU Xin-xin，et al.Compressive measurement of urban public traffic system based on relational entropy and complex matter element［J］.Systems Engineering Theory ＆ Practice，2011，31(1):187-192.

［7］杜彦斌，曹华军，刘飞，等.基于熵权与层次分析法的机床再制造方案综合评价［J］.计算机集成制造系统，2011，17(1):84-88.DU Yan-bin，CAO Hua-jun，LIU Fei，et al.Evaluation of machine tool remanufacturing scheme based on entropy weight and AHP［J］.Computer Integrated Manufacturing Systems，2011，17(1):84-88.

［8］张维英，林焰，纪卓尚.多目标多层次船型方案模糊优选法［J］.中国造船，2004，45(3):31-37.ZHANG Wei-ying，LIN Yan，JI Zhuo-shang.Model for multi-objects and multi-layers system for ship form fuzzy optimization［J］.Shipbuilding of China，2004，45(3):31-37.