一类广义非负循环矩阵的逆谱问题

徐伟孺，雷英杰，顾先明

（1.中北大学理学院，山西 太原030051；2.电子科技大学数学科学学院，四川 成都611731）

0 引言

循环矩阵是一种具有优良性质的特殊矩阵，广泛地应用于声学、电动力学、图像处理、数理统计、数论、数值分析、平稳时间序列、线性回归和自适应光学与图像复原等领域.在非负矩阵理论中研究循环矩阵具有更显著的意义，其逆特征问题一直是该领域中的研究热点，在力学振动系统设计、分子结构理论、线性多变量控制理论及数值分析等领域中经常出现.文献［1-2］中给出了基本右循环矩阵的逆谱问题有解的充要条件，在此基础上，本文中主要对一类广义非负循环矩阵的逆谱问题进行讨论，分析非负r-循环矩阵和非负中心对称循环矩阵的性质.首先给出非负r-循环矩阵逆谱问题有解的充要条件和构造性算法，并在此基础上进行推广，继而给出非负中心对称循环矩阵逆谱问题有解的充要条件和构造性算法.其证明过程就是算法的构造过程.

根据非负循环矩阵谱的性质，将所给复数组σ＝（λ0；λ1，…，λn-1）限制如下：

且虚部为正的复数排在虚部为负的共轭复数的前面.约定Σ≡｛σ＝（λ0；λ1，…，λn-1）｜σ满足复数组限制｝是满足上述限制次序和条件的复数组集合，λ＝（λ0；λ1，…，λn-1）T表示n维列谱向量，［x］表示不大于x的最大整数，AT，AH分别表示矩阵A的转置矩阵与共轭转置矩阵，Ⅰn为n阶单位矩阵，Z为全体整数的集合为虚数单位.

由该定义可知：矩阵NCr（a）由它的第一行n个元素和参数r确定.

定义2 在矩阵NC1（a）中，如果ak＝an-k，k＝1，2，…，n-1，就称这样的矩阵为非负中心对称循环矩阵，记为NSC（a），a＝（a0，a1，…，an-1）T.

该定理说明矩阵NSC（a）由它的第一行个元素确定.

1 主要结果及证明

定理1.1［3］存在一个可逆矩阵Q（r），使得矩阵NCr（a）相似于一个对角矩阵.即

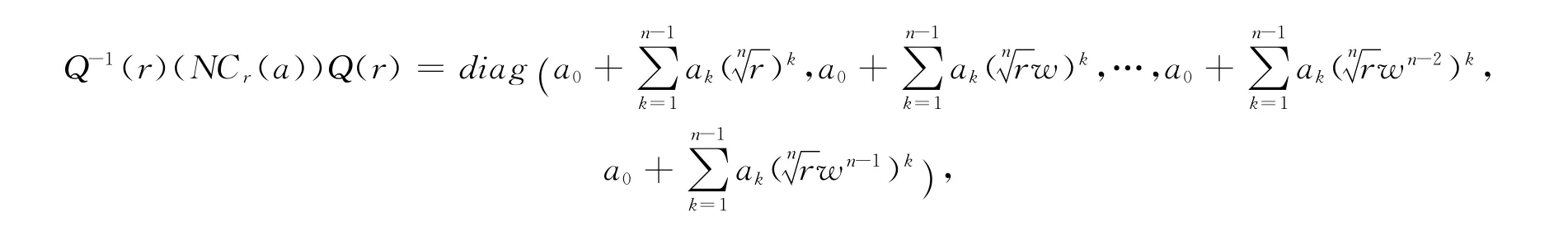
推论1.1［1-5］当r＝1时，NC1（a）酉相似于一个对角矩阵，其酉矩阵为Q（1）.

由定理1.1可以得到非负r-循环矩阵逆特征值问题的一个充要条件.

定理1.2 非负r-循环矩阵NCr（a）可实现谱σ＝（λ0；λ1，…，λn-1）∈Σ的充要条件是线性方程组

有唯一的非负解向量.

定理1.2的证明 必要性：若非负r-循环矩阵NCr（a）可实现谱σ＝（λ0；λ1，…，λn-1）∈Σ，则由定理1.1可知从而由可得线性方程组（1）式成立.又a＝（a0，a1，…，an-1）T≥0，可知线性方程组（1）式有非负解向量a.不妨设（1）式中的系数矩阵为V，则线性方程组（1）式变为Va＝λ.又矩阵V为Vandermonde矩阵，且第二列元素互异，故tr（V）＝n.又tr（V，λ）＝n.从而线性方程组（1）式有唯一解向量.故线性方程组（1）式有唯一的非负解向量.

充分性：已知σ＝（λ0；λ1，…，λn-1）∈Σ，若线性方程组（1）式有唯一的非负解向量a，则可由向量a中n个非负的分量构造一个唯一的非负r-循环矩阵NCr（a），使得矩阵NCr（a）实现谱σ＝（λ0；λ1，…，λn-1）∈Σ.证毕.

由谱分解理论可以构造非负r-循环矩阵，不妨设分别是矩阵的第j列的列向量.则可得如下定理：

定理1.3 非负r-循环矩阵NCr（a）可实现谱σ＝（λ0；λ1，…，λn-1）∈Σ的充要条件是为非负r-循环矩阵.

定理1.3的证明 必要性：若非负r-循环矩阵NCr（a）可实现谱σ＝（λ0；λ1，…，λn-1）∈Σ.由谱分解理论知NCr（a）的右特征向量为xj，左特征向量为yj，1≤j≤n.即

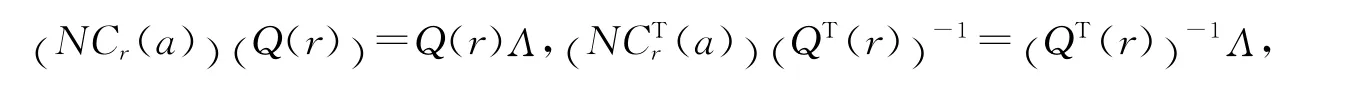
其中Λ＝diag（λ0，λ1，…，λn-1）.则有（y1，…，yn）Λ，又则

充分性：若已知谱σ＝（λ0；λ1，…，λn-1）∈Σ和非负r-循环 矩阵又由前提条件知（y1，…，yn）T（x1，…，xn）＝Ⅰn.不妨设则A＝ （x1，…，xn）Λ（y1，…，yn）T，在此等式两边同时右乘矩阵（x1，…，xn），则有A（x1，…，xn）＝（x1，…，xn）Λ.从而有Axj＝λj-1xj，1≤j≤n.即λ0，λ1，…，λn-1是矩阵的特征值.又是非负r-循环矩阵，从而可知可实现谱σ＝（λ0；λ1，…，λn-1）.证毕.

由定义2可知矩阵NSC（a）是矩阵NCr（a）的一个特例，从而可将矩阵NCr（a）的逆谱问题推广到矩阵NSC（a）的逆谱问题.首先给出如下定理：

定理1.4 存在一个正交矩阵Q，使得其中Λ＝diag（λ0，λ1，…，λn-1）.

从而可构造正交矩阵Q，使得QT＝Q-1.如下所示：当阶数n为奇数时

当阶数n为偶数时

由定理1.4知，如果一个非负中心对称循环矩阵实现谱σ＝（λ0；λ1，…，λn-1）∈Σ，则谱σ中相同的特征值成对出现且特征值全是实数.从而由定理1.2可得如下推论：

推论1.2 非负中心对称循环矩阵NSC（a）可实现谱σ＝（λ0；λ1，…，λn-1）∈Σ的充要条件是线性方程组

有非负解向量.

推论1.2的证明 必要性：若非负中心对称循环矩阵NSC（a）可实现谱σ＝（λ0；λ1，…，λn-1）∈Σ，则由定理1.4可知从而由可得线性方程组（2）式成立.又a＝ （a0，a1，…，an-1）T≥0，可知线性方程组（2）式 有非负解向量a.

充分性：若线性方程组（2）式有非负解向量.不妨设（2）式中的系数矩阵为C，则线性方程组（2）式变为Ca＝λ.由于λ∈Σ且λj＝λn-j，j＝1，…，n-1，则tr（C）＝tr（C，λ）＜n.从而可得到线性方程组（2）式的一个通解a＊，再由定义2可知分量aj≥0，通过对通解a＊的未知量赋值便可得解向量a＝（a0，a1，…，an-1）T，其中ak＝an-k，k＝1，2，…，n-1.从而可由向量a中n个非负的分量构造一个非负中心对称循环矩阵NSC（a）.证毕.

当n为奇数时，不妨设正交矩阵Q′的第j列的列向量为xj；当n为偶数时，设正交矩阵Q＊的第j列的列向量为yj.从而由定理1.3可得如下推论：

推论1.3 非负中心对称循环矩阵NSC（a）可实现谱σ＝（λ0；λ1，…，λn-1）∈Σ的充要条件是

（1）当n为奇数时是非负中心对称循环矩阵.

（2）当n为偶数时是非负中心对称循环矩阵.

2 实例分析

以下举出4个实例分别验证定理1.2～1.3、推论1.2～1.3中各个算法的有效性和实用性.根据文献［6］不难编制相应的MATLAB函数实现.

例1 已知σ＝（40.599 4；-5.458 4＋16.631 2i，-6.693 1＋6.114 0i，-4.296 4，-6.693 1-6.114 0i，-5.458 4-16.631 2i）和参数r＝2.由定理1.2编制 MATLAB函数后得到

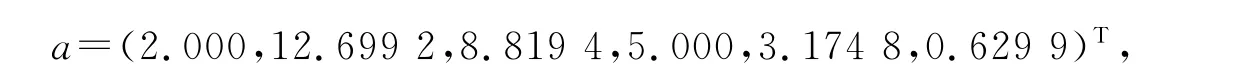
从而矩阵NC2（a）可实现复数组σ.

例2 已知σ＝（50.352 6；-11.380 7＋3.818 8i，12.528 7＋1.373 0i，5.175 7＋0.017 5i，5.175 7-0.017 5i，12.528 7-1.373 0i，-11.380 7-3.818 8i）和参数r＝3.运用定理1.3编制 MATLAB函数后得到a＝（9.000，3.653 8，4.751 3，7.616 9，6.327 4，2.155 3，0.701 7）T，

则矩阵NC3（a）可实现复数组σ.

例3 已知σ＝（23，8，-4，-7，-4，8），由推论1.2可编制 MATLAB 函数求出线性方程组（2）式的通解a＊＝（4，14，4，1，0，0）T＋k（0，0，1，0，-1，0）T＋l（0，1，0，0，0，-1）T.由定义2知14＋l＝-l，4＋k＝-k，即k＝-2，l＝-7.故a＝（4，7，2，1，2，7）T即为所求的非负解向量.从而矩阵NSC（a）可实现所给实数组σ.

［1］Chu M T，Golub G H.Inverse eigenvalue problems：theory，alogrithms and applications［M］.New York：Oxford University Press，2005.

［2］Rojo O，Rojo H.Some results on symmetric circulant matrices and on symmetric centrosymmetric matrices［J］.Linear Algebra And Its Application，2004，392：211-233.

［3］徐仲，张凯院，陆全.Toeplitz矩阵类的快速算法［M］.西安：西北工业大学出版社，1999.

［4］Gray R M.Toeplitz and circulant matrices：a review［J］.Foundations and Trends in Communications and Information Theory，2006，2（3）：155-239.

［5］Davis P J.Circulant matrices［M］.New York：John Wiley ＆Sons Inc，1979.

［6］Moler C.Numerical computing with MATLAB［M］.Philadelphia：SIAM，2004.

［7］Soto R L，Rojo O.Applications of a Brauer theorem in the nonnegative inverse eigenvalue problem［J］.Linear Algebra And Its Application，2006，416：844-85.