基于复折射率的偏振模型及其应用
马利祥,李范鸣,牛继勇,丁 雷
(1.中国科学院上海技术物理研究所,上海200083;2.中国科学院红外探测与成像技术重点实验室,上海200083)
1 引言
自1824年,阿拉贡首次观察到发光物体辐射出的偏振光,人类对偏振光的认识已有近两百年的历史[1]。但偏振成像技术作为一种探测手段用于目标探测和目标识别,则是始于20世纪80年代[2]。近年来,偏振探测技术,尤其是红外偏振探测技术发展迅速,已经逐渐从实验研究走向工程应用[3]。
偏振现象产生的机理以及偏振特性影响因素的理论机制,作为偏振成像的基础,一直没有得到深入的研究 。因此,通过建立目标表面的偏振模型,深入分析偏振产生的机理以及偏振特性影响因素的作用机制,是十分必要的。
本文首先介绍了偏振的基本概念和偏振模型建立的理论基础;然后介绍了基于复折射率的空气-光滑介质表面偏振模型;并介绍了偏振模型在分析反射辐射和自发辐射偏振性中的应用,分析了反射辐射和自发辐射对目标偏振特性的影响。最后给出了结论。
2 偏振建模的理论基础
2.1 偏振的基本概念
光波是一种电磁波(TEM波),以横波形式在各向同性介质中传输。在光与介质相互作用的过程中,起作用的主要是电场矢量,因此电场矢量E也称光矢量。
光矢量的振动相对于光波传播方向的不对称性叫做光波的偏振性。通常,用偏振度来描述光波的偏振性。偏振的定义是偏振性存在与否的核心判据,偏振度可以直观地描述偏振光的偏振程度。
为方便偏振建模,采用反射率R和发射率ε来定义偏振度:

其中,Rp和Rs分别表示介质表面光矢量平行方向和垂直方向振动分量的反射率;εp和εs分别表示介质表面光矢量平行方向振动分量的发射率。
为方便描述自发辐射,文中统一用θ来表示反射辐射的入射角和反射角,以及自发辐射的出射角。θ为观测角,定义为到达红外偏振成像系统的辐射与介质表面法线之间的夹角。
在已知反射率R和发射率ε的情况下,可以利用公式(1)求出反射辐射和自发辐射单独作用时的偏振度,从而可以清晰地分析反射辐射和自发辐射的偏振性随观测角的变化情况,即反射辐射和自发辐射偏振性的方向性。
2.2 偏振建模的理论基础
空气-介质表面偏振模型建立的理论基础主要有三个:斯涅耳定律、菲涅耳公式和基尔霍夫定律。
红外辐射入射到光滑的介质表面,θ0为入射角,θ1为折射角;n0为入射介质的折射率,n1为折射介质的折射率。
斯涅耳定律:斯涅耳定律也称折射定律,可以表示为:

斯涅耳定律用于描述入射角、折射角与对应两种介质的折射率之间的关系。
菲涅尔公式:空气-介质表面入射辐射垂直方向和平行方向振动分量在观测角为θ时的反射率可以写为:

菲涅耳公式用于描述非吸收性介质表面入射辐射、反射辐射和折射辐射之间的能量关系。
基尔霍夫定律:在给定的温度下,任何材料的发射率在数值上等于该温度时的吸收率。也可表述为,好的吸收体也是好的辐射体。基尔霍夫定律用于说明热平衡的物体,吸收率与发射率之间的关系。
3 空气-光滑介质表面模型
3.1 模型中的公式推导
菲涅尔公式主要用于描述非吸收性光滑介质表面的能量关系,不能表征目标的自发辐射。而在红外波段,自发辐射是目标的重要辐射来源。另外,实际应用中的目标多是吸收性的。因此,在红外波段分析目标的偏振特性时,不能简单套用菲涅尔公式。
由于吸收性介质的折射率为复数,因此W.J.Parker提出了一种改进的方法[5],用复数运算,改写菲涅耳公式,并综合菲涅耳公式和基尔霍夫定律,得出了平行方向和垂直方向光矢量分量反射率和发射率的公式。
定义光滑目标介质表面的折射率为n=n'+k'i,此时垂直方向和平行方向振动分量的反射率仍然可以用公式(2)表示,但公式中采用复数运算。
垂直方向和平行方向振动分量的发射率公式为[6]:

其中:
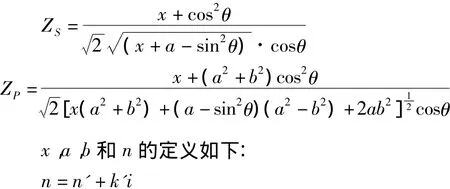

将公式(3)和(4)分别代入公式(1)中即可得到反射辐射和自发辐射单独作用时的偏振度。
3.2 空气-光滑介质表面模型
基于3.1节中介绍的公式进行建模,模型中做如下假设:
(1)空气-介质表面是单边界的;
(2)空气-介质表面是光滑的,不光滑的表面通过等效复折射率视为光滑表面;
(3)介质既可以是吸收性的也可以是非吸收性的,因此介质折射率是复数。
模型以观测角θ为输入,以复折射率n=n'+k'i为参数,输出为平行方向和垂直方向振动分量的反射率和发射率,以及反射辐射和自发辐射单独作用时的偏振度。
建模时,我们认为不同的目标材料具有不同的复折射率,不同粗糙度和不同程度的表面氧化物影响介质表面的吸收系数,即复折射率中的虚部。模型中,不考虑虚部的正负。例如,理想的铝板是光滑的,表面无氧化的,其复折射率为 n=4.45-31.5i[7]。实际的铝板表面有一定粗糙,且表面有氧化物,其复折射率近似为n=4.45-3.3i。因此,我们可以认为,介质表面的粗糙度和氧化物通过复折射率起作用。
介质表面的粗糙度和表面氧化物不会改变介质表面的折射性质,但会改变介质表面的偏振性质。
4 偏振模型的应用举例
红外偏振成像系统从红外场景中获取的红外辐射包含反射辐射和自发辐射。不同的波段,反射辐射和自发辐射所占的比重是不同的。因此分析反射辐射和自发辐射是否具有偏振性,以及分析反射辐射和自发辐射的偏振性对目标辐射的偏振性如何起作用具有重要的指导意义。
基于复折射率的空气-介质表面偏振模型,在求解反射率和发射率时,对平行分量和垂直分量进行了分解,因此依据2.1节介绍的偏振概念,我们可以对反射辐射和自发辐射的偏振特性进行验证和分析。选取理想的铝板作为仿真目标,其复折射率为n=4.45 -31.5i。
4.1 反射辐射的偏振性讨论
将铝板的复折射率n代入公式(3),得到垂直方向和平行方向光矢量振动分量的反射率。再将反射率代入偏振度的定义式(1),得到反射辐射单独作用时的偏振度。
对垂直方向和平行方向光矢量振动分量的反射率在Matlab中仿真,如图1所示。

图1 平行方向和垂直方向振动分量的反射率Fig.1 Reflectivity of parallel and perpendicular components
对反射辐射的偏振度在Matlab中进行仿真得到图2。

图2 反射辐射的偏振度曲线Fig.2 Curve of degree of polarization of reflective radiation
从图1中可以看出,在观测角为0°和90°时,平行方向振动分量的反射率与垂直方向振动分量的反射率是相等的,根据偏振的定义知道,此时反射辐射的偏振度为0,对比图2,也可以得出该结论。
在观测角度不为0°和90°时,即红外辐射倾斜入射时,垂直方向振动分量的反射率大于平行方向振动分量的反射率。也就是说,如果入射光是非偏振光,经过反射之后,反射辐射中垂直方向的振动分量会大于平行方向的振动分量。由偏振的定义可以知道,反射辐射是偏振的,从图2中也可以得到这样的结论。此时,我们定义该种偏振为正偏振性。
从图2中还可以看出,当观测角为87°时,反射辐射的偏振度达到最大,此时的观测角为布儒斯特角。非吸收的介质材料,偏振度最大为100%。复折射率对应吸收性材料,由于吸收性的存在,偏振度达不到100%。
4.2 自发辐射的偏振性讨论
菲涅尔公式仅适合描述反射辐射和折射辐射,不能描述目标的自发辐射。本文模型通过综合菲涅尔公式和基尔霍夫定律得到的公式,可以用来描述自发辐射。
将铝板的复折射率n代入公式(4),得到垂直方向和平行方向光矢量振动分量的反射率。再将反射率代入偏振度的定义式(1),得到反射辐射单独作用时的偏振度。
对垂直方向和平行方向光矢量振动分量的发射率在Matlab中仿真,如图3所示。

图3 平行方向和垂直方向振动分量的发射率Fig.3 Emissivity of parallel and perpendicular components
对自发辐射的偏振度在Matlab中进行仿真得到图4。
从图3中可以看出,在观测角为0°和90°时,平行方向振动分量的发射率与垂直方向振动分量的发射率是相等的,根据偏振的定义知道,此时自发辐射的偏振度为0,对比图4,也可以得出该结论。
当自发辐射倾斜出射时,平行方向振动分量的发射率大于垂直方向振动分量的发射率。也就是说,自发辐射中垂直方向的振动分量大于平行方向的振动分量。由偏振的定义可以知道,自发辐射是偏振的,从图4中也可以得到这样的结论。此时,我们定义该种偏振为负偏振性。

图4 自发辐射的偏振度曲线Fig.4 Curve of degree of polarization of emissive radiation
综合4.1和4.2,可以得出结论,对于空气-光滑的介质表面,反射辐射和自发辐射都是偏振的。反射辐射的偏振性为正偏振性,自发辐射的偏振性为负偏振性。自发辐射和反射辐射的偏振性是相互消减的。中波红外波段反射辐射和自发辐射所占比重相当,长波红外波段自发辐射所占的比重大于反射辐射,由于反射辐射和自发辐射偏振性的消减作用,使得长波红外波段的偏振成像效果优于中波红外波段。
5 结论
本文从物理建模的角度,依据斯涅耳定律、菲涅尔公式和基尔霍夫定律,针对空气-光滑介质表面,建立了一个用于分析红外辐射偏振性的模型。模型的应用方面,文中深入分析了反射辐射和自发辐射偏振性产生的机理,解释了同一目标在不同波段偏振性差异的来源。研究表明,本文建立的物理模型对研究红外偏振产生的机理,解释实际应用中的偏振现象,以及分析目标材料、目标表面粗糙度等对目标偏振特性的影响均有一定的作用。该模型的重要优势是可以简化复杂的影响因素,将其等效到复折射率中进行分析。下一步我们将利用模型,结合实验平台采集的偏振图像,深入研究粗糙度等因素对目标偏振特性影响的作用机制,为红外偏振成像技术的推广应用提供理论支持。
[1] Michael Bass,C M DeCusatis,J M Enoch,et al.Handbook of Optics[M].3rd.ed.USA:OSA,2010.
[2] Zhang Chaoyang,Cheng Haifeng,Chen Zhaohui,et al.The present research and developing trend of polarization remote sensing[J].Laser & Infrared,2007,37(12):1237 -1240.(in Chinese)张朝阳,程海峰,陈朝辉,等.偏振遥感的研究现状及发展趋势[J].激光与红外,2007,37(12):1237 -1240.
[3] Liu Biliu,Shi Jiaming,Zhao Dapeng,et al.Mechanism of infrared polarization detection[J].Infrared and Laser Engineering,2008,37(5):777 -781.(in Chinese)刘必鎏,时家明,赵大鹏,等.红外偏振探测的机理[J].红外与激光工程,2008,37(5):777 -781.
[4] Timothy J.Rogne,Frederich G.Smith.Passive target detection using polarized components of infrared signatures[J].SPIE,1990,117:242 -251.
[5] W J Parker,G L Abbott.Theoretical and experimental studies of the total emittance of metal[J].Symposium on Thermal Radiation of Solids,NASA SP -55,1964.
[6] B Ben-Dor.Polarization properties of targets and backgrounds in the infrared[C].SPIE,1992,1971:68 -77.
[7] M A Ordal,L L Long,R J Bell,et al.Optical properties of the metals Al,Co,Cu,Au,Fe,Pb,Ni,Pd,Pt,Ag,Ti,and W in the infrared and far infrared[J].Applied Optics,1983,22(7):1099 -1120.

