基于小波奇异值分析的汽轮机碰磨特征提取
胡三高, 安宏文, 马志勇, 柳亦兵, 滕 伟
(华北电力大学 能源动力与机械工程学院,北京 102206)
在机械设备故障诊断中,振动信号的突变部分往往包含丰富的故障信息,如零部件之间的变形、碰撞、摩擦和破损等.信号的突变程度常用奇异性来描述,因此突变检测可以归结为信号的奇异性检测问题.Mallat等[1]系统研究了小波变换与信号奇异性的关系,提出了基于小波变换的信号奇异值检测方法,该方法已广泛应用于各种机械设备的故障诊断中[2-4].
动、静部件之间的碰磨是旋转机械的常见故障.随着火电机组的大型化,碰磨故障造成的危害日益受到重视.对碰磨的转子动力学理论及检测技术的研究一直非常活跃.轴振监测是汽轮发电机组监测与保护的主要手段,通过对轴振信号的分析,可以有效诊断转子的不平衡、不对中以及油膜震荡等多种典型故障.碰磨故障是一类特殊故障类型,陆颂元等[5]总结了实际汽轮机轴系碰磨振动信号的特征,张善鹏等[6]分析了汽轮发电机组的一个实际碰磨案例.碰磨过程产生的结构振动响应具有瞬时冲击特性,每次发生碰磨的时间、部位和强度不确定,因而振动响应也存在差异.当发生轻微碰磨时,轴系冲击振动可能非常微弱,在噪声环境中难于识别,给故障特征的提取增加了难度,因此,各种现代信号分析技术被应用于分析和提取振动信号中的碰磨故障信息,如采用小波时频等高图方法[7]、局部波时频分布方法[8]、小波时频分析方法[9]以及二代小波[10]等.李曙光等[11]采用小波去噪与奇异性检测相结合的方法对短暂碰磨故障的发生区间进行了分析,Peng等[12]对不平衡、不对中、油膜震荡和碰磨故障振动信号的奇异性进行了系统地对比与分析.
笔者针对汽轮机碰磨故障所产生的轴系振动中的微弱冲击成分,首先通过小波变换对测量信号进行滤波处理,在特定尺度上提取碰磨产生的瞬时冲击成分,然后对该成分进行希尔伯特解调分析,用瞬时冲击信号的幅值包络反映信号在碰磨故障作用下产生的突变.对幅值包络信号进行连续小波变换,通过小波模极大值分析和李普西兹指数计算,确定碰磨故障引起的信号突变点位置.
1 小波变换与信号奇异性
1.1 信号奇异性与李普西兹指数
信号中常见的突变有2种:一种是边缘突变,相当于在该处叠加一个阶跃信号,对应信号转折点;另一种是峰值突变,相当于在该处叠加一个脉冲信号,对应信号峰值点.这2种突变点统称信号的奇异点.
数学上用李普西兹指数描述信号的奇异性.如果信号x(t)在t0附近存在n阶多项式Pn(t)和常数A,使得满足
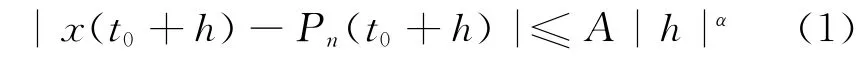
则称x(t)在t0具有李普西兹指数α.如果x(t)在t0处n次可微,但n阶导数不连续,则是n+1次不可微,其李普西兹指数n≤α<n+1.如果x(t)在t0处的李普西兹指数为α,则∫x(t)dt的李普西兹指数为α+1.如果信号在t0处不可微,其李普西兹指数必然小于1,则信号在该点是奇异的.
1.2 小波变换与信号奇异性的关系
信号x(t)的小波变换可以表示成信号与小波函数Ψ(t)的卷积形式
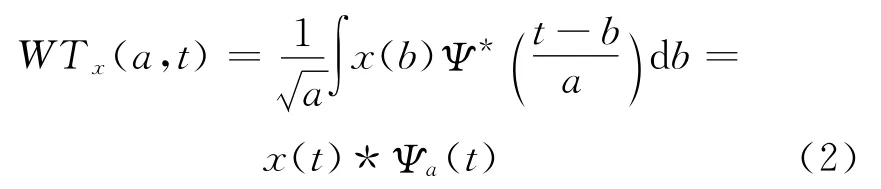
由式(2)可知,小波变换可以视为信号x(t)经过脉冲响应函数为Ψa(t)的系统的输出.如果Ψa(t)取为低通函数,满足

则信号通过该低通滤波器的输出仍然保留了信号x(t)中的奇异点信息,可以证明,对系统的输出求导数等价于以系统脉冲响应函数的导数对输入信号进行卷积.因此,如果取某个低通函数的导数作为小波函数Ψa(t),则得到的小波变换系数就可以反映信号x(t)中的奇异点信息.
1.3 小波变换模极大值与李普西兹指数
如果信号x(t)在t0处具有李普西兹指数α,则在t0附近存在如下关系
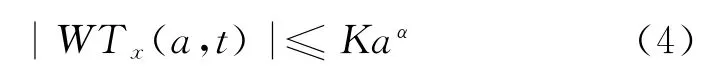
式中:|WTx(a,t)|为小波变换的模;K 为与小波函数有关的常数.
式(4)建立了小波变换与李普西兹指数的关系,对其两边取对数得
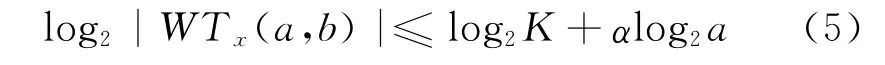
对于二进小波,a=2j,上式变为
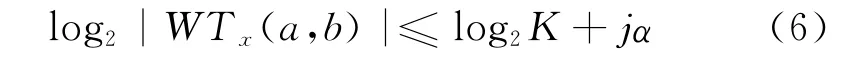
对于x(t)在t0处存在奇异点的情况,当t处在t0的左右邻域时,都满足
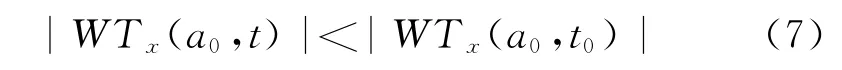
则(a0,t0)称为|WTx(a,b)|的模极大值点,对应的值|WTx(a0,t0)|称为模极大值,其在尺度 -时间(a-t)平面上的连线称为模极大值线.
显然,由式(5)可以得出以下结论:(1)如果信号x(t)在t0处的李普西兹指数α>0,则模极大值随尺度a的增大而增大;(2)如果信号x(t)在t0处的李普西兹指数α<0,则模极大值随尺度a的增大而减小;(3)如果信号x(t)在t0处的李普西兹指数α=0,则模极大值不随尺度a变化.
小波分析理论中给出的以下定理可以反映小波变换模极大值与李普西兹指数及信号奇异性的关系.

该定理指出,如果小波变换的模在一个区间内的小尺度方向上没有局部模极大值,则信号x(t)在该区间不存在奇异点.如果模极大值线在小尺度下收敛于t0,则t0是信号x(t)的一个奇异点.
2 汽轮机微弱碰磨信号奇异值检测
2.1 汽轮机碰磨信号
以某核电机组实际振动监测信号为例进行分析.图1为该汽轮发电机组的轴系结构及振动测点示意图.该机组在图中所示的各个轴承部位安装振动传感器,以监测绝对瓦振和相对轴振.

图1 机组轴系结构及振动测点示意图Fig.1 Structural diagram of the shaft system and arrangement of vibration measurement points
图2为某次停机降负荷过程中监测到的一段碰磨振动信号,分别为3号瓦振(3W)和轴振(3X)信号波形,信号采样频率为2500Hz.由图2可以看出,碰磨引起的瓦振冲击响应非常明显,呈现典型的衰减振荡特性,而轴振信号中碰磨引起的瞬变成分则很微弱.碰磨冲击响应在固体结构(缸体、轴承座等)上直接传播,因而监测到的响应信号往往比较明显,而轴系由于油膜支撑轴承的作用,对碰磨冲击振动的响应相对较弱.
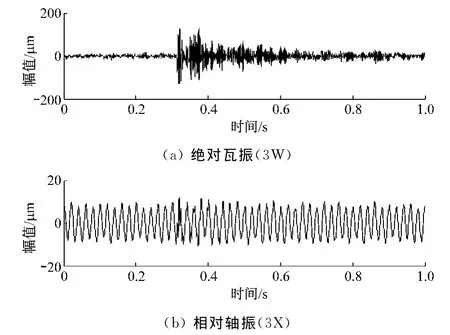
图2 碰磨过程的振动信号Fig.2 Vibration signals measured during rubbing fault
由于轴振监测是汽轮发电机组监测与保护的主要手段,以下主要针对图2中的相对轴振信号(3X)进行分析.图3为相对轴振信号(3X)的连续小波变换.由图3可知,在整个尺度系数范围内,小波变换的模极大值呈周期性变化,在各个尺度上都看不出反映碰磨故障的奇异性信息.因此,仅凭轴振时域信号的小波奇异值检测很难识别碰磨故障.
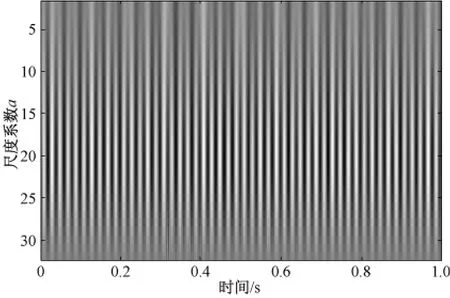
图3 碰磨过程中相对轴振信号(3X)的连续小波变换Fig.3 CWT of relative shaft vibration signal caused by rubbing fault(3X)
2.2 小波变换提取碰磨冲击成分
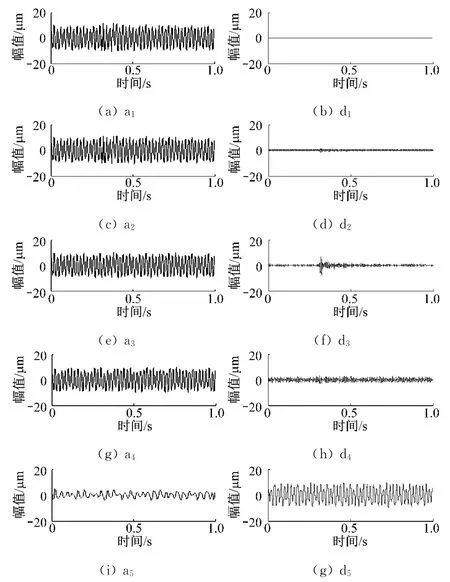
图4 碰磨过程中相对轴振信号(3X)的小波分解Fig.4 DWT of relative shaft vibration signal caused by rubbing fault(3X)
图4给出了采用db5小波对轴振信号(3X)进行5层分解得到的各层概貌(左列,a1~a5)和细节(右列,d1~d5)信号.可以看出,在第三层细节(d3)信号中,碰磨引起的冲击成分被清楚地显现出来.
为了突出碰磨引起的信号奇异性,采用Hilbert解调方法,对d3细节信号进行幅值包络分析,图5给出了d3细节信号及其幅值包络.通过包络分析,将小波细节信号中的碰磨冲击成分转换成幅值包络信号中的幅值突变成分,这样更有利于通过奇异值检测对碰磨发生的时刻进行自动精确识别与诊断.
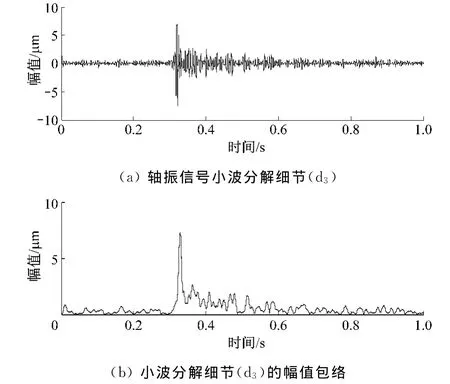
图5 小波分解细节d3及其幅值包络Fig.5 Amplitude envelop of wavelet detail d3
2.3 小波变换模极大值及李普西兹指数
针对包络信号中碰磨奇异点的冲击特征,采用奇对称的高斯小波(k=1)对包络信号进行连续小波变换,求出尺度系数在2~35范围的各个小波变换系数,连续小波变换计算结果如图6所示.对比图6和图3可以看出,经过小波滤波和包络解调后,小波奇异值检测明显提高.原始轴振信号中反映转频变化的周期性模极大值成分全部消失,只在碰磨发生时刻出现一个非常突出的模极大值线,可以清楚地识别碰磨故障引起的轴振信号的奇异性突变.

图6 幅值包络的连续小波变换Fig.6 CWT of the amplitude envelop
从幅值包络的小波变换中提取出模极大值,图7(a)为小波模极大值与小波尺度系数的关系曲线.根据式(5)可以计算出模极大值对应的李普西兹指数(见图7(b)).2个图中同时示出原始信号和包络信号在相同时刻的模极大值和李普西兹指数计算结果.由图7可以看出,原始信号在发生碰磨时刻的李普西兹指数随小波尺度系数的变化范围很大,小尺度系数对应的李普西兹指数远远大于1,没有反映信号奇异性的任何信息.而包络信号的李普西兹指数随尺度系数的增大而略有减小,取值范围在-1~1之间,可以清楚表明其模极大值对应的时间点为奇异点,信号在该时刻发生了突变.

图7 小波模极大值及其李普西兹指数Fig.7 Wavelet modulus maximal and corresponding Lipschitz exponents
3 结 论
当汽轮发电机组发生轻微动静部件碰磨故障时,产生的轴系振动信号突变成分非常微弱,直接采用小波奇异值检测方法很难发现故障.对包含故障信息的振动信号进行预处理,用小波多分辨率分析获取在特定尺度上的碰磨瞬时冲击信号,提取该瞬时冲击信号的幅值包络,可以清楚反映信号在碰磨故障作用下产生的突变信息.在此基础上,采用小波奇异值检测方法对碰磨引起的突变信息进行检测,可以明显改善微弱碰磨故障特征的提取效果.
[1]MALLAT S,HWANG W L.Singularity detection and processing with wavelets[J].IEEE Transactions on Information Theory,1992,38(2):617-643.
[2]刘献栋,杨绍普,申永军,等.基于奇异值分解的突变信息检测新方法及其应用[J].机械工程学报,2002,38(6):102-105.LIU Xiandong,YANG Shaopu,SHEN Yongjun,et al.New method of detecting abrupt information based on singularity value decomposition and its application[J].Chinese Journal of Mechanical Engineering,2002,38(6):102-105.
[3]ZHENG H,LI Z,CHEN X.Gear fault diagnosis based on continuous wavelet transform[J].Mechanical Systems and Signal Processing,2002,16(2/3):447-457.
[4]LOUTRIDIS S,TROCHIDIS A.Classification of gear faults using Hoelder exponents[J].Mechanical Systems and Signal Processing,2004,18(5):1009-1030.
[5]陆颂元,童小忠.汽轮机组现场动静碰磨故障的振动特征及分析诊断方法[J].动力工程,2002,22(6):2020-2024.LU Songyuan,TONG Xiaozhong.Vibration characteristics,analysis and diagnosis for rubbing between shaft/rotor and starts of turbine-generator in the field[J].Journal of Power Engineering,2002,22(6):2020-2024.
[6]张善鹏,周广顺.汽轮发电机组转子碰摩振动的理论分析及实例[J].动力工程,2003,23(6):2850-2854.ZHANG Shanpeng,ZHOU Guangshun.Theoretical analysis of steam turbo-generator rub vibration and examples[J].Journal of Power Engineering,2003,23(6):2850-2854.
[7]蒋东翔,刁锦辉,赵钢,等.基于时频等高图的汽轮发电机组振动故障诊断方法研究[J].中国电机工程学报,2005,25(6):146-151.JIANG Dongxiang,DIAO Jinhui,ZHAO Gang,et al.Study on methods of vibration fault diagnosisbased on time-frequency contour map for turbine generator unit[J].Proceedings of the CSEE,2005,25(6):146-151.
[8]胡爱军,安连锁,唐贵基.转子碰摩故障振动时频特征的实验研究[J].动力工程,2007,27(4):482-486.HU Aijun,AN Liansuo,TANG Guiji.Experimental study on time-frequency characteristics of rubbing initiated vibration of rotor[J].Journal of Power Engineering,2007,27(4):482-486.
[9]彭志科,何永勇,卢青,等.用小波时频分析方法研究发电机碰摩故障特征[J].中国电机工程学报,2003,23(5):75-79.PENG Zhike,HE Yongyong,LU Qing,et al.Using wavelet method to analyze fault features of rub rotor in generator[J].Proceedings of the CSEE,2003,23(5):75-79.
[10]姜洪开,王仲生,何正嘉.基于改进第2代小波算法的发电机组碰摩故障特征提取[J].中国电机工程学报,2008,28(8):127-131.JIANG Hongkai,WANG Zhongsheng,HE Zhengjia.Impact-rub fault feature extraction for generation unit using improved second generation wavelet algorithm[J].Proceedings of the CSEE,2008,28(8):127-131.
[11]李曙光,张梅军.小波去噪与奇异性检测相结合诊断动静件短暂碰磨故障发生区间[J].机械设计,2010,27(10):79-81.LI Shuguang,ZHANG Meijun.Diagnosis of transient impact and friction fault interval of dynamic and static parts by integration of wavelet denoising and singularity detection[J].Journal of Machine Design,2010,27(10):79-81.
[12]PENG Z K,CHU F L,PETER W,et al.Singularity analysis of the vibration signals by means of wavelet modulus maximal method[J].Mechanical Systems and Signal Processing,2007,21(2):780-794.

