基于ANSYS／LS－DYNA的带冠叶片碰撞振动特性的有限元分析

陈镇南， 卢绪祥， 李录平， 黄章俊， 晋风华

（长沙理工大学 能源与动力工程学院，长沙 410114）

叶片是大型透平机械实现能量转换的关键部件之一.在汽轮机运行中，叶片不断承受着交变汽流力的作用而产生受迫振动，从而导致叶片振动疲劳损坏.国内数据统计，叶片损坏事故约占汽轮机事故的40%，其中60%～80%的损坏是叶片振动疲劳损坏.采用自带冠叶片减振是目前涡轮叶片常用的控制叶片振动的方法.自带冠叶片已广泛应用于电站汽轮机、电站燃气轮机及航空涡轮机上.运行实践表明，这种叶片可以降低叶片振动应力，可靠性高，而且便于设计顺畅的通流部分以提高效率［1］.

在工程机械中，碰撞是迅速传递和消耗能量的有效方法之一.冠间接触碰撞减振结构通过碰撞的限位作用大大减小了叶片振动的幅值，同时叶片间相互接触碰撞耗散振动能量，减小激振力能量的输入，起到减振作用［2］.带冠叶片的冠间接触碰撞相当复杂，在碰撞和滑移的联合作用下，叶冠之间的接触面会处于黏着、滑动和脱离等状态.整个接触碰撞的过程伴随着摩擦引起的接触力的变化，接触面上各点的运动状态并不一致.因此其接触碰撞过程相当复杂，具有典型的非线性特征［3］，理论研究难度较大.目前许多学者采用接触有限元法对其动力学问题进行求解，运用大型通用有限元软件如 MSC／Nastran、Ansys、Abaqus等来分析系统的碰撞振动特性［4-7］.

Ansys／LS－DYNA是用于求解高度非线性问题的通用显式动力学有限元分析程序，它能有效处理多种接触碰撞及大变形问题.笔者以锯齿形带冠叶片组为研究对象，采用Ansys／LS－DYNA进行非线性碰撞仿真分析，研究了碰撞阻尼减振效果与振动系统各参数之间的关系，模型充分考虑了叶冠之间存在间隙时叶片受到激振力后冠间的撞击和摩擦对叶片振动能量的吸收与耗散，并且对具体叶片模型接触碰撞系统的响应特性及减振机理进行了分析.

1 冠间接触碰撞有限元计算模型

1.1 叶冠动力学模型

在叶片顶部，相邻叶冠间在安装时留有一定的初始间隙，工作时由于气流力等外力作用，叶片发生振动，当两个叶片的相对位移大于装配间隙时，叶片之间发生接触碰撞和摩擦［8-10］.叶冠间的碰撞限位、接触面间的摩擦同时耗散叶片的振动能量，起到减振作用.摩擦因数依赖于接触面的相对滑动速度，一般情况下，静摩擦因数高于动摩擦因数.笔者采用指数衰减摩擦模型来描述叶冠之间的摩擦［11］.

式中：μ为摩擦因数；μD为动摩擦因数；fa为静摩擦因数与动摩擦因数之比；dc为衰减系数；vr为摩擦面之间的滑动速度.

式中：k为接触面刚度（接触面刚度由单元尺寸和材料特性确定），N／mm；δ为穿透深度，mm.

1.2 带冠叶片显式动力学计算模型

自带冠叶片接触碰撞动力学有限元方程为

式中：M、C、K分别为质量矩阵、阻尼矩阵和刚度矩阵；U、、分别为位移向量、速度向量和加速度向量；F为叶冠之间相互碰撞的非线性力与气流激振力，N.

采用显式中心差分法（显式直接积分法）求解方程（3），即：

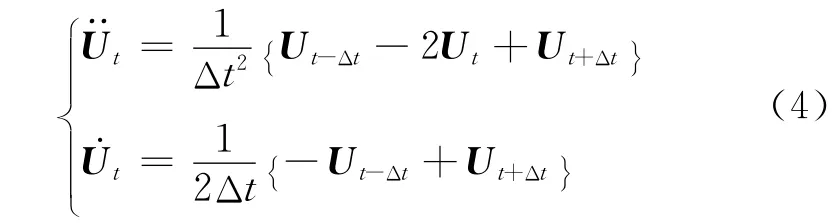
将式（4）代入式（3）进行迭代求解，经整理可得：

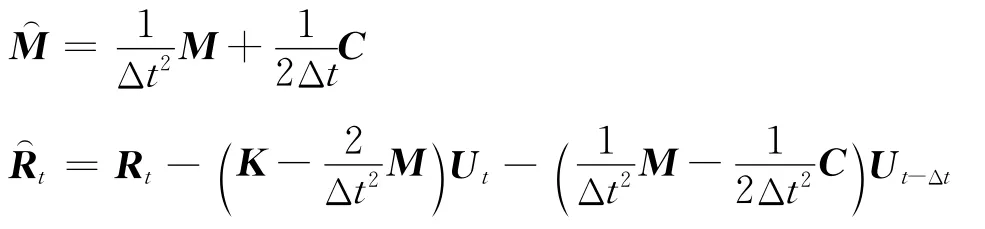
通过t＋Δt时刻的瞬时位移向量Ut＋Δt可以获得t＋Δt时刻的单元应力与单元应变.

我小学同学的母亲、有一半东欧血统且在苏联多年的亚兰阿姨，在1982年左右曾专门跟我说过“三种树比拟三种人”，印象深刻，令人叫绝，但我却一直没有替她写出来，欠疚至今。

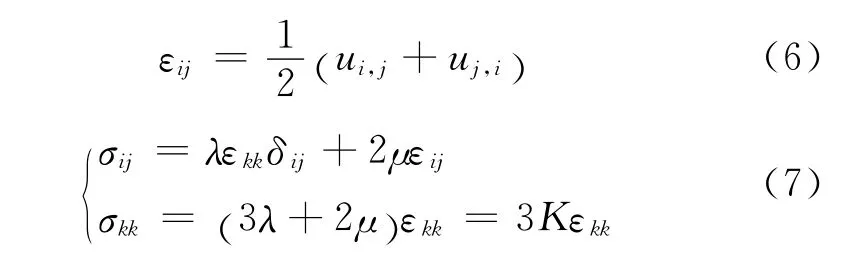
式（6）表明应变分量εij满足二阶张量的坐标变换关系；式（7）表明任意坐标系下各向同性体应力分量与应变分量的关系；λ、μ均为拉梅弹性常数.

利用中心差分数值方法求解方程可以获得足够精确的近似值，为求解动力系统响应提供了有力的计算工具.然而，中心差分格式还存在一个能否收敛的问题，该积分方法要求时间步长Δt小于一个临界值Δtcr，即可满足迭代收敛要求，即

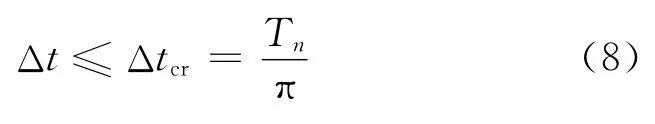
式中：Δtcr由整个单元集合体的刚度和质量的性质算出，s；Tn是系统固有振动中的最小周期，s；n是该系统的维数.

如果使用一个大于Δtcr的时间步长，则积分是不稳定的，这意味着由数值积分的舍入所导致的误差都会增大，并且在许多情形下会使响应计算失去意义.

2 有限元模化及边界条件

以试验用带锯齿型冠矩形平板直叶片为研究对象，该叶片结构简单，能反映出各影响因素单独作用时的效果，且为理论分析提供方便适用的有限元模型.叶片的结构参数为：叶片长500mm，宽50mm，厚5mm.采用Q235钢，材料弹性模量为2.05×1011N·m2，密度为7850kg／m3，泊松比为0.29.

2.1 单元类型的选择

在有限元分析中，梁单元和板壳单元模型可为叶片的分析提供一定的指导，但其忽略了叶片的某些结构因素，使得分析模型与真实叶片存在差距.而三维实体单元模型能较好地描述叶片的复杂结构，精确地反映叶片的应力应变情况.故采用Solid 164三维八节点实体单元来模化带冠叶片.

2.2 网格的划分

有限元网格的自动划分是建立有限元模型的重要技术，是将整体结构离散化，进行数值分析的前提.将叶片实体模型导入LS－DYNA软件，在GUI界面设置网格划分精度，进行智能网格划分.单元尺寸设置0.5，节点数为3768个，单元数为9807个.经模化后的带冠单叶片、三叶片组有限元模型见图1.

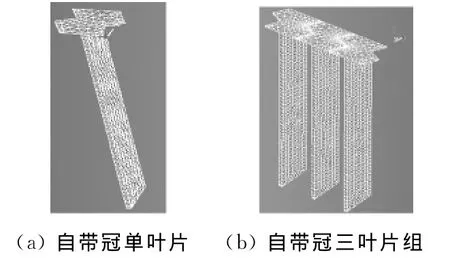
图1 带锯齿型冠叶片有限元模型Fig.1 Finite element model for blades with zigzag shroud

2.3 边界条件的确定

在有限元分析过程中，边界条件（或加载方式）的设置对分析精度有很大影响.通常的原则是在保证模型自由度得到准确约束的前提下，尽量不要人为添加模型原本不具备的限制条件.根据叶片在装配时的实际受力情况，对于带冠叶片组，在叶根与叶轮装配环紧固部分以及叶根与叶轮接触部分施加全约束.冠间相邻接触边界设置接触约束，LS－DYNA程序的罚函数法通过在节点与接触表面之间引入弹性弹簧来建立接触刚度，使冠间接触面满足接触面无穿透约束条件，同时在接触界面相对运动时考虑摩擦力的作用.具体的激励加载及边界条件设定见图2.

与隐式静力分析不同，所有显式动力分析施加的载荷必须是时间的函数，避免出现单点载荷，否则它们会激起沙漏模式.为模拟真实叶冠存在接触碰撞阻尼时的振动特性，分别对三只叶片同时施加简谐激振力，通过改变激振力的频率、幅值及相位使其发生接触碰撞，探讨碰撞阻尼减振效果与振动系统各参数之间的关系.在Ansys／LS－DYNA程序中对结构进行加载需要遵循以下步骤：（1）将模型中受载的部分定义成组件，对于刚体采用PART号；（2）定义各个时间间隔以及对应载荷值的数组参数；（3）将载荷施加到结构模型特定受载的部分上.

图2 带锯齿型冠叶片加载与约束示意图Fig.2 Schematic diagram for loading and constraint of blades with zigzag shroud

计算时对叶片组施加的简谐激振力如式（9）

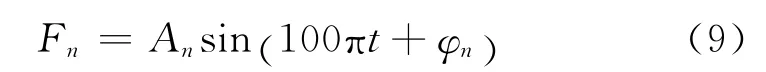
式中：An为激振力幅值，N；n＝1，2，3；t＝0，0.01s，0.02s，…，0.08s.

3 带冠成组叶片碰撞阻尼振动特性分析

3.1 冠间间隙对碰撞减振效果的影响

带冠叶片的碰撞减振结构设计中，冠间间隙是一个重要的结构参数，工程实际应用也证明了冠间间隙对带冠叶片碰撞振动响应有重要影响［3］.为更真实地模拟带冠叶片在运行时所受的激励状态，笔者对不同间隙模型下的三只叶片同时施加简谐激振力，研究其在不同间隙下的动力响应特性.对叶片组施加相同幅值和频率、相位差值为180°的简谐激振力，激振力大小为1N，频率为50Hz.相邻叶冠间的间隙分别为1mm、0.7mm、0.5mm、0.4mm、0.3 mm、0.2mm、0.1mm、0.05mm 和0（不施加预紧力，使接触面发生准接触）.取中间叶片叶冠76号节点作为考核点，其振动响应幅值曲线见图3.

图3为不同冠间间隙下带冠叶片发生碰撞振动时最大振幅的变化曲线.叶片动力响应的幅值越小，表明叶片振动时产生的动应力越小，此时接触碰撞的减振效果越好.结合叶冠间接触应力分布云图，通过分析发现当冠间间隙大于1mm后，叶冠接触面接触状态的转换比较复杂，碰撞、黏滞、滑移等现象共存，所以此时叶片顶部的响应值也较大.当间隙为0.1mm时，响应幅值比间隙为0.3mm时增大了58%，此时叶冠之间的接触状态主要为滑动摩擦.另外，并不是间隙越小减振效果越好，随着冠间间隙的减小，存在一个最合适的冠间间隙区间（由图3得出最优区间为0.25～0.35mm），使得碰撞减振效果达到最佳，这一点与文献［10］的结论一致.分析得知，在简谐激振力作用下，冠间间隙的改变可使振动的叶片接触相邻叶片时碰撞速度不同，从而引起碰撞能量的改变.同时，碰撞后叶片之间相互耦合进入滑动摩擦阶段，碰撞后速度的改变也会引起摩擦时消耗的能量不同，因而对减振效果有很大影响.

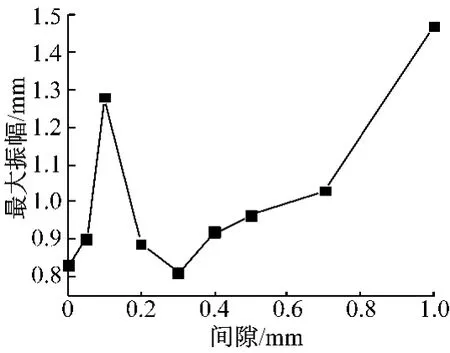
图3 冠间间隙大小与振动响应幅值的关系Fig.3 Relationship between tip gap and amplitude of vibration response

3.2 激振力相位差对碰撞减振效果的影响

激振力分析是叶片动力响应分析的前提.笔者利用初始间隙为0.1mm的带冠叶片组模型探讨激振力相位差对叶片组碰撞减振效果的影响.通过改变作用在叶片上的激振力相位差，得到中间叶冠上76号节点的振动响应如图4所示.

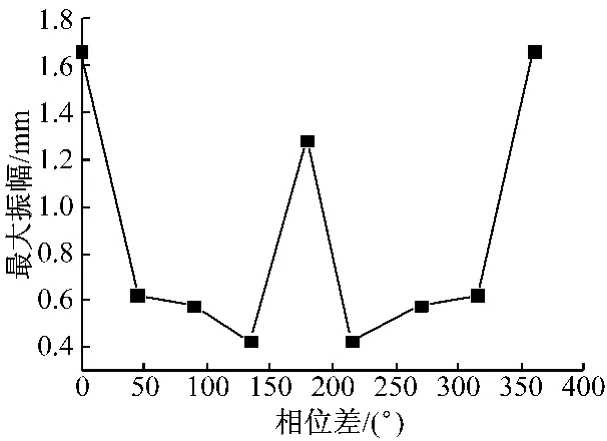
图4 激振力相位差与振动响应的关系Fig.4 Relationship between phase difference of exciting force and amplitude of vibration response

从图4可以看出，当施加在叶片组上的激振力相位值相同时（0°或360°），振动响应幅值最大.显然，激振力相位相同时，叶片同步振动，叶冠之间的碰撞阻尼并没有产生作用，其响应幅值与自由叶片一样；当激振力的相位差值逐渐增加时，叶片动力响应幅值不断减小，相位差在50°～150°时，响应幅值变化幅度较小，此时叶冠之间产生黏滞现象，并且叶冠接触部分发生变形，这种变形消耗了振动能量；当激振力相位差等于180°时，由于叶片阻尼围带之间存在激烈碰撞，叶冠接触部分变形较大，叶片顶部的最大振动响应值急剧上升，相位差为135°时，增幅达68.3%.

3.3 激振力幅值对碰撞减振效果的影响

激振力大小对叶片振动特性有很大影响.为研究激振力大小对带冠叶片组碰撞减振效果的影响，讨论了冠间间隙为0.1mm时的带冠叶片组在不同激振力幅值下的动力响应特性.分别施加幅值为1N、3N、5N、7N、9N、11N 和13N，频 率 为50 Hz的简谐激振力，整理不同激振力下考核点等效应力的最大值，分别取中间叶片叶冠1607号单元及叶根837号单元作为考核点，作出其振动应力响应曲线（图5）.

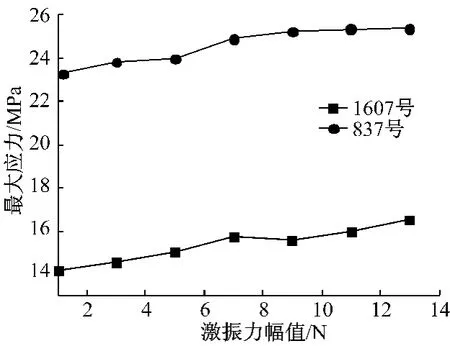
图5 激振力幅值与振动应力响应的关系Fig.5 Relationship between amplitude of exciting force and stress of vibration response

由图5可知，随着激振力幅值的增大，最大应力整体呈小幅上升趋势，但并非呈直线式增加，因为激振力的改变导致叶片碰撞速度变化，而碰撞过程中能量的消耗与振动速度变化不是线性关系，从而引起碰撞能量的消耗与激振力幅值也不是线性关系.另外，叶片应力峰值的整体变化量不大，表明碰撞的激烈程度对碰撞阻尼减振效果的影响不明显，即碰撞阻尼对激振力不敏感，这与文献［1］所得的结论一致.说明在叶片承受不同激振力时，采用碰撞减振结构的叶片组能够取得较好的减振效果，这是带碰撞阻尼结构叶片的一个优良特性.

4 结 论

（1）叶冠间隙对碰撞减振效果有很大影响，并呈现明显的规律性，初始间隙越小，碰撞减振效果越好；碰撞减振系统存在最优间隙范围，文中间隙为0.25～0.35mm时能取得很好的减振效果，间隙为0.3mm时，响应值降幅达45%.

（2）激振力大小的变化对带锯齿型冠叶片碰撞减振效果影响不大，这是碰撞阻尼的一个优良特性.

（3）激振力相位差改变时，叶片组碰撞减振效果具有明显的规律性，当激振力相位差为50°～150°时能取得较好的减振效果.

（4）利用 ANSYS／LS－DYNA 软件的动态显式算法可以较好地模拟带锯齿型冠叶片接触碰撞过程，分析模型及计算结果对于理解叶冠之间接触碰撞阻尼的减振机理具有一定的参考价值.

［1］徐大懋，李录平，须根发，等.自带冠叶片碰撞减振研究［J］.电力科学与技术学报，2007，22（1）：1－6.XU Damao，LI Luping，XU Genfa，et al.Research on impact damping of integrally shrouded blades ［J］.Journal of Electric Power Science and Technology，2007，22（1）：1－6.

［2］马晓峰，刘占生，张广辉，等.自带冠叶片冠间接触碰撞动力学建模及数值模拟［J］.汽轮机技术，2009，51（5）：361－366.MA Xiaofeng，LIU Zhansheng，ZHANG Guanghui，et al.Modeling and numerical simulation of contact collision dynamic between the tips of blades［J］.Turbine Technology，2009，51（5）：361－366.

［3］武新华，李卫军.自带冠叶片冠间接触碰撞减振研究

［J］.汽轮机技术，2005，47（1）：41－44.WU Xinhua，LI Weijun.Research on damping of contract or impact of blades'tips［J］.Turbine Technology，2009，47（1）：41－44.

［4］李剑钊，闻雪友，林志鸿.汽轮机带冠叶片振动特性研究进展［J］.汽轮机技术，2005，47（4）：241－243，247.LI Jianzhao，WEN Xueyou，LIN Zhihong.The advancement of study on vibration characteristics of shrouded blade of steam turbine［J］.Turbine Technology，2005，47（4）：241－243，247.

［5］王小宁，陈勇，杜朝辉，等.带锯齿冠叶片振动特性的数值模拟［J］.动力工程学报，2010，30（8）：589－593.WANG Xiaoning，CHEN Yong，DU Zhaohui，et al.Numerical simulation of the vibration characteristicsfor the blade with zigzag shroud［J］.Journal of Chinese Society of Power Engineering，2010，30（8）：589－593.

［6］WANG Y，CHEN X，GINDY N，et al.Elastic deformation of a fixture and turbine blades system based on finite element analysis［J］.Int J Adv Manuf Technol，2008，36（3／4）：296－304.

［7］李录平，晋风华，李杰，等.透平叶片几种减振结构的阻尼特性试验研究［J］.动力工程，2004，24（6）：793－797.LI Luping，JIN Fenghua，LI Jie，et al.Experimental research on damping characteristics for turbine blades［J］.Journal of Power Engineering，2004，24（6）：793－797.

［8］卢绪祥，黄树红，刘正强，等.基于谐波平衡法的带冠叶片接触碰撞减振特性研究［J］.动力工程学报，2010，30（8）：578－583.LU Xuxiang，HUANG Shuhong，LIU Zhengqiang，et al.Study on contact－impact damping characteristics of shrouded blades based on harmonic balance method［J］.Journal of Chinese Society of Power Engineering，2010，30（8）：578－583.

［9］刘占生，张敏，张广辉，等.基于LuGre摩擦模型的叶片碰撞摩擦特性研究［J］.振动与冲击，2012，31（12）：172－178.LIU Zhansheng，ZHANG Min，ZHANG Guanghui，et al.Characteristics of impact－contact and friction between tips of blades based on LuGre model［J］.Journal of Vibration and Shock，2012，31（12）：172－178.

［10］卢绪祥，刘正强，黄树红，等.含间隙碰撞振动系统的非线性振动特性［J］.动力工程学报，2012，32（5）：388－393.LU Xuxiang，LIU Zhengqiang，HUANG Shuhong，et al.Nonlinear vibration characteristics of a vibro－impact system with clearance［J］.Journal of Chinese Society of Power Engineering，2012，32（5）：388－393.

［11］O John.LS－DYNA Theoretical Manual［M］.Livermore Software Technology Corporation，California，1998.