悉尼自适应交通控制系统线圈数据短时多步预测双层模型

李 琦，姜桂艳

（1.吉林大学 交通学院，长春130022；2.青岛市城市规划设计研究院，山东 青岛 266011；3.宁波大学 海运学院，浙江 宁波 315211）

0 引 言

悉尼自适应交通控制系统（Sydney coordinated adaptive traffic system，SCATS）在世界范围内得到了广泛的应用。1986年上海在国内最早引入SCATS系统，随后天津、广州、沈阳、杭州、苏州、宜昌等许多城市也开始采用该系统控制城市交通［1－2］。目前，SCATS 线圈获取的动态交通数据（平均车头时距和交通流量）仅用于交通信号控制。从数据共享的角度看，如果能够将其所获得的动态交通数据应用于该系统所覆盖道路的交通拥挤预测，对于低成本改善交通控制、交通诱导和交通指挥的协调性具有重要的现实意义。

短时交通预测是智能交通系统（ITS）研究与应用的关键技术之一［3］。然而，目前国内外对于短时交通预测的研究大部分局限于一步预测［4－8］，这种预测结果实际上只能修正信息采集与处理的时间延迟，是对当前时段交通状态的估计，无法支持交通管理者和交通出行者进行预见性决策。尽管文献［9］提出了一种多步预测方法，但其采用的是固定预测步数，不能针对某个时间段内交通数据序列的特性决定其可预测步数，在一定程度上影响了多步预测的效果。

为了克服已有研究成果的缺陷，文献［10］针对城市快速路线圈获取的5min采样间隔的交通数据，提出了一种交通数据动态可预测性分析方法，可对交通数据序列的可预测程度进行在线分析。由于短时交通预测的数据基础是固定采样间隔下的交通数据时间序列，而SCATS以绿灯信号相位为采样时间单位获取交通数据，相位时长是动态变化的，因此在SCATS中各个采样间隔内的交通数据不具有严格的时间可比性，使得文献［10］中的方法不能直接用于SCATS线圈数据的多步预测。而且，该方法通过设计关联数据特征指标建立可预测步数估计模型，而关联数据特征指标的使用在一定程度上会导致交通参数时间序列特征信息的损失。此外，该方法采用移动平均这种线性方法对交通参数进行多步预测，难以体现交通数据序列中的非线性特征。因此，文献［10］的方法在可预测步数的确定以及多步预测效果方面还存在进一步提升的空间。

人工神经网络以其良好的非线性逼近能力在短时交通预测领域得到了广泛的应用，但目前相关文献采用的都是静态神经网络［7－10］，其输出只依赖于当前的输入，缺少反馈或时延成分。与静态神经网络相比，动态神经网络具有更强的动态系统逼近能力，在非线性动态系统中的应用效果更 好［11］。 NARX （Nonlinear autoregressive model with exogenous inputs）神经网络和FTD（Focused time－delay）神经网络是目前最为常用的两种动态神经网络，本文将以此为基础设计SCATS线圈数据的短时动态多步预测方法。

综上所述，本文在采用文献［12］提出的虚拟时间序列构建方法对SCATS线圈数据进行预处理的基础上，提出了以NARX神经网络为基础设计SCATS线圈数据的多步预测方法，和以FTD神经网络为基础设计SCATS线圈数据的可预测步数在线估计方法，并采用某特大城市SCATS线圈实测数据进行验证和对比分析。

1 基于NARX神经网络的SCATS线圈数据多步预测方法

1.1 多步预测问题的描述

时间序列预测是利用研究对象在当前或之前若干时间间隔的数据对其未来取值进行的估计。当需要进行多步预测时，通常可将已获得的预测值作为已知数据用于下一时间间隔的预测。

对于一步预测，其数学模型可表示为

利用相同的预测函数，两步预测模型可表示为

上述的迭代多步预测将预测值引入自变量，会产生误差传导，当预测的步数较多时，这种传导误差会比较严重，因此降低每一步的预测误差都是非常重要的。

1.2 多步预测模型的建立

NARX神经网络是一种动态递归网络，通过引入时延与反馈变量，将神经网络的函数模拟功能与时间序列的数据关联特性相结合，有助于改善动态非线性系统的估计效果。采用NARX神经网络进行多步预测能够在各步预测误差较小的情况下进行下一步预测，从而可削弱误差传导带来的负面影响。

NARX神经网络的输入由两部分构成:一部分是外部输入，另一部分是反馈输入。其模型可表示为

NARX神经网络的基本结构如图1所示。其中，反馈输入可以为研究对象的实测值，也可以为NARX网络获得的估计值，不过利用实测值作为反馈输入训练的NARX网络拟合效果更优。

图1 NARX神经网络的基本结构Fig.1 Architecture of NARX neural network

考虑到交通数据序列是随着时间的推移而不断演化的，可将其视为时间因素的函数，因此在利用NARX神经网络对SCATS线圈数据进行多步预测时，本文将各时间间隔对应的时间点序列视为，将交通参数（如平均车头时距或交通流量数据序列）视为Yt。在线应用时，用Y的预测值逐步替换其在输入变量中的实测值，即可实现迭代多步预测。

文献［11］证明了含有1个隐含层的NARX神经网络可以逼近任意非线性连续函数，因此将隐层数设置为1。激励函数选择sigmoid函数，训练算法采用Levenberg－Marquardt算法。选择目前最为常用的平均相对误差 MAPE［13］作为NARX神经网络性能的评价指标，其值越小，说明NARX神经网络的性能越优。

考虑到相同日期（周一，周二，…，周日）的交通模式具有较强的相似性［12］，对于每一检测器，在建立多步预测模型时，以相同日期的交通模式为基础。

2 基于FTD神经网络的SCATS线圈数据可预测步数在线估计方法

2.1 可预测步数在线估计的基本原理

在应用上一节提出的多步预测方法时，只要不停止运行，则可以对SCATS线圈数据进行无限多步的预测。但实证分析表明，在特定时间点上进行多步预测时，每一步的预测误差与预测步数之间存在正相关关系，满足期望误差的预测步数不可能无限多。为此文献［10］最先提出了交通数据序列的动态可预测性的概念，并针对城市快速路线圈的5min交通数据，设计了一种可预测步数在线估计方法。其基本原理是:①分析实际交通数据序列的动态特性，建立关联数据特征指标向量，并获得每个时点处的关联数据特征指标向量值；②在指定期望预测误差的情况下，运用一定的预测方法获得每个时点处可满足预测误差要求的预测步数；③运用BP神经网络建立关联数据特征指标向量与可预测步数之间的映射关系；④在实际运用过程中，根据所获得的动态交通数据，在线计算当前时点的关联数据特征指标向量值，并据此估计此时的可预测步数。

为了更充分地利用交通参数时间序列中所包含的可预测性信息，不再设计关联数据特征指标，而是直接将交通参数的时间序列本身（包括时间点序列和交通参数数据序列）作为输入变量，并基于FTD神经网络建立新的可预测步数估计模型。

2.2 可预测步数在线估计模型的建立

在交通数据序列和多步预测方法一定的条件下，交通参数可预测步数是指特定时点上交通数据序列多步预测结果的相对误差连续小于阈值z的最大步数。因此，交通参数可预测步数是一个非实测参数，无法应用前述的NARX神经网络建立估计模型。作为一种动态时延神经网络，FTD神经网络特别适用于研究对象的实测值无法在线获取的情况［14］，其基本结构如图2所示。图2中，输入变量数据序列为，输出变量数据序列为Bt。

图2 FTD神经网络的基本结构Fig.2 Architecture of FTD neural network

FTD神经网络通过在输入层引入时延变量，其输出结果不仅依赖于当前时间间隔的输入变量，还依赖于之前若干时间间隔的输入变量（），能够更为充分地利用已有的输入变量信息。

FTD神经网络的隐层数通常可设置为1，激励函数选择sigmoid函数，训练算法采用Levenberg－Marquardt算法。

可预测步数是离散变量且数值通常较小，使用平均相对误差MAPE不能直观地表达可预测步数的估计效果，例如当两组估计值和真值分别为2、1以及6、3时，尽管MAPE都为100%，但显然前者的估计效果更优。因此，为了能够直观表达可预测步数估计值与真值之间绝对差异的平均水平，选择平均绝对误差MAE［13］作为FTD神经网络的性能评价指标，该值越小说明FTD神经网络性能越优。

3 基于遗传算法的动态神经网络结构优化方法

时延长度和隐层神经元的个数决定了NARX和FTD神经网络的基本结构，不同的（d，N ）或者（d1，N1）对应不同的网络结构，因此应选用具有最佳性能的网络。遗传算法是一种基于生物自然选择与遗传机理的全局优化算法［15］，本文利用遗传算法优化两种动态神经网络的结构。

在进行编码操作时，本文采用目前遗传算法中最常用的二进制编码方式，例如假设时延长度和隐层神经元的个数的最大取值分别取24和50，当时延长度和隐层神经元的个数分别取2和3时，对应的二进制编码为00010000011。

结合两种神经网络的性能评价指标以及适应度函数单调、连续的设计原则，本文设计的适应度函数为

式中:fiti为第i个NARX或者FTD神经网络的适应度函数；Errori为第i个NARX或者FTD神经网络的性能评价指标，其中NARX神经网络对应的指标为MAPE，FTD神经网络对应的指标为MAE。

在进行选择、交叉以及变异操作时，分别采用目前最为常用的轮盘赌选择、单点交叉以及基本位变异方法。

若相邻两代种群的平均适应度值的变化小于某一阈值，表示算法已经收敛，则退出算法。

4 短时多步预测双层模型工作流程

本文所设计的基于动态神经网络的SCATS线圈数据短时多步预测双层模型的在线应用流程如图3所示。由于交通参数的多步预测结果是确定可预测步数的数据基础，因此本文方法的标定流程是基于NARX神经网络的SCATS线圈数据多步预测方法在前，基于FTD神经网络的SCATS线圈数据可预测步数在线估计方法在后。在实际应用过程中，则应先估计目标交通参数在当前时间间隔的可预测步数，再对可预测步数内的交通参数进行估计。

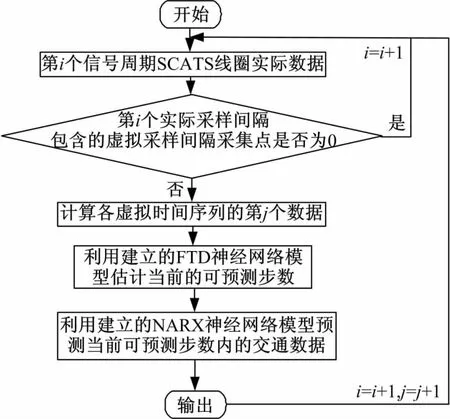
图3 本文方法的在线应用流程Fig.3 Online application process of proposed method

5 实验验证

5.1 数据来源

实证数据来源于国内某特大城市主干道的SCATS线圈，采样时间为2009年5月至7月，每天24h。实验区域为该主干道A、B、C连续3个交叉口，具体路线如图4所示。

图4 实验区域道路示意图Fig.4 Road map for experimental area

5.2 实验方案设计

利用文献［12］提出的虚拟时间序列构建方法，确定的SCATS线圈数据虚拟采样间隔时长为150s。因此，后续分析以150s时间尺度为例加以说明。

选取5月～6月内所有周一的数据作为标定集合，7月份所有周一的数据作为测试集合。在优化神经网络时，将标定数据集合再次随机分为训练样本、验证样本以及测试样本，依次占数据总数的70%、15%和15%。

短时多步预测结果的可接受误差阈值z应依据用户需求进行设定，本文参照文献［10］的方法确定为20%。为了更加充分地验证本文方法的有效性，在实验结果分析部分增加评价指标均方根误差 RMSE［13］。

在使用遗传算法优化神经网络结构时，本文借鉴被引用次数较多的文献［15］中的参数设置:种群规模设置为50，平均车头时距d最大取24，隐层神经元数N 最大取50，交叉率选为0.6，变异率选为0.0033，最大迭代次数选为100。

文献［9］提出了一种基于BP神经网络的交通数据多步预测方法，在进行多步预测时，采用的是固定预测步数。文献［10］以BP神经网络为基础，建立了交通数据序列的关联数据特征指标向量与可预测步数的关系模型，并采用移动平均法进行多步预测。本文将上述两个文献中的相应方法作为对比方法，分别对固定步数多步预测结果、可预测步数估计结果以及可变步数多步预测结果进行对比分析，以评价本文方法的有效性。

5.3 实验结果及对比分析

下面以交叉口B西进口线圈的周一数据集合为例，说明本文方法与对比方法的实验结果并进行分析。

5.3.1 固定步数时多步预测结果与分析

利用所设计的基于遗传算法的NARX神经网络结构优化方法，当平均车头时距和交通流量的 （d，N）分别为（6，13）和（12，15）时，即时延长度分别为6和12、隐层神经元数分别为13和15时，对应的NARX神经网络具有最佳性能。在选定的（d，N）下，该方法应用平均车头时距与交通流量的训练、验证及测试样本数据一步预测时的MAPE如表1所示。

表1 本文方法一步预测时的MAPETable 1 MAPE of one step forecasts using proposed method

以前述约定的测试数据集合为基础，分别采用文献［9］方法、文献［10］方法以及本文方法对平均车头时距和交通流量进行1～30步预测时，相应的MAPE和RMSE分别如图5和图6所示。

图5 3种预测方法平均车头时距1～30步预测结果对比Fig.5 Comparison of 1～30step forecasts for three forecasting methods of time headway

从图5和图6可以看出:

（1）平均车头时距和交通流量1～30步预测结果的MAPE、RMSE总体上呈递增的趋势，说明预测误差与预测步数之间存在一定的正相关关系。

（2）在对平均车头时距和交通流量进行1～30步预测时，参与比较的各种方法在预测误差方面存在明显且稳定的差异，本文方法的MAPE、RMSE最小，文献［9］方法和文献［10］方法的MAPE、RMSE相当，后者稍大，说明本文方法具有相对优势。

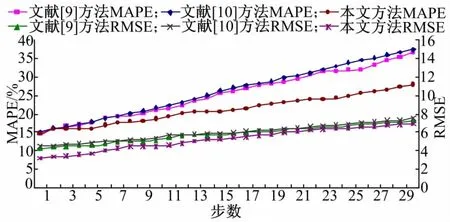
图6 3种预测方法交通流量1～30步预测结果对比Fig.6 Comparison of 1～30step forecasts for three forecasting methods of traffic flow

5.3.2 可预测步数在线估计结果及对比分析

利用所设计的基于遗传算法的FTD神经网络结构优化方法，当平均车头时距和交通流量的（d1，N1）分别为（6，16）和（8，15）时，即时延长度分别为6和8、隐层神经元数分别为16和15时，对应的FTD神经网络具有最佳性能。在选定的（d1，N1）下，该方法应用平均车头时距与交通流量的训练、验证及测试样本数据估计可预测步数时的MAE如表2所示。

表2 本文方法估计可预测步数时的MAETable 2 MAE of predictable steps estimation using proposed method

以前述约定的测试数据集合为基础，采用本文方法和文献［10］方法，对实验区域SCATS线圈数据的可预测步数进行估计，相应的误差指标如表3所示。

表3 本文方法与文献［10］方法可预测步数估计的 MAE、RMSETable 3 MAE and RMSE of predictable steps estimation for proposed method and literature［10］method

从表2和表3可以看出，本文方法在标定过程中表现出了良好的稳定性，而且基于测试数据集合的平均车头时距和交通流量可预测步数估计的MAE、RMSE都明显优于文献［10］的方法。

5.3.3 可变步数多步预测的结果及对比分析

为了对可变步数多步预测的效果进行评价，以测试数据集合为基础，计算全部时间间隔对应可预测步数内各步预测结果的总体MAPE、RMSE。

由于文献［9］没有涉及可预测步数的估计方法，在对其评价时，引入文献［10］和本文方法，并分别简称为文献［9］和文献［10］组合方法以及文献［9］和本文组合方法。相应方法的固定30步预测的效果与可变步数多步预测的效果如表4所示。

由表4可看出:

（1）平均车头时距和交通流量可变步数多步预测的MAPE、RMSE都优于对应方法的固定步数30步预测方法，说明进行可预测步数估计是非常必要的。

表4 固定30步预测效果与可变步数多步预测效果Table 4 Effects of fixed 30－step and dynamic multi－step forecasting for 3methods

（2）采用本文方法，平均车头时距和交通流量多步预测的 MAPE、RMSE均优于文献［9］与本文的组合方法，进一步表明了本文所设计的多步预测方法的有效性。

（3）采用文献［9］与本文的组合方法，平均车头时距和交通流量的MAPE、RMSE均优于文献［9］［10］的组合方法，进一步说明了本文所设计的可预测步数估计方法的有效性。

（4）在4种可变步数多步预测的方法中，本文方法的预测效果优于其他两种方法，表明本文所设计的双层模型能够进一步降低SCATS线圈数据短时多步预测的误差。

6 结束语

针对SCATS线圈数据的独特性，以动态神经网络为基础，设计了一种新的短时多步预测双层模型，并以我国某特大城市的实测数据为基础进行了验证和对比分析。结果表明，本文方法能够进一步降低SCATS线圈数据短时多步预测的误差。本文的研究成果有助于改善SCATS覆盖道路在交通信号控制、交通信息引导和交通指挥等方面的协调性。

［1］全永燊.城市交通控制［M］.北京:人民交通出版社，1989:226－236.

［2］彭信林，王宁鸣，周剑峰，等.SCATS数据采集系统的设计与实现［J］.计算机工程，2008，34（24）:256－260.Peng Xin－lin，Wang Ning－ming，Zhou Jian－feng，et al.Design and implementation of data collection system on SCATS［J］.Computer Engineering，2008，34（24）:256－260.

［3］姜桂艳.道路交通状态判别技术与应用［M］.北京:人民交通出版社，2004:114－119.

［4］姚智胜，邵春福，熊志华，等.基于主成分分析和支持向量机的道路网短时交通流量预测［J］.吉林大学学报:工学版，2008，38（1）:48－52.Yao Zhi－sheng，Shao Chun－fu，Xiong Zhi－hua，et al.Short－term traffic volumes forecasting of road network based on principal compontent analysis and support vector mochine［J］.Journal of Jilin University（Engineering and Technology Edition），2008，38（1）:48－52.

［5］Li C X，Anavatti S G，Ray T.Short－term traffic flow prediction using different techniques［C］∥The 37th Annual Conference of the IEEE Industrial Electronics Society，Melbourne，2011:2423－2428.

［6］Gao S，Zhang Z Y，Cao C G.Road traffic freight volume forecast using support vector machine combining forecasting［J］.Journal of Software，2011，6（9）:1680－1687.

［7］Smith B L，Williams B M，Oswald R K.Comparison of parametric and nonparametric models for traffic flow forecasting［J］.Transportation Research，Part C:Emergence Technology，2002，10（4）:303－321.

［8］Hosseini S H，Moshiri B，Rahimi－Kian A，et al.Short－term traffic flow forecasting by mutual information and artificial neural networks［C］∥IEEE International Conference on Industrial Technology，Athens:IEEE，2012:1136－1141.

［9］Dougherty M S，Cobbet M R.Short－term inter－urban traffic forecasts using neural networks［J］.International Journal of Forecasting，1997（13）:21－31.

［10］姜桂艳，常安德，牛世峰，等.基于BP神经网络的交通数据序列动态可预测性分析方法［J］.北京工业大学学报，2011，37（7）:1019－1026.Jiang Gui－yan，Chang An－de，Niu Shi－feng，et al.Dynamic predictability analysis for traffic data serials based on BP neural network［J］.Journal of Beijing University of Technology，2011，37（7）:1019－1026.

［11］Pisoni E，Farina M，Carnevale C，et al.Forcasting peak air pollution levels using NARX models［J］.Engineering Applications of Artificial Intelligence，2009，22:593－602.

［12］姜桂艳，李琦，常安德，等.基于SCATS线圈数据的交通状态在线定量评价与预测方法［P］.中国专利:CN101739814A，2010－06－16.

［13］薛薇.SPSS统计分析方法及应用［M］.北京:电子工业出版社，2004:113－115.

［14］Htike K K，Khalifa O O.Rainfall forecasting models using focused time－delay neural networks［C］∥International Conference on Computer and Communication Engineering，Kuala Lumpur， Malaysia，2010:1－6.

［15］Arifovic J，Gençay R.Using genetic algorithms to select architecture of a feedforward artificial neural network［J］.Physica A:Statistical Mechanics and its Applications，2001，289（3－4）:574－594.