基于PSCAD的双馈风力发电系统DTC策略研究

李生民，何欢欢，胡丁尹

（西安理工大学 自动化与信息工程学院，陕西 西安 710048）

1 引言

近年来，双馈电机在风力发电中得到越来越广泛的应用，但是由于双馈电机的动态数学模型是一个高阶、非线性、强耦合的多变量系统［1］，控制比较复杂，而矢量控制根据坐标变换，把交流电机的定子电流转换成同步旋转坐标系下正交的励磁分量和转矩分量，最终实现了励磁分量和转矩分量的解耦控制［2］，简化了控制方案。但是矢量控制用于实现解耦控制的前馈补偿相中包含有电机参数，而且矢量控制系统为了获得期望的闭环动态响应所用到的PI控制器的系数选取依据于电机参数的计算［3］，因此，矢量控制对电机参数的依赖性较高。而且电机参数在实际运行过程中容易发生变化导致矢量控制的抗干扰能力较差。

为了解决矢量控制对电机精确参数的依赖性，文献［4-5］将直接转矩控制技术应用于双馈异步电机中。直接转矩控制不需要通过间接的控制变量（电流和磁链来控制转矩），而是根据磁链和电磁转矩滞环比较器的逻辑输出，在预先设计好的表格中选取对应的转子电压矢量，来控制双馈风力发电机的磁链和电磁转矩［6］。直接转矩控制无需经过冗长复杂的数学坐标变换，具有动态性能稳定、响应速度快、结构简单和不依赖电机参数等优点［7］。因此，直接转矩越来越受到人们的关注。

本文将直接转矩控制策略应用到双馈风力发电机系统中，根据转子磁链和电磁转矩滞环比较器的逻辑输出以及扇区编号，在预先设计的表格中得到最优开关矢量并且将该矢量作用于转子绕组，达到对电磁转矩和转子磁链幅值的快速控制，实现最大风能捕获和满足电网的无功需求。

2 双馈风力发电基本原理

双馈风力发电系统主要由风力机、双馈异步发电机、双PWM背靠背式变流器以及电网组成。由图1所示，双馈电机的定子侧直接与电网相连接，转子侧和变流器相连接，通过调节转子绕组的三相励磁电流来控制定子侧输出恒定频率的电流，确保电能输出质量。其中定子电流幅值的大小决定了输出功率的大小、相位决定输入的功率因数。

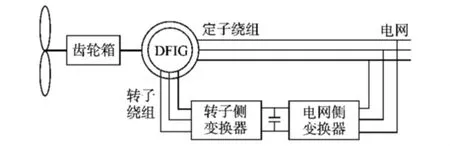
图1 双馈风力发电系统基本构成Fig.1 The basic structure of doubly fed wind power generation system

根据双馈异步发电机定子绕组与转子绕组产生的旋转磁场相对静止的原理，可以得出变速恒频风力发电机组运行时转速和定子绕组、转子绕组电流频率关系的数学表达式［8］：

式中：nr为转子转速；f1为定子电流频率；f2为转子电流频率；pn为发电机的极对数。

当转子转速为nr时，由变频器控制转子电流的频率f2来维持定子电流频率f1恒定，即保证f1为电网的工频频率，实现了整个风电系统的首要目标：变速恒频。依据电机交流调速系统里面的直接转矩控制就可以得到很好的实现。

3 直接转矩控制原理

双馈电机直接转矩控制原理是指电机定子绕组与电网相接，对转子绕组进行控制。在控制方法上采用转子磁链幅值及电磁转矩的参考值分别和它们的观测值做滞环比较，然后通过最优开关矢量表选择转子侧逆变器功率器件的开关状态来实现对电机转矩的直接控制。根据直接转矩控制的特点，双馈风力发电机的数学模型应建立在转子旋转d-q坐标系中，基本方程如下：

电压方程

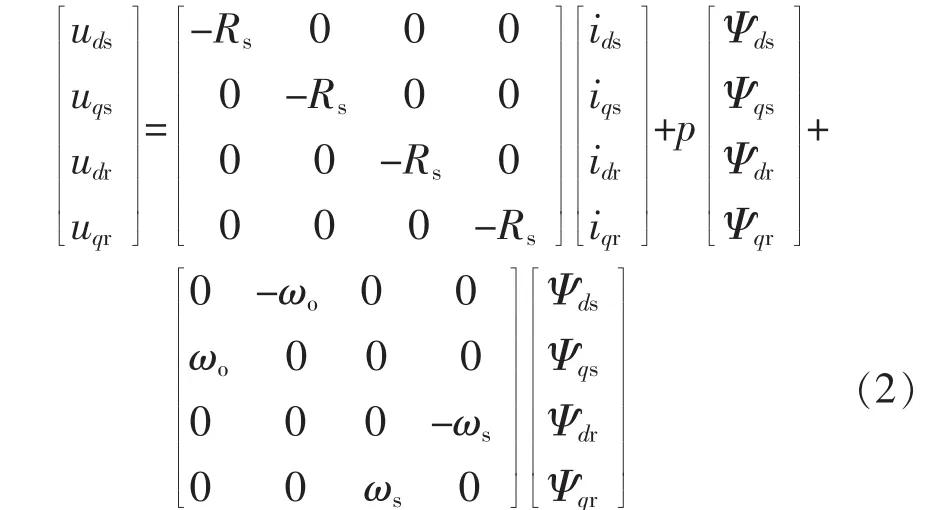
磁链方程为

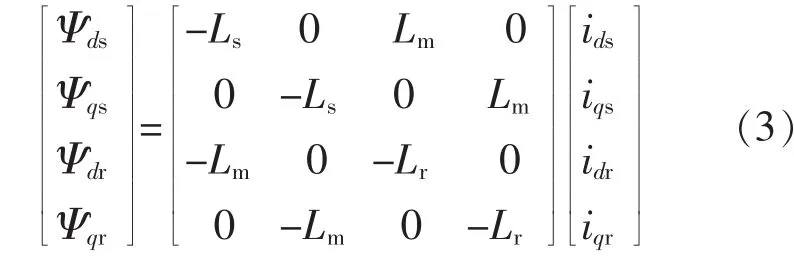
电磁转矩方程为

式中:Ψs为定子磁链矢量；Ψr为转子磁链矢量；θsr为定子磁链矢量和转子磁链矢量之间的夹角。

式（4）即为直接转矩控制在双馈发电机电磁转矩控制应用的理论依据。不难看出，在定子磁链矢量、转子磁链矢量的模值均保持不变的情况下，通过施加不同的转子电压矢量，使得转子磁链在期望的方向上改变，即能够改变定转子磁链矢量之间的夹角，实现对电磁转矩控制的目的［9］。因此，通过控制逆变器输出电压矢量来实现对电磁转矩的快速调节。

4 直接转矩控制策略的实现

双馈电机DTC控制策略是基于转子磁链轨迹为圆形的控制策略。它将逆变器输出的电压矢量在360°空间按照一定的规律进行6等分，每一等份空间称之为一个扇区。在每一个扇区里选择一定数目的对转子磁链幅值、转矩有影响效果的电压矢量。表1为每一个扇区中的电压矢量对电磁转矩和转子磁链幅值的控制效果。该表称为最优开关矢量表 （简称为开关表），如表1所示。

表1 电压矢量查询表Tab.1 Voltage vector look-up table

表1中，变量Ψ为磁链滞环比较器输出变量、τ为转矩滞环比较器输出变量、θn为扇区编号。该最优开关矢量表，兼顾了转子磁链幅值和电磁转矩的同时控制。而要获得转子磁链幅值和电磁转矩控制需求，可以将转子磁链幅值和电磁转矩误差分别送到各自的滞环比较器中，即可获得一个标识转子磁链幅值和电磁转矩控制需求的开关变量。若已知系统对转子磁链幅值和电磁转矩控制的需求，例如转矩增大1、减小-1、不变0，则根据这些需求就可以在最优开关矢量表中查找获得一个最优开关矢量。

从表1中可知，只要知道转子磁链目前所在位置和转子磁链大小、输出转矩的所需变化方向，就可通过查表法得到要施加电机的电压矢量［10］。

对于转子磁链大小，输出为两电平，因此使用两电平滞环比较器。其函数表达式如下：

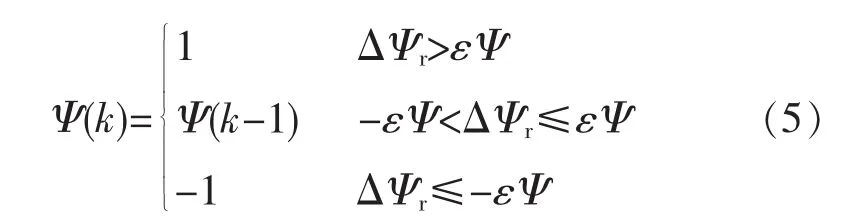
式中：Ψ(k-1)和Ψ(k)为前一时刻和当前时刻的滞环比较器输出值；输出值中1为增加，-1为减小；ΔΨr为转子磁链大小的指令值与实际值差，；εΨ 为 ΔΨr的允许偏差 （滞环比较器的阈值）。

对于输出转矩，输出为三电平，因此使用三电平滞环比较器。其函数表达式如下：

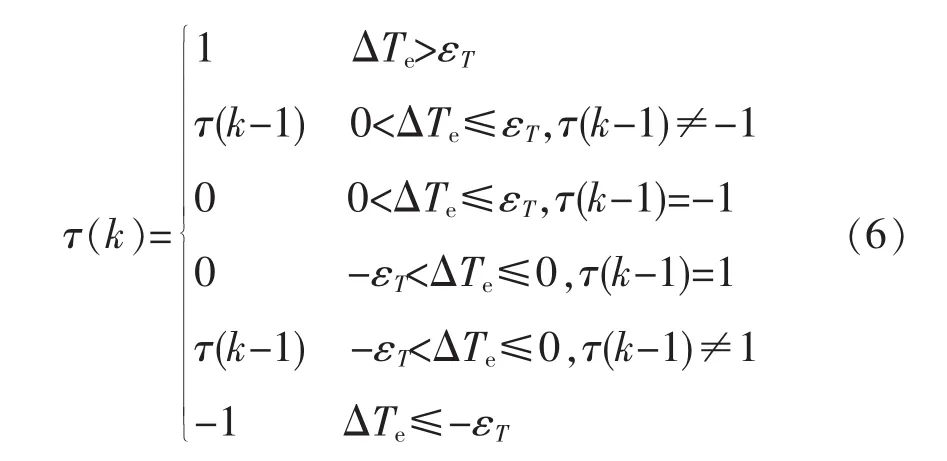
式中：τ(k-1)和τ(k)分别为前一时刻和当前时刻的输出转矩滞环比较器输出值；输出值中1为增加、0为维持不变、-1为减小；ΔTe为输出转矩的指令值与实际之差，；εT为 ΔTe的允许偏差（滞环比较器的阈值）。

图 2给出了对应于式（5）和式（6）的两种滞环比较器的控制规则。其中图2a为转子磁链大小控制器，是输出值为1或-1的两电平滞环比较器；图2b为输出转矩控制器，输出值为1，0，-1的三电平滞环比较器。

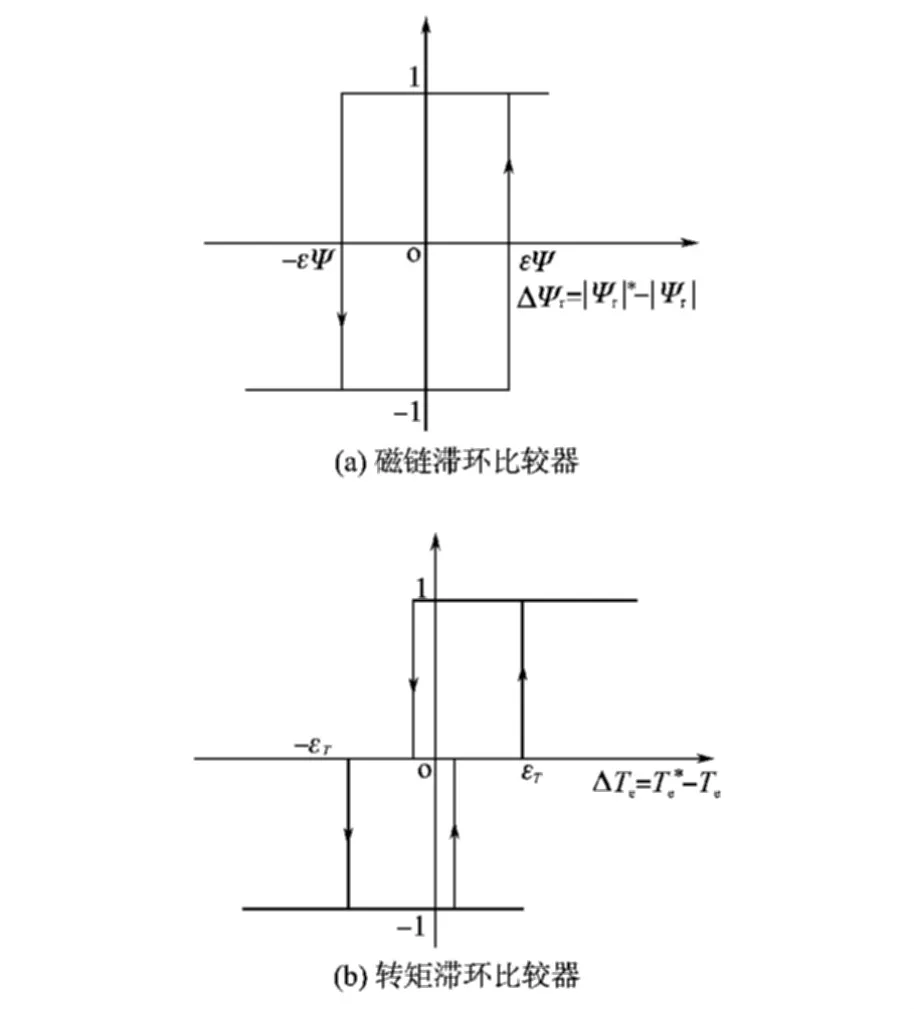
图2 滞环比较器Fig.2 Hysteresis comparator

5 双馈电机直接转矩控制系统

双馈电机直接转矩控制系统如图3所示。双馈风力发电直接转矩控制系统首先检测双馈电机的实际转速，然后使其和给定转速相比较后，通过转速PI调节器输出电磁转矩给定值，其值与观测到的电磁转矩比较后的误差值送给转矩滞环比较器输出变量τ；根据电网需求给定无功功率为0，与功率反馈值Qs比较后经PI功率调节器运算然后使其与反馈的转子磁链幅值比较后的误差值送给磁链滞环比较器输出变量Ψ；根据转子电压检测值计算出转子磁链矢量所处的扇区编号θn；最后根据τ，Ψ，θn查表1得到一个最优开关矢量，该矢量作用于转子绕组，实现对电磁转矩和转子磁链幅值的快速控制，实现最大风能捕获和满足电网无功需求。

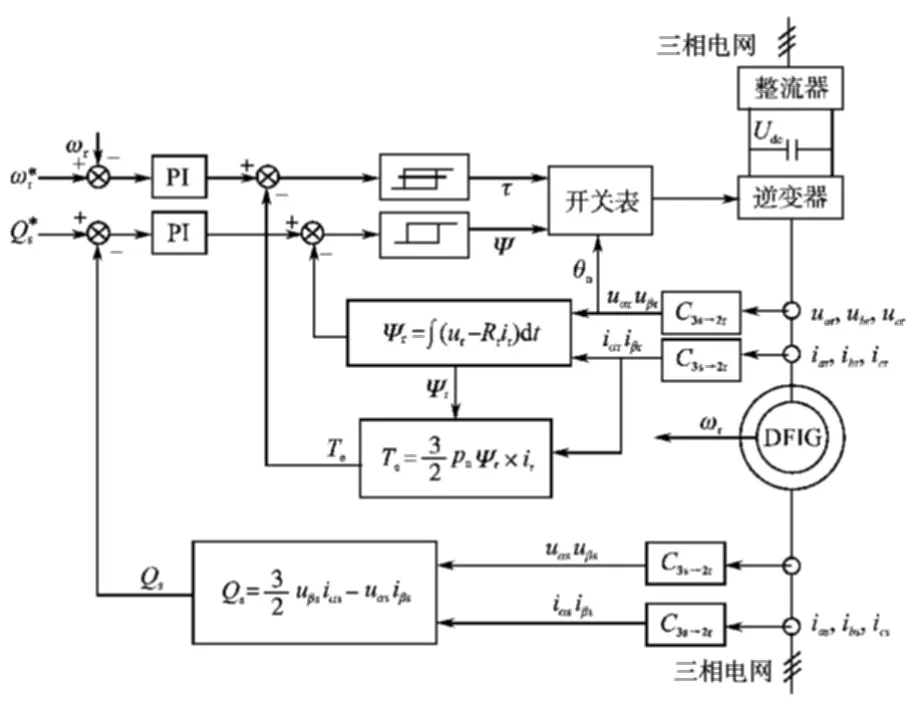
图3 双馈风力发电系统直接转矩控制框图Fig.3 Doubly-fed wind power systems directtorque controldiagram

6 仿真模型建立及结果分析

本文用电力系统仿真软件PSCAD/EMTDC对1台40 kW发电机组的动态模型进行仿真分析，双馈风力发电参数为：额定功率Pn=40 kW，额定电压Un=690 V，额定频率fn=50 Hz，定子电阻Rs=0.340Ω，转子电阻Rr=0.315Ω，定子自感Ls=0.0438 H，转子自感Lr=0.045 H，定转子互感Lm=0.043 H，转动惯量J=0.09，极对数pn=3。

仿真过程：电机启动到0.3 s以前，给定1（标幺值）的额定转矩，0.3 s以后，电机给定基本风速为8 m/s的随机风速时的转矩，其中地表粗糙系数为0.0192，扰动范围为600 m。

根据PSCAD/EMTDC中提供的风源模型，输出基本风速为8 m/s的随机风速。风速波形如图4所示。

图4 风速曲线图Fig.4 Wind speed curve

图5为电机实际转速曲线图，电机启动0～0.3 s内，给定电机的额定转矩为1（标幺值），0.3 s以后，电机转速经过短暂的调节，可以很好地跟随风速的变化而变化。图5说明双馈电机在直接转矩控制策略下的反馈转速能够很好地跟随最佳电机转速，从而实现风能最大功率点跟踪的控制要求。

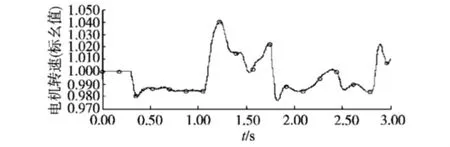
图5 电机转速实测值曲线图Fig.5 The motor speed measured curve

图6为电磁转矩和机械转矩曲线图。由图6可知，发电机的电磁转矩Te存在波动较大，这是因为风能追踪采用的是直接转矩控制策略，在风速变化的同时，发电机控制系统需要不断控制调整电磁转矩，从而跟踪转速变化，实现变速恒频运行，可以看到这种控制策略使系统的动态响应比较快。图7和图8为定子三相电流波形及局部放大图。

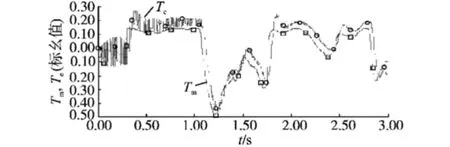
图6 电磁转矩和机械转矩曲线图Fig.6 The electromagnetic torque and mechanicaltorque curves

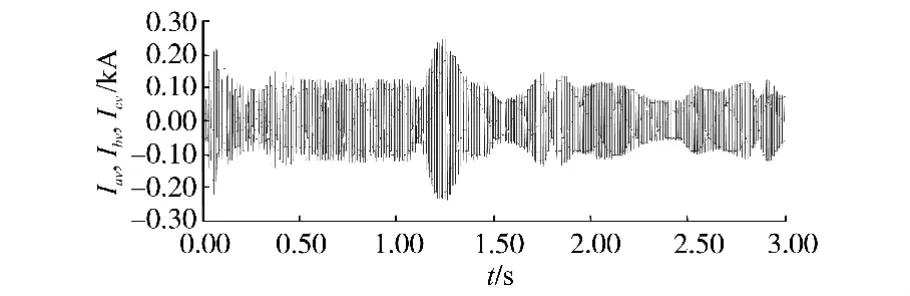
图7 定子电流曲线图Fig.7 The waveforms of stator current curves

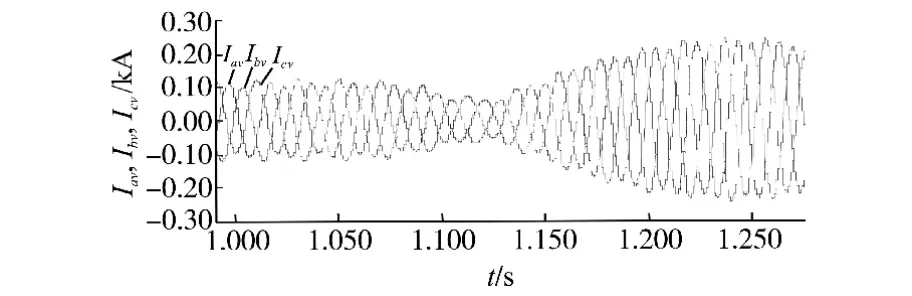
图8 定子电流局部放大曲线图Fig.8 Detail view of the waveforms of stator current curves

随着风速的不断变化，发电机定子侧电流只是幅值发生相应的变化，而其频率却不受风速变化，始终保持着恒频50 Hz，说明采用直接转矩控制策略的风力发电系统实现了变速恒频和最大功率点输出控制。

图9为定子有功功率和无功功率曲线图。

图9 定子有功和无功功率曲线图Fig.9 Stator active and reactive power curves

由图9可知，定子绕组电流的幅值变化时，有功功率也发生相应的变化，而无功功率在很小的范围内基本保持不变，表明了双馈电机在实现最大功率点跟踪的同时实现了有功和无功功率的解耦控制。

图10为转子三相电流曲线图，表示转子侧励磁三相电流的频率和幅值随风速的变化而变化。转子侧电流频率的不断变化是为了确保定子电流频率保持恒定。

图10 转子三相电流曲线图Fig.10 Three-phase rotor current curves

图11a为系统给定随机风速时的转子磁链轨迹；图11b为系统给定恒定风速时的转子磁链轨迹。由图11可知，转子磁链在0.3 s以后，其轨迹在不同的坐标下基本趋于圆形，电机可以平稳运行。

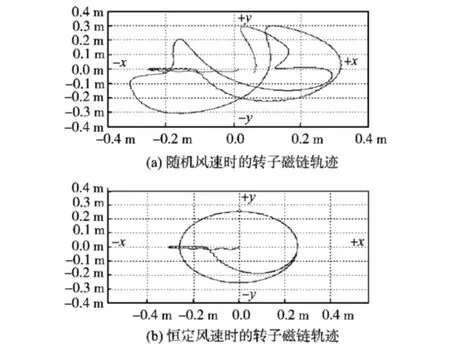
图11 转子磁链轨迹Fig.11 Track of rotor flux linkage

由上述波形分析表明：该系统的响应速度快，动态性能优越，充分验证了控制策略的正确性和可行性。

7 结论

直接转矩控制策略鲁棒性强、转矩动态响应速度快、控制结构简单，本文将直接转矩控制策略应用在双馈风力发电机系统中，实行电磁转矩和转子磁链的砰-砰控制来选择电压空间矢量和逆变器的开关状态。并在PSCAD仿真环境下搭建了其系统模型，仿真结果表明，双馈风力发电系统直接转矩控制策略使得这个庞大而又复杂的系统能较快的响应系统输入，在风速发生变化时，实现了有功功率和无功功率的解耦控制，最终达到了最大功率点跟随控制，满足了电网的无功需求。验证了理论分析控制系统的正确性和有效性。

［1］陈伯时.电力拖动自动控制系统［M］.北京：机械工业出版社，2003.

［2］Bolognani S， Zigliotto M.Novel Digital Continuous Control of SVMInvertersin the Overmodu l ation Range［J］.Industry Applications， IEEE Transactions， 1997， 33（2）： 525-530.

［3］Xu L，Cartwright P.Direct Active and Reactive Power Control of DFIG for Wind Energy Generation［J］.IEEE Transactions on Energy Conversion， 2006， 21（3）： 750-758.

［4］马小亮，刘志强.双馈电动机直接转矩控制技术的研究［J］.电工技术学报，2003，18（5）： 63-68.

［5］Xing Z X，Yao X J， Sui H X，et al.DTC in Doubly-fed VSCF W ind T urbine C ontrol S ystem ［C］∥Proceedings of the IEEE International Conference on Industrial Technology，2006：2715－2718.

［6］Shi J， Fengge Z.Research on Maximal Power Tracking Control for Brushless Doubly-fed W ind P ower G enerator B ased on DTC ［C］∥International Conference on Electrical Machines and Systems，2011：20－23.

［7］徐艳平，钟彦儒.基于占空比控制的永磁同步电机新型直接转矩控制策略［J］.电工技术学报， 2009， 24（10）： 27－32.

［8］鲍薇，尹忠东，任智慧.变速恒频双馈风力发电机组交流励磁控制系统研究［J］.电气传动， 2010， 40（1）： 27－32.

［9］Nik Rumzi Nik Idris，Abdul Halim Mohamed Yatim.Direct Torque Control of Induction Machines with Constant Swithing Frequency and Reduced Torque Ripple［J］.IEEE Transaction on Power Electrnics，2004，51（4）：758－767.

［10］李亚林，李含善，任永峰，等.变速恒频风力发电系统的仿真研究［J］.电力科学与工程，2007，23（3）：l－5.