基于FPGA的FIR数字滤波器算法的改进及仿真＊

韩 建，何学兰，魏运峰

（1.东北石油大学 电子科学学院，黑龙江 大庆 163318；2.东北石油大学 黑龙江省高校校企业共建测试计量技术及仪器仪表研发中心，黑龙江 大庆 163318）

引 言

基于有限长单位冲激响应滤波器（FIR）的稳定性和线性相位的优点，FIR滤波器有着更为广泛的应用。目前，实现数字滤波器的方法主要有软件实现和硬件实现。软件实现的方法简单，但是实时性差。硬件实现的方法有数字信号处理器（DSP），专用集成电路和现场可编程门阵列（FPGA）等［1］。DSP实现数字滤波器方法灵活，开发周期短，但其软硬件的结合方式限制了滤波处理速度，不适合用在实现实时性较高要求的系统。ASIC器件可靠性高，实时性好，但灵活性差，不适合科研和开发。FPGA器件结合了上面两种器件的优点，具有很好的实时性，可靠性和灵活性，因此研究基于FPGA的数字滤波器的实现对于工程应用有重大的意义［2］。

本文采用FPGA技术，应用硬件描述语言实现数字滤波器。基于FIR数字滤波器的分布式算法提出改进算法，此算法不但不需使用乘法器而且减小了存储器的使用数量，大幅度节约了硬件资源且可实现高速滤波。

1 FIR滤波器的改进算法实现

1.1 算法推导

FIR滤波器的输入信号和输出信号的关系为：

为了方便说明，假设y＝y（n），xi＝x（n－i），则：

假设xi为k位二进制数据，它可以写成以下形式：

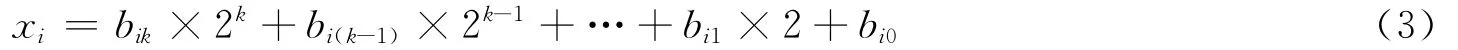
其中，bik为xi的第k位，将式（3）代入式（2）可以得到：

为了实现算法，可以定制一个ROM存储h0，h1，h2，…，hN－1的可能组合的和。对应一个N阶的FIR数字滤波器，该ROM中地址和数据的对应关系如表1所示。

根据式（4）可以知道，要得出FIR滤波器的输出，首先需要一个初始存储全为0且长度为滤波器阶数的队列将输入的数据存入队列［3］。以队列中每个数据对应的位组合为一个地址，在ROM中查出对应的值乘上位权值相加就可以得到输出值。

1.2 算法实现

该算法可以用并联和串联来实现。串行结构如图1所示，该结构是将保存在队列中的输入分别送入一组向右移位寄存器，移位寄存器的最右边的一位组合成地址在ROM中查出对应值，送入累加器。当下一个时钟上升沿，移位寄存器组向右移一位，最右边一位组成的新的地址在ROM中查出数据，再进行累加。但是，如果数据是8位的，则要8个时钟周期才能输出一个数据，时钟的频率必须是采样频率的8倍，串行结构难以实现高速FIR滤波器［4］。

表1 ROM表中数据Tab.1 Data in ROM table

图1 串联型分布式算法实现硬件结构Fig.1 Hardware structure implement based on series distributed computation

图2 流水线加法器的硬件结构Fig.2 Hardware structure of pipeline adder

当数据为8位，并型结构需要相对串型结构的8倍的硬件资源。并型结构需要8个相同的ROM，所有数据每一对应位组成的地址分别在8个ROM中查询，再乘以权值，最后用流水线加法器相加。流水线加法器的结构如图2所示，并联型分布式算法的硬件实现如图3所示。

图3 并联型分布式算法的硬件实现Fig.3 Hardware structure implement based on parallel distributed computation

1.3 分布式算法的改进

分布式算法不需要使用乘法器，降低了硬件资源的使用，但是却对ROM的容量提出了很高的要求［5］。假设要实现一个 N 阶的 FIR滤波器，系数h0，h1，h2，…，hN－1的组合的和可能性有2N中，对于并联型的分布式结构，ROM的容量需8×2N×Mbit，其中8为输入数据位宽，M为系数量化位数。运用该算法实现低阶FIR滤波器时，消耗的存储器较少，然而随着阶数不断升高，存储器的消耗呈指数增长，在实现高阶FIR滤波器时，这种算法将消耗过多存储单元，而在实际应用中FIR滤波器的阶数一般都比较高，所以需考虑对分布式算法进行改进。

因为倍数增长比指数增长慢，因此改进算法是：将高阶FIR数字滤波器结构转变成多个低阶FIR数字滤波器分布式算法结构的组合。

本文设计滤波器的阶数是64阶，8的倍数，式（4）可以写成如下形式：

其中8m＋7＝N－1，这样把N个滤波器系数分成N／8组，每组可利用8阶FIR滤波器的并联型分布式算法结构实现，最后用流水加法器相加得到结果。实现框图如图4所示，整个系统需要（N／8）这样的8阶FIR滤波器分布式算法结构，最后将输出的数据用流水线加法器相加［6－7］。

这样，采用改进算法需要用到的存储器为M×8×（N／8）×28bit，相对于采用传统的并联分布式算法需要消耗的存储单元为8×M×2Nbit，改进算法大幅减少了存储器的使用。

根据以上分析，本文设计的FIR数字滤波器为64阶，输入数据量化为8位，系数量化为13位。所以采用传统的并联分布式算法需要消耗存储单元8×264×13bit，而采用改进算法只需要消耗存储单元13×8×8×28bit，相对于传统算法，存储器使用减少了253倍［8］。

图4 8的倍数阶数的FIR滤波器的实现框图ig.4 Block diagram of implementation multiple of 8order FIR filters

2 改进算法的仿真验证

用Verilog HDL结合分布式改进算法编写器程序实现FIR滤波器。在这个仿真中，输入正弦波的频率为300kHz、500kHz和600kHz采样频率。本文中FIR滤波器是64阶低通滤波器，采样频率为4MHz，通带截止频率为500kHz，阻带截止频率为600kHz，仿真结果如图5所示。输入和输出的波形均符合正弦函数，输入输出波形的衰减情况初步表明滤波器显现出低通特性。

图5 输入不同正弦的采样频率时FIR滤波器的输出波形Fig.5 Output wave form based on different sampling frequency

表2是仿真值与理论值的比较表，由此可见改进算法实现的FIR滤波器和FDA tool设计出的滤波器对信号的衰减基本一致，误差在合理范围内。

表2 FIR滤波器仿真与理论设计幅度数据的比较Tab.2 Comparison amplitude data of theoretical and simulation of FIR filter

3 结 论

在现代电子系统中，FIR数字滤波器以其良好的线性特性被广泛使用，属于数字信号处理的基本模块之一，本文使用FPGA对FIR滤波器进行硬件的实现，在分析分布式算法的基础上提出了改进算法，解决了分布式算法占用大量存储器空间的问题，提高了硬件资源的使用率和运算速率。通过仿真验证进一步证明了该算法的正确性。为进一步提高数字滤波器的精度和速率打下了基础。

［1］赵 洁，王大勇，李 艳，等.数字全息术应用于生物样品相衬成像的实验研究［J］.中国激光，2010，37（11）：2906－2911.

［2］李锦明，谢绪煜，马游春，等.基于FPGA的FIR滤波器系统的设计［J］.化工自动化及仪表，2011，34（8）：44－48.

［3］于瀛洁，郭 路，周文静.数字全息位相拼接实验研究［J］.光学仪器，2011，33（4）：55－59.

［4］葛 鹏，刘 涛，李 奇，等.基于FPGA＋ADSP的线阵CCD非接触测量系统［J］.光学仪器，2008，30（5）：1－4.

［5］王东旭，潘广祯.MATLAB及其在FPGA中的应用［M］.北京：国防工业出版社，2006.

［6］毛 磊，李 勇，马利红，等.显微数字全息图相位的滤波法提取［J］.光学仪器，2012，34（4）：16－20.

［7］吴黎慧，蒲南江，高 磊，等.基于FPGA的FIR滤波器的误差分析［J］.电子测试，2011，34（8）：56－58.

［8］胡同花，周维龙.基于FPGA的 OFDM 调制器设计与实现［J］.电子设计工程，2011，29（15）：9－12.