细胞毒性试验多孔平行数据异常值检验方法的比较

管 莹，夭建华，朱洲海，米其利，曾婉俐，黄海涛，高 茜，李雪梅

（云南烟草科学研究院，云南 昆明650106）

生物实验中为了实现高通量的测定，常以多孔板作为实验的工具载体，其检测体系可低至微升级样品量，通量可扩充至1536孔板。该检测手段使得研究者可以在一次试验中获得多个平行检测数据，但伴随着通量的提高，检测体系的体积相应减小，较小的检测体系的稳定性也有所下降。细胞毒性试验作为一类重要的体外实验，广泛应用于评定食品、药品、化妆品对细胞的毒性作用［1－3］。该试验是将受试物加入到种植有受试细胞的96孔细胞培养板中，通过检测受试物对细胞存活率的影响，来判定受试物的细胞毒性。由于在将受试细胞种植到96孔细胞培养板的过程中，很难保证接种到每孔中的细胞数量和状态完全一致，可能会导致在同一批平行检测的数据中有个别数据与其它数据明显不一致，这种数据称为异常值，也称为异常数据或离群值［4］。实际运用中，当检测数据中存在与其它检测值差异较大的数据时，应首先排除检测过程中操作技术、仪器故障、数据计算、笔误等产生的误差［5］。未经正式统计分析处理就将主观上认为异常的值任意舍弃的做法是不可取的，这样做表面上得到了分散很小、精密度很高的结果，但实质上可能降低了重复测量得到的平均值的准确度，以相同条件再次检测时，超过该误差指标范围的“异常值”必然还会再次出现。

如何评估检测数据的准确性是统计学研究的重要课题，也是当前检测工作中普遍关心的问题。选取适当的异常值检验方法对数据进行分析就尤为重要。鉴于此，作者对常用的5种异常值检验方法的适用情况及对同一组细胞毒性试验数据异常值的检出进行了比较研究，以期为相关科研工作者选取适当异常值检验方法提供依据。

1 异常值的判别方法［6］

1．1 拉依达（Pauta）准则

拉依达准则又称3σ准则，该准则检验数据基于正态分布，根据正态分布理论｜vd｜≤3σ的概率为99．7%，因此在有限检测中，某次检测值的误差大于3σ的几率仅为0．3%，则认为该检测值为粗大误差值的异常值，需剔除。

当检测次数n较大时，该准则简单易行，是比较实验中的常用方法。但当n不太大时，检测数据中即使存在误差较大的异常值也很难被检出，由于贝塞尔公式意味着≤3σ，异常值无法检出。

由此表明，当重复检测值较少时，不宜使用拉依达准则，特别是当n≤10时，拉依达准则完全无法检出异常值。但样本量较大时，用拉依达准则对检测数据的异常值进行初筛最为简便［7］。

1．2 肖维勒（Chauvenet）准则

肖维勒准则也是以数据呈正态分布为前提。假设多次重复测量所得的n个检测值中，某个检测值的残余误差｜ΔXi｜＞Zcσ，则剔除此数据。其中Zc是样本容量为n时的判别系数，可以由Zc值表获取。肖维勒准则在一定程度上弥补了拉依达准则的不足，可以用于n≤10时对异常值进行判定。相对于拉依达准则，肖维勒准则更为严格。

1．3 格拉布斯（Grubbs）准则

格拉布斯准则与肖维勒准则相似，但判定系数不同。格拉布斯准则中假设多次重复测量所得的n个检测值中，当某个检测值的残余误差｜ΔXi｜＞T0σ，则剔除此数据。T0是样本容量为n时的判别系数，可以由T0（n，α）值表获取，与肖维勒准则中Zc值判定系数不同的是T0值与重复测量次数n和置信概率α均相关，格拉布斯准则概率意义更为明确。格拉布斯准则也要求检测数据呈正态分布。

1．4 狄克逊（Dxion）准则

狄克逊准则也是以数据呈正态分布为前提，通过极差比判定和剔除异常数据。假设有一组测量数据，从小到大依次排列有X1≤X2≤…≤Xn，且为正态分布，则可能为异常值的检测数据必然出现在两端，即X1或Xn。与一般比较简单极差的方法不同，狄克逊准则为了提高判断效率，对不同样本量应用不同的极差比公式进行计算，见表1。

表1 不同样本量对应的极差比公式Tab．1 Formula of different sample sizes

在确定检验水平α后查表得出临界值D1－α（n），分别检验高端值 Dn和低端值 D′n，当 Dn＞D1－α（n）或D′n＞D1－α（n）时判定 Xn或 X1为异常值，反之则无异常值检出。

1．5 罗马诺夫斯基（t检验）准则

罗马诺夫斯基准则也是将最小检测数据与最大检测数据分别进行检验，如｜X1－｜＞K（n，α）σ′或｜Xn－｜＞K（n，α）σ′则判定X1或Xn为异常值。式中X′和σ′分别为不包含X1或Xn的n－1个数据的均值和标准差；K（n，α）为临界值，其中n为样本容量、α为置信度，K（n，α）值可通过查表获得。

这种检验方法是将X1或Xn暂时删去后进行计算，这样既保证σ′的正确性又保证了其独立性。

2 各准则检验步骤及应用实例

表2给出的测量数据为本实验室某次MTT细胞毒性试验细胞对照组的16个平行孔于490nm波长下检测的吸光值。以下分别用拉依达准则、肖维勒准则、格拉布斯准则、狄克逊准则、罗马诺夫斯基准则对该组数据进行检验，判断是否存在异常值。

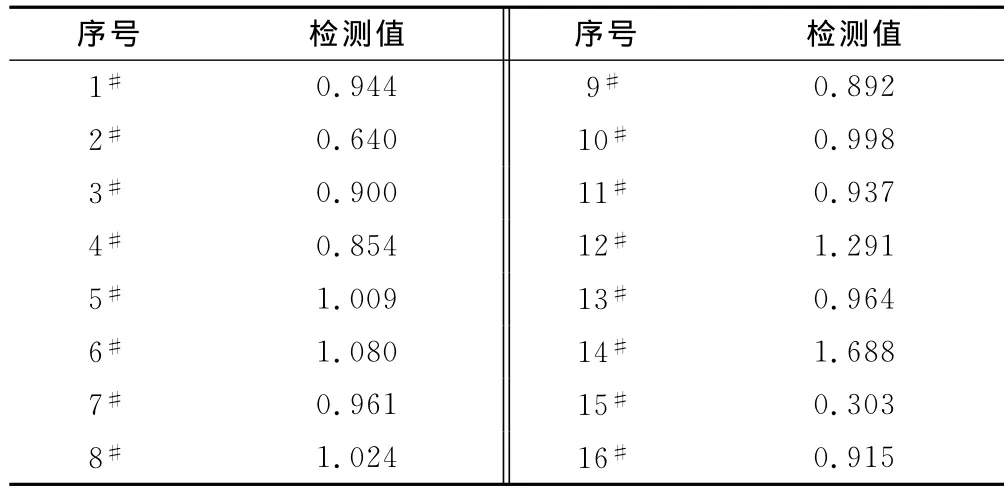
表2 细胞毒性试验同一剂量平行孔测量结果Tab．2 Detection results of cytotoxicity parallel

2．1 拉依达准则检验步骤及结果

（1）计算算术平均值：

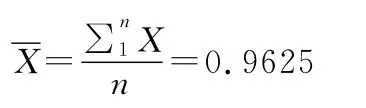
（2）计算剩余误差及3倍标准偏差σ：

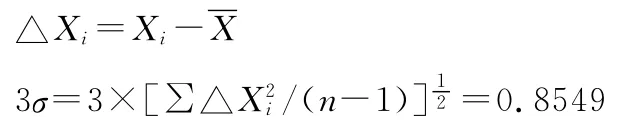
（3）计算结果表明，16个检测值中14＃测量值剩余误差最大，为0．7255，但仍小于3σ（0．8549），根据拉依达准则该组数据中无异常值。

2．2 肖维勒准则检验步骤及结果

（1）计算算术平均值：

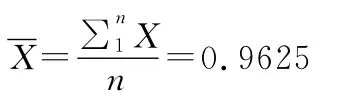
（2）计算剩余误差及标准偏差σ：

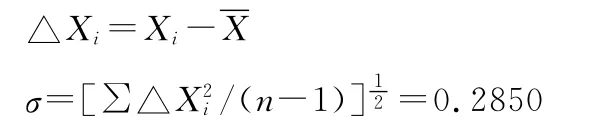
（3）对应Zc值表，当样本量n＝16时对应的Zc值为2．15，故Zcσ＝2．15×0．2850＝0．6127。

（4）计算结果表明，16个检测值中14＃、15＃测量值剩余误差分别为0．7255、0．6595，均大于Zcσ（0．6127），根据肖维勒准则该组14＃、15＃测量数据1．688、0．303为可疑值，任意选择剔除其中一个值后继续检测，本例中首先剔除1．688。

（5）根据上述步骤继续对剩余15个数据进行检验，检出可疑值0．303、0．640、1．291，任意选择剔除其中一个值后继续检测，本例中首先剔除0．303。

（6）根据上述步骤继续对剩余14个数据进行检验，检出可疑值0．640、1．291，任意选择剔除其中一个值后继续检测，本例中首先剔除1．291。

（7）根据上述步骤继续对剩余13个数据进行检验，检出可疑值0．640，剔除后继续检测。

（8）根据上述步骤继续对剩余12个数据进行检验，无异常值检出。

根据肖维勒准则共剔除4个异常值，分别为0．303、0．640、1．291、1．688。

2．3 格拉布斯准则检验步骤及结果

（1）确定置信概率α为0．05。（2）计算算术平均值：

（3）计算剩余误差及标准偏差σ：

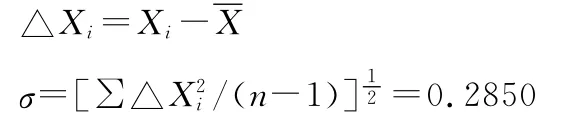
（4）查表获得T0（16，0．05）值并计算T0σ：对应T0（n，α）值表，当样本量n＝16、置信概率α为0．05时，对应的 T0值为2．44，故 T0σ＝2．44×0．2850＝0．6953。

（5）计算结果表明，16个检测值中14＃测量值的剩余误差为0．7255，大于T0σ（0．6953），根据格拉布斯准则应予以剔除。

（6）根据上述步骤继续对剩余15个数据进行检验，剔除0．303。

（7）根据上述步骤继续对剩余14个数据进行检验，剔除1．291。

（8）根据上述步骤继续对剩余13个数据进行检验，剔除0．640。

（9）根据上述步骤继续对剩余12个数据进行检验，无异常值检出。

根据格拉布斯准则共剔除4个异常值，分别为0．303、0．640、1．291、1．688。

2．4 狄克逊准则检验步骤及结果

（1）确定置信概率α为0．05。

（2）将 16 个数据从小到大依次排序：0．303、0．640、0．854……1．080、1．291、1．688。

（3）根据样本量选择极差比公式：该组数据样本量为16，属于14≤n≤30范围内，故选择公式分别对高端和低端异常值进行检验。

（4）计算Dn和D′n值，并确定较大值。

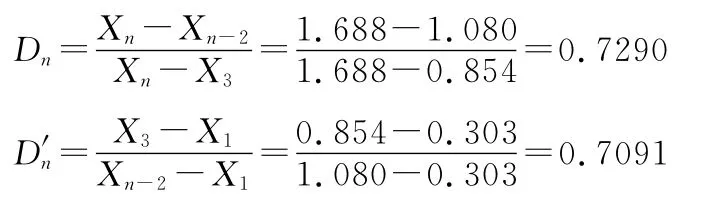
根据计算结果Dn＞D′n。

（5）查表获得D0．95值为0．547。

（6）根据狄克逊准则剔除异常值：由于Dn＞D0．95（16）故该组数据中最大值1．688应予剔除。

（7）根据上述步骤继续对剩余15个数据进行检验，剔除0．303。

（8）根据上述步骤继续对剩余14个数据进行检验，剔除1．291。

（9）根据上述步骤继续对剩余13个数据进行检验，剔除0．640。

（10）根据上述步骤继续对剩余12个数据进行检验，无异常值检出。

根据狄克逊准则共剔除4个异常值，分别为0．303、0．640、1．291、1．688。

2．5 罗马诺夫斯基准则检验步骤及结果

（1）确定置信概率α为0．05。

（2）将 16 个数据从小到 大依次排序：0．303、0．640、0．854……1．080、1．291、1．688。

（3）暂时去除X1后计算、σ′分别为1．0065、0．2321；｜X1－｜＝｜0．303－1．0065｜＝0．7035。

（4）经查表，当样本容量为16时，K 值为2．22，计算得到K（n，α）σ′值为0．5153。

（5）根据判定准则剔除异常值：由于｜X1－｜（0．7035）大于 K（n，α）σ′（0．5153），故判定0．303为异常值，予以剔除。

（6）根据上述步骤继续对剩余15个数据进行检验，剔除1．688。

（7）根据上述步骤继续对剩余14个数据进行检验，剔除1．291。

（8）根据上述步骤继续对剩余13个数据进行检验，剔除0．640。

（9）根据上述步骤继续对剩余12个数据进行检验，剔除1．080。

（10）根据上述步骤继续对剩余11个数据进行检验，无异常值检出。

根据罗马诺夫斯基准则共剔除5个异常值，分别为0．303、0．640、1．080、1．291、1．688。

2．6 讨论

以上判定准则都是以数据呈正态分布为前提，当数据偏离正态分布时检验结果不一定可靠。

从样本量的适用情况来看，拉依达准则不需查表，计算最为简便，但结果可靠性不高，尤其是在样本量较小时，因此拉依达准则通常用于样本量较大且对检验结果要求不太高时对大量检测数据进行初筛；样本量较小时选择狄克逊准则、罗马诺夫斯基准则对离群值的判定功效较优，肖维勒准则、格拉布斯准则检验样本量适中，但这一区分并不十分严格。细胞毒性试验多孔平行数据通常属于较小样本量，在实际运用中选择拉依达准则对其进行检验是不合适的。

从计算方式来看，肖维勒准则、格拉布斯准则、罗马诺夫斯基准则都需要计算标准偏差σ，并通过查表获得一个系数以此来计算相应临界值Xσ。对这三种准则分别对应的Zc值、T0值、K值表进行比较，罗马诺夫斯基准则最为严格，其次是肖维勒准则，格拉布斯准则相对较为宽泛［8］。除此之外，肖维勒准则所对应的Zc值大小只与样本量n相关，置信概率α对Zc值无影响，相较格拉布斯准则、罗马诺夫斯基准则以及狄克逊准则，肖维勒准则概率意义较为模糊。

从检出离群值的个数来看，以上5种判定准则均可以通过重复使用对可疑值进行逐一检出，但重复使用同一检验法可能犯判多为少的错误，重复检验时狄克逊准则较好，但计算相对复杂［4］。

3 结论

细胞毒性试验多孔平行数据属于小样本量数据，待检出的异常值不仅限于1个。根据细胞毒性试验多孔平行数据的特点综合考虑这5种准则的适用范围、计算方式、严格程度，选用狄克逊准则较为适宜，该准则概率意义明确，适用于对样本量较小的数据进行检验，且在需要对1个以上异常值进行检出时效果较好。值得注意的是，虽然可以通过重复利用狄克逊准则对数据中的多个异常值进行逐个检出，但在一组检出数据中，可疑数据应很少，若一组数据中的可疑数据较多，则提示数据测量体系可能异常，可考虑重新测量。

［1］林祥梅，王建峰，梅琳，等．用人角质细胞评价4种化妆品的细胞毒性［J］．毒理学杂志，2008，22（1）：75－76．

［2］夭建华，陈辉敏，方力，等．国内外卷烟危害性评价方法现状和发展趋势［J］．烟草科技，2007，（1）：50－53．

［3］苏建青，褚秀玲，李俊霞，等．中性红染色法检测人参皂苷及其衍生物对CEF增殖的影响［J］．安徽农业科学，2009，37（35）：17523－17525．

［4］GB／T 4883－2008，数据统计处理和解释 正态样本离群值的判断与处理［S］．

［5］马林茂．数据处理中异常值的取舍［J］．疾病监测，2010，（12）：992－993．

［6］乐立利．观测数据的异常值统计检验方法研究［D］．长沙：中南大学，2008．

［7］熊万杰，黄振中．用Origin软件处理物理实验数据［J］．大学物理实验，2004，17（2）：65－67．

［8］何平．剔除测量数据中异常值的若干方法［J］．航空计测技术，1995，（15）：19－22．