粒子群优化模糊聚类在信号分选中的应用

张中山，贾可新

（中国电子科技集团公司38所，合肥230088）

0 引 言

雷达辐射源信号分选是雷达对抗侦察系统的关键处理步骤，也是雷达对抗信息处理中的核心内容，其分选与识别水平是衡量雷达对抗侦察系统和信息处理技术先进程度的重要标志［1］。由于雷达信号分选事先无法获得训练样本，非监督分类方法特别是聚类方法倍受推崇，关于聚类在信号分选中的应用也是层出不穷。其中最为经典的有K均值聚类方法［2］、支持 矢 量 聚 类 （SVC）方 法［3］、模 糊 C 均 值（FCM）［4］聚类方法等。SVC方法由于需要大量的核函数的计算，所耗费的时间量和存储量较大。K均值方法由于属于硬划分方法，忽略了样本在性态和类属方面的中介性，割断样本之间的联系，使得所得到的聚类结果与实际要求偏差较大，并且极易陷入局部最优解。FCM是在K均值算法的基础上加入了模糊理论的思想，考虑了样本之间的联系，建立样本对于类别的不确定性描述，所得的聚类结果明显优于硬聚类方法，目前模糊聚类方法已成为聚类分析研究的主流。然而，基于梯度下降的FCM算法本质上是一种局部搜索算法，容易陷入局部极小值，得不到最优解，而且对初值敏感，即不同的初值可能会导致不同的聚类结果。

从自然界得到启发的粒子群优化（PSO）算法［5］，被认为是简单高效的一种全局优化算法，在通信、遥感等行业都有不少成功应用的例子。目前应用粒子群优化算法进行信号分选的方法不多，特别是结合FCM方法进行辐射源分类方法较为少见。本文利用了粒子群优化算法的全局寻优的优点，结合FCM的模糊理论，将其应用在雷达信号分选领域，不仅避免了梯度下降法所带来的容易陷入局部极小值的缺陷，同时也改善了不同初始聚类中心对聚类结果的影响，提高了雷达信号分选的正确度。

1 模糊C均值算法

模糊C均值聚类［6］的基本思想是通过求取所有样本点与聚类中心距离加权和作为目标函数，使得最小化目标函数，得到最终的聚类中心。FCM的目标函数可以表示如下：

式中：N为样本总数；c为聚类中心的数目；α为影响隶属度矩阵模糊度的加权指数，通常取为2；dik为样本x与聚类中心V之间的距离度量，通常使用欧氏距离。

FCM聚类可看作是对目标函数求极小值的问题，通过迭代调整，使得目标函数最小，其基本步骤如下：

（1）根据聚类数目c和权重m、算法终止误差精度ε，随机生成聚类中心矩阵V，令迭代次数l＝0；

（2）更新隶属度矩阵U；

（3）修正聚类中心V；

（4）若相邻2次的聚类中心矩阵V误差小于算法误差ε，则停止。

2 粒子群优化算法

粒子群优化算法是一种同时具有群体智能和进化计算优点的优化算法，和其他的进化算法相类似，它也是通过个体间的协作与竞争实现问题空间的最优化搜索。

PSO将n维搜索空间中每个无重量、无体积的备选解称为“粒子”，每个粒子将在解空间中以一定的位移和方向运动。通常粒子将追随当前的适应度最优的粒子而移动，并经迭代搜索最后得到最优解。在每一次迭代过程中，粒子将根据2个极值调整，一个是粒子自身经历的最优位置，称为个体极值pbest；另一个为整个粒子群经历的最优位置，称为全局极值pgbest。与此同时，每个粒子都有一个速度，记作v。粒子i根据以下公式［7］改变其位移方向和步长：

式中：w为惯性权值；d为总维度n维中的第d维；t为当前迭代次数；i＝1，2，…s，s为种群规模；Rand（）为分布于［0，1］之间的随机数；c1和c2为位移变换的限定因子或加速因子，通常取2。

x为当前粒子位置，粒子位移控制上限为vmax，如果某一维超过了设定的vmax，那么这一维的速度被限定为vmax。

其具体算法流程通常为［8］：

（1）初始化一群粒子（群体规模为m），包括随机位置和速度；

（2）计算每个粒子的适应度；

（5）根据式（2）调整粒子速度和位置；

（6）未达到结束条件则转（2）。

3 粒子群优化的模糊聚类算法

从FCM的原理可以看出，FCM可以归结为对目标函数求极值的问题。粒子群作为一种全局优化算法，对于解决这类问题具有很强的优势。使用粒子群优化算法进行模糊聚类的基本思路就是将聚类中心作为待求解的问题，将目标函数的相应形式作为适应度函数，当粒子群优化算法达到终止条件，最优粒子便是最佳聚类中心。

因此在粒子群优化模糊聚类中的3个关键问题是：粒子的组成、适应度函数的定义以及算法终止条件。首先，一个粒子代表着K个聚类中心，因此一个粒子可以用K×D的向量来表示，可采用实数编码方式，编码长度为K×D，结构为其中Cij第i个聚类中心在第j维的值。其次，适应度函数可以设为：

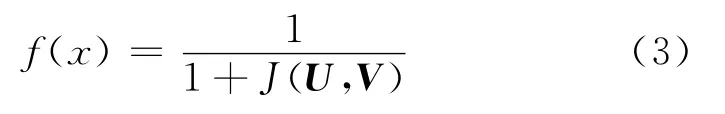
即J（U，V）越小，适应度值越高。最后，算法需要设定为满足以下条件之一后满足：

（1）当迭代次数大于或等于最大迭代次数；

（2）隶属度矩阵不变；

（3）适应度值前后变化小于误差值ε。

4 粒子群优化的模糊聚类算法在雷达信号分选中的应用

4.1 雷达信号特征分析

雷达信号分选是利用信号参数的相关性来实现的，表征雷达的特征参数有时域参数、频域参数、空域参数等［3］。通常用于信号分选的参数主要有5个：到达角、载频、到达时间、脉宽、脉冲幅度，这5个参数组合在一起，称为脉冲描述字。由于到达时间、脉冲幅度难以形成聚类相关性，因此对于聚类算法来说，较合理的参数是脉冲宽度、载频和到达角。

4.2 实验结果与分析

为了验证算法的有效性，本实验采用2组仿真数据进行实验。第1组样本信号产生的信噪比为10dB；第2组样本信号产生的信噪比为8dB。每组数据均有5个辐射源。每组仿真数据分别有10 000个脉冲数据，每部雷达包含2 000个脉冲数据，对于分选的评价指标为：

仿真环境为Matlab 7.0。FCM参数设计如下：类别数为5；最大迭代次数为100；模糊因子为2；误差值为1e＋5。PSO－FCM的参数：粒子个数为25；最大迭代次数为100；惯性权重为0.8；位移因子为2。将实验数据分别用FCM和PSO－FCM算法进行分选，实验结果如表1所示。

从实验结果可知，在数据集信噪比较高（数据集一）的条件下，PSO－FCM 分选正确率只是略高于FCM方法；而当数据集信噪比较低（数据集二）情况下，PSO－FCM的分选优势较为明显。

表1 不同信噪比条件下仿真数据的正确率

5 结束语

本文利用粒子群优化的模糊聚类对脉冲信号进行分选，仿真结果表明该方法优于传统模糊C均值方法。缺点在于使用粒子群优化的模糊聚类方法在带来正确率提升的同时，会造成计算时间的增加，如何减小算法时间和复杂度是下一步研究的目标。

［1］何明浩.雷达对抗信息处理［M］.北京：清华大学出版社，2010.

［2］张万军，樊甫华，谭营.聚类方法在雷达信号分选中的应用［J］.雷达科学与技术，2004，2（4）：219－223.

［3］国强.复杂环境下未知雷达辐射源信号分选的理论研究［D］.哈尔滨：哈尔滨工程大学，2007

［4］利稷夫.无监督聚类算法在辐射源信号分析中的应用［D］.成都：西南交通大学，2007.

［5］Kennedy J，Eberhart R.Swarm Intelligence［M］.San Francisco， CA： Morgan Kaufmann Publishers，Inc.，2001.

［6］Ruspini E H.New experimental results in fuzzy clustering［J］.Information Science，1973，18（2）：273－287.

［7］Eberhart R C，Shi Y.Tracking and optimizing dynamic systems with particle swarms［A］.Proc.IEEE International Congress on Evolutionary Computation（CEC 2001）［C］，2001：94－97.

［8］谢晓锋，张文俊，杨之廉.微粒群算法综述［J］.控制与决策，2003，18（2）：129－134.