反射式椭圆高斯光束平顶整形系统

孟祥翔，刘伟奇，柳 华，魏忠伦，康玉思，冯 睿，吕伟振

(1.中国科学院长春光学精密机械与物理研究所，吉林长春 130033; 2.中国科学院大学，北京 100049)

1 引 言

激光自问世以来得到了广泛的应用。在光刻[1]、激光医疗[2]、材料加工[3-6]、全息[7]等技术领域，往往需要光强分布为平顶函数的圆形或方形激光光束。现在对激光光束平顶化整形主要有采用二元光学元件[8]、液晶空间光调制器[9]、双折射透镜[10]、基于几何光学方法设计的折射(或反射式)透镜[11-15]等方法。采用几何光学方法设计的激光光束平顶系统因其具有高能量利用率和适用于高功率激光等优势得到了广泛的应用。目前，采用几何光学方法设计的折射式激光光束整形器[11-13]已发展成熟。为整形效果不受入射光波长影响且适用于高功率激光，Malyak[14]首先提出了无中心遮拦的反射式高斯光束整形系统。部分准分子激光光束[15]和使用单片非球面准直的半导体激光光束均可近似为椭圆高斯光束，在准分子激光医疗等领域往往需要光斑形状为圆形的激光光束，所以必须对椭圆高斯光束进行平顶化整形。Vladimir Oliker[16]在对两镜光束整形系统的研究中提出了一组二阶非线性偏微分方程描述反射镜面形，其优点是不受入射光束和出射光束对称性的影响，在入射面和出射面坐标关系确定的情况下，可以将任意分布的准直入射光束整形为所需分布的准直出射光束，但是对于二阶非线性偏微分方程组的数值求解和编程比较困难。

本文介绍了将椭圆高斯光束转化为圆形平顶光束的无中心遮拦反射式两镜整形系统的设计方法，给出了两反射镜积分形式的面形方程，简化了设计步骤，并针对美国GAM LASER公司的EX5/250 ArF准分子激光器设计了整形系统，分析了系统参数对整形效果的影响。

2 理论分析

采用几何光学方法设计激光光束平顶整形器的主要依据是能量守恒、折/反射定律、等光程条件[12]。利用能量守恒推导出入射面坐标和出射面坐标的对应关系;然后利用标量或矢量形式的折/反射定律进行光线追迹，代入等光程条件，即可求出整形系统的面形方程[15]。

2.1 坐标关系

图1(a)为反射式椭圆高斯光束整形器在y-z平面的原理示意图，假设入射光束和出射光束都平行于光轴，输入光束和输出光束在x-y平面上的剖面图如图1(b)所示，定义(r，θ)为入射面的极坐标，(ρ，φ)为出射面的极坐标。

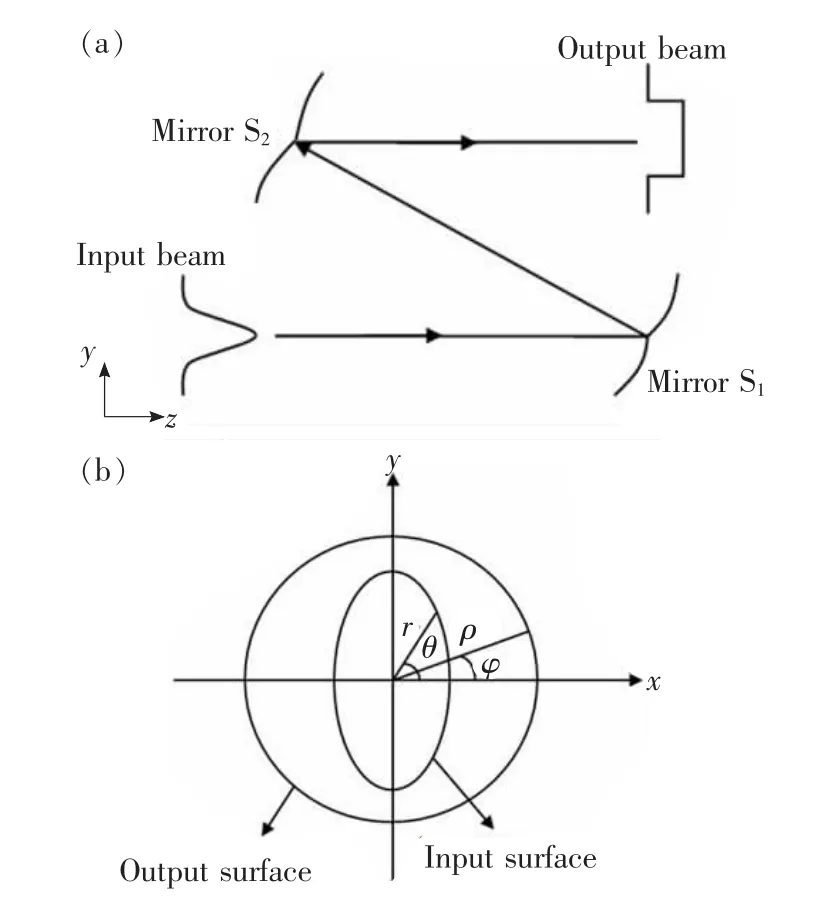
图1 反射式激光光束整形系统示意图。Fig.1 Scheme reflective laser beam shaping system.

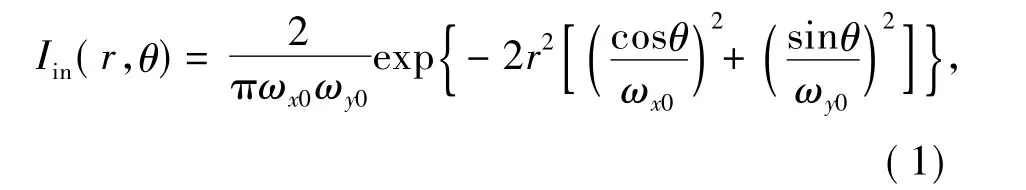
设入射椭圆高斯光束光强分布方程为其中ωx0和ωy0分别为椭圆高斯光束x和y方向上的束腰，定义 ωy0/ωx0=m。

为方便积分，采用匀化洛伦兹函数作为出射光强分布:

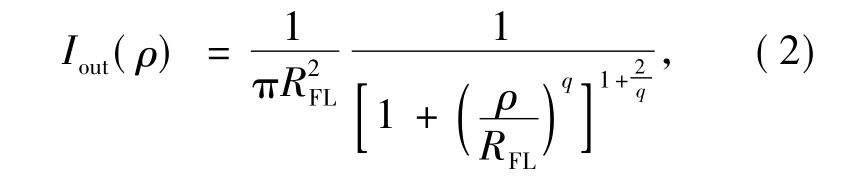
式中RFL为出射平顶光强分布的半高宽。q决定着匀化洛伦兹函数的形状，选择合适的q值，即可得到目标出射平顶分布。

针对椭圆高斯光束这种非旋转对称形式的光束轮廓，根据能量守恒定律要求有

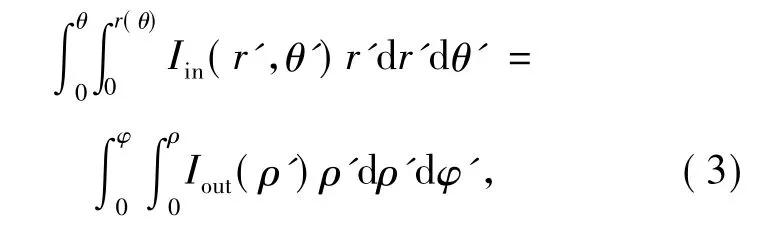
椭圆方程的极坐标形式为

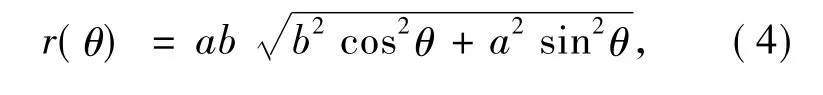
其中a、b分别为椭圆的短轴半径和长轴半径。为便于之后的运算选择积分路径，设a=r0，b/a=n，则b=nr0。当n取定值时，椭圆方程可化为

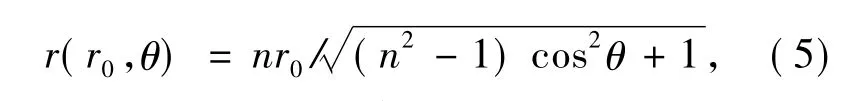
令n=m，则入射椭圆光束光强分布可化简为

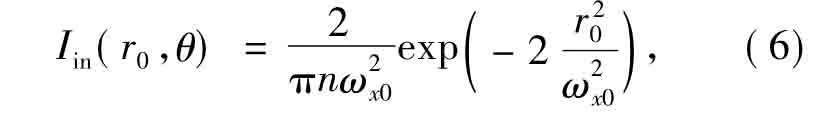
将式(2)、(5)、(6)代入式(3)，可得:

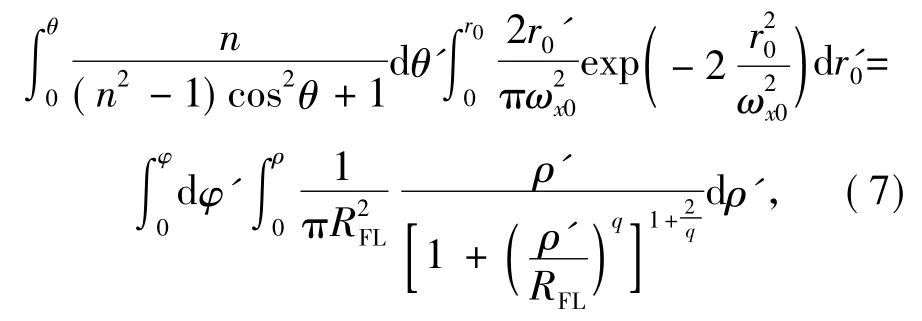
分离变量可求得(r0，θ)与(ρ，φ)的坐标关系为

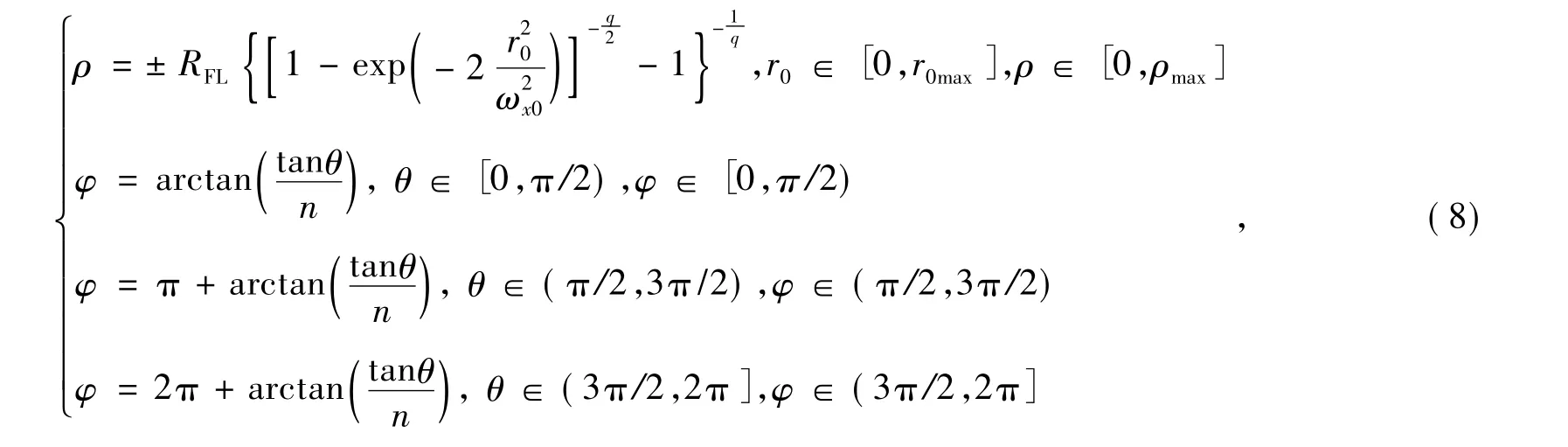
当θ=π/2时，φ=π/2;当 θ=3π/2时，φ=3π/2。其中ρ与r0的关系中取正号代表系统无实焦点，取负号代表系统有实焦点。当n值一定时，r0的大小就确定了一个椭圆，(r0，θ)则能唯一确定椭圆圆周上的一个点且r0与θ无关。此时即可将入射面看作无数个几何中心相同，长轴与短轴之比一定的椭圆的集合，每个椭圆在经过系统变换后与出射面上的一个圆对应，这样就实现了光束形状由椭圆到圆的变换。

2.2 面形方程

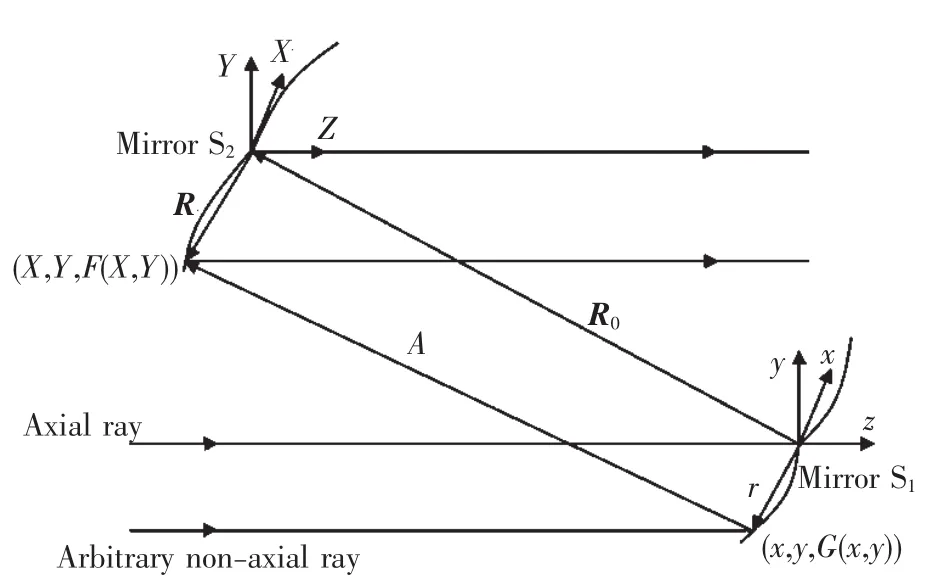
图2 反射镜面形计算原理图Fig.2 Principle of calculating reflective surfaces

反射式激光光束整形系统的面形方程推导过程与折射式整形系统[8]相似，区别仅在于采用矢量形式的反射定律进行光线追迹[14-15]。图2为反射式光束整形系统面形计算原理图，反射镜S1和反射镜S2的面形分别在局部坐标系(x，y，z)和(X，Y，Z)中描述，两局部坐标系均以对应反射镜的轴上中心为原点，面形方程分别为z=G(x，y)和 Z=F(X，Y);设局部坐标系(X，Y，Z)的原点在局部坐标系(x，y，z)中的坐标为(X0，Y0，Z0)，因此轴上光线从反射镜S1中心反射到反射镜S2中心的矢量R0=(X0，Y0，Z0);任意轴外光线在反射镜 S1上的入射点为(x，y，G(x，y))，反射光线单位矢量为A，在反射镜S2上的入射点为(X，Y，F(X，Y))。

因为假设入射光线和出射光线均平行于光轴，为确保输入输出波前均为平面波，引入等光程条件[15]，即轴上光线在输入输出面之间经过的光程等于任意轴外光线在输入输出面之间经过的光程。根据等光程条件可以推得:2

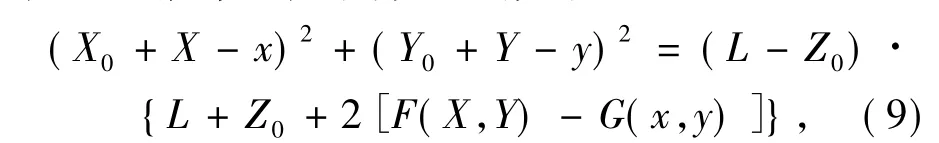
利用矢量形式的反射定律[15]并代入等光程条件可以得到G(x，y)对x和y的偏导Gx'和 G'y为:

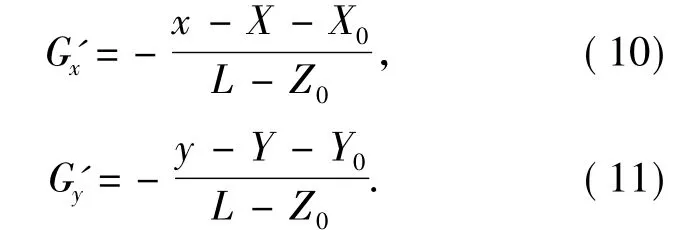
由于已将入射面椭圆方程转化为r0和θ的函数，因此，需求出以r0和θ为自变量的反射镜S1的面形方程G(r0，θ)。设两反射镜的中心在同一y-z平面内，则 X0=0。根据 x=rcosθ，y=rsinθ，X= ρcosφ，Y= ρsinφ 可求出 G(r，θ)对 r和θ的偏导，联立式(5)可求出 G(r0，θ)对 r0和 θ的偏导为

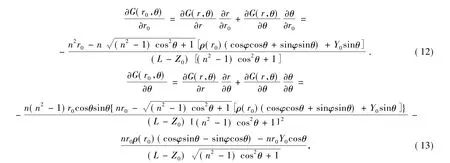
最后通过积分可求得G(r0，θ)为

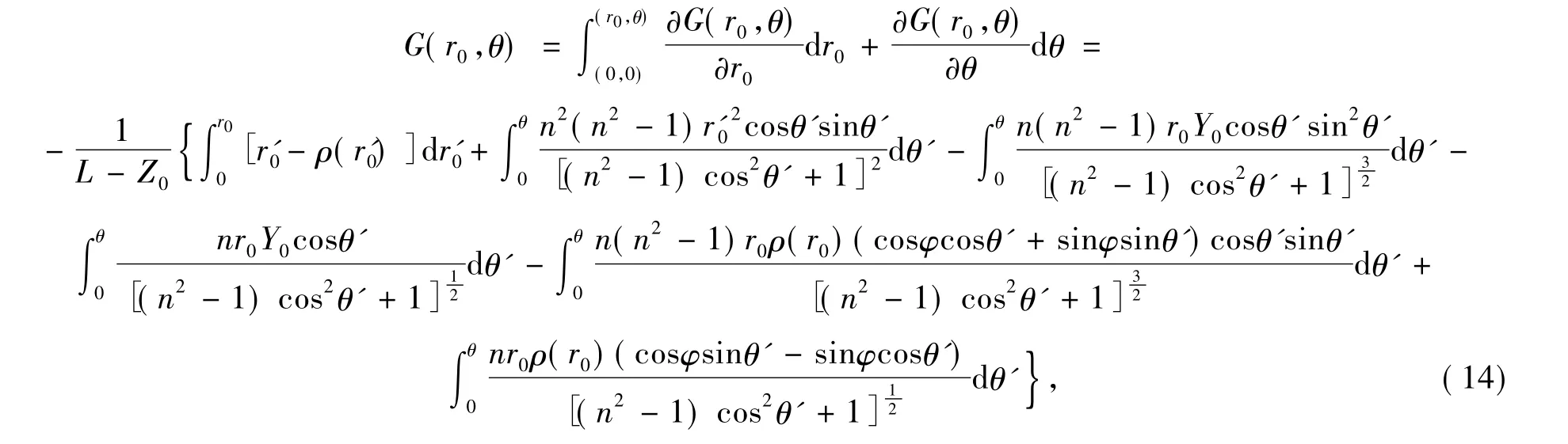
通过式(12)可推出 F(ρ，φ)和 G(r0，θ)的关系式为

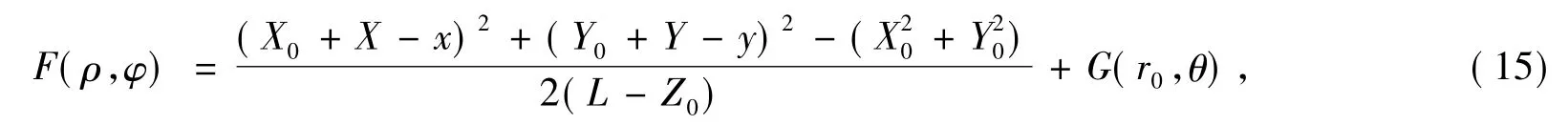
将 x=rcosθ，y=rsinθ，X=ρcosφ，Y=ρsinφ 以及式(5)代入上式可得

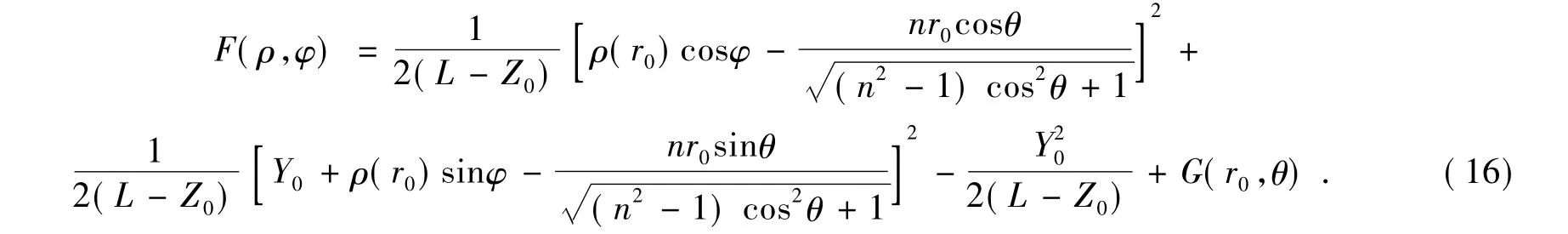
所求得的面形方程为积分形式，在MATLAB等数值计算软件中有自带函数可以调用，相比起二阶非线性偏微分方程组，简化了数值计算步骤。在求解时，首先给定入射光束各点坐标值(r0，θ)，通过坐标关系式(8)，利用 MATLAB软件求出入射光束各点在出射面对应点的坐标值(ρ，φ)的数值解，然后一起代入式(14)、(16)求出两面形方程的数值解。以上推导的坐标关系式(8)和反射镜面形方程 (14)、(16)亦适用于对圆形高斯光束平顶整形，此时只需取m=n=1即可。

3 数值仿真

以美国GAM LASER公司的EX5/250 ArF准分子激光器为例，设计与其适用的反射式椭圆高斯光束整形器。EX5/250 ArF准分子激光器在水平方向上的光束尺寸为3 mm，束腰半径ωx0=0.75 mm，FWHMx为 1 mrad;在竖直方向上的光束尺寸为6 mm，束腰半径ωy0=1.5 mm，FWHMy为2 mrad，可取m=n=2;对以匀化洛伦兹函数表示的出射平顶光束，取RFL=3 mm，q=50。反射镜S2相对于反射镜S1的位置坐标(X0，Y0，Z0)=(0，10，－20)，长度单位为 mm。

利用MATLAB软件采用数值解法求解面形方程，首先求解第一面反射镜面形数据，在x-y面上选择包含入射光束最大椭圆边界的矩形区域，并对矩形区域进行离散，离散间隔分别为xi和yi，离散点为(xn，yn)，这些点对应的矢高值便是要求的第一面反射镜的面形数据。然后，求出离散点(xn，yn)对应的极坐标形式(rn，θn)，再利用式(5)求出与(rn，θn)对应的(r0n，θn)，此时 x-y 面各点已化为(r0n，θn)的形式以代表各条光束入射点。利用式(8)求出出射面上与(r0n，θn)对应的坐标(ρn，φn)，并将(r0n，θn)和(ρn，φn)代入式(14)，使用MATLAB中自带的积分函数quadl函数计算出矢高值 G(r0n，θn)。

使用光学软件ZEMAX进行模拟，选择grid sag面形，基准面为平面，使用线性插值。由于grid sag面形格式要求对输入的面进行单独离散，在计算第二面反射镜面形数据时，需重新编程对出射面进行离散，离散点为(Xn，Yn)，求出其对应的极坐标形式(ρn，φn)，再根据式(8)计算出入射面对应的坐标(r0n，θn)。之后的运算与计算第一面反射镜面形数据时相同，计算出G(r0n，θn)，最后再利用式(15)求解出 F(ρn，φn)。

第2节的理论分析是以入射光束发散角为0°为前提，为了增加仿真的精确性，在数值计算时计算入射光束发散角为0°时的面形数据，然后在光学软件中加入角度进行仿真。可得到整形系统如图3所示，光线追迹结果如图4所示。可以看出较小的入射光束发散角对该系统的整形效果基本没有影响。

选取光束出射方向上距离反射镜S220 mm处作为目标面，以下式定义目标面照度均匀性P为

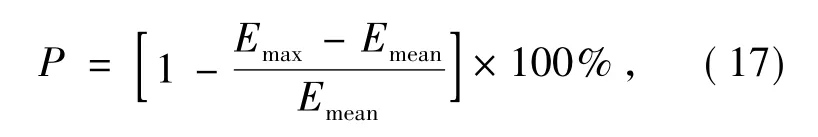
其中Emax为目标区域内的最大照度值，Emean为目标区域内的平均照度值。取半径为2.84 mm的圆域作为目标区域，计算得到在目标区域内照度均匀性为95.45%;利用式(2)和式(17)，可求得理想出射光束在目标区域内的均匀性为99.86%;实际值与理想值之间的差别主要由于加入发散角追迹光线和光学软件对于离散面形数据的插值误差而引起的。

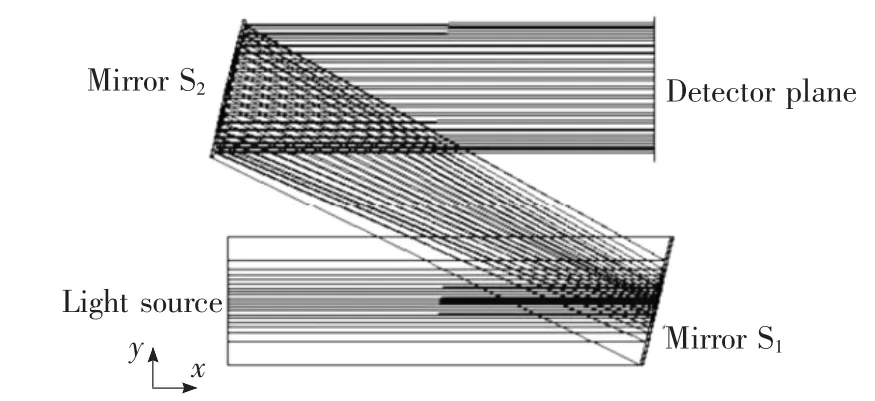
图3 反射式椭圆高斯光束整形系统y-z平面的光线追迹图Fig.3 Ray trace in y-z plane of the reflective elliptical Gaussian beam shaping system

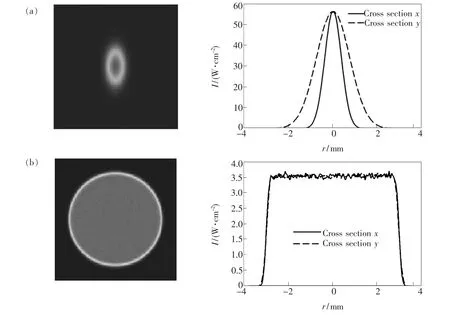
图4 ZEMAX非序列光线追迹结果。Fig.4 Results of non-sequential ray tracing in ZEMAX.

4 系统分析

假设过S1中心的切平面为u-v平面，以该面为基准面分析反射镜S1的面形随参数Y0和Z0的变化规律。首先固定 Z0=20 mm，改变 Y0，反射镜S1在正交方向上的轮廓曲线S1(u，0)和S1(0，v)的变化如图5(a)所示;固定Y0=10 mm，改变Z0，反射镜 S1在正交方向上的轮廓曲线S1(u，0)和 S1(0，v)的变化如图 5(b)所示;等比例增大Y0和Z0，反射镜S1在正交方向上的轮廓曲线S1(u，0)和S1(0，v)的变化如图5(c)所示。

综合图5(a)、(b)、(c)可知，单独增加 Z0和等比例增加Y0、Z0时，反射镜S1在u和v方向上面形斜率同时变缓，可在一定程度上降低加工难度，且S1在u方向上的面形深度要比在v方向上的面形深度大一个数量级。用同样的方法分析反射镜S2，发现S2的面形随参数Y0和Z0的变化规律与反射镜S1相同。此外可以看出设计的反射镜面形为非回转对称曲面，相比传统回转对称的球面镜和非球面镜增加了加工难度。以超精密单点金刚石车削技术、流体辅助光学加工等为代表的先进光学制造技术发展迅速，使得加工高精度非回转对称光学曲面成为现实，目前采用飞刀铣削、快刀伺服车削和慢刀伺服车削技术均能加工复杂光学曲面。本文设计的非回转对称反射镜关于横、纵坐标轴对称，在一定程度上降低了加工检测难度。

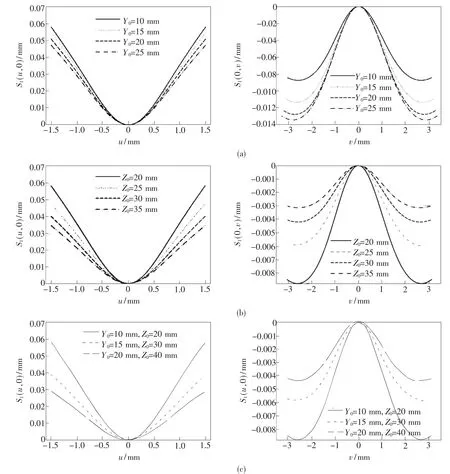
图5 反射镜S1正交方向剖面轮廓与Y0、Z0关系图。Fig.5 Relationships between surface profile of S1in cross section and Y0，Z0.

固定的椭圆高斯光束平顶整形器只针对特定的束腰大小使用，当束腰大小改变时，出射光束的平顶性也随之改变。保持n=2，改变椭圆高斯光束在快慢轴上的束腰大小，出射光束光强轮廓如图6所示。当入射光束束腰偏差在±0.05 mm时，出射光束均匀性降低到83%;当入射光束束腰偏差在±0.1 mm时，对出射光束平顶性的影响已经非常严重。因此，在使用椭圆高斯光束平顶整形器时，应确保入射光束束腰大小与整形器相匹配。

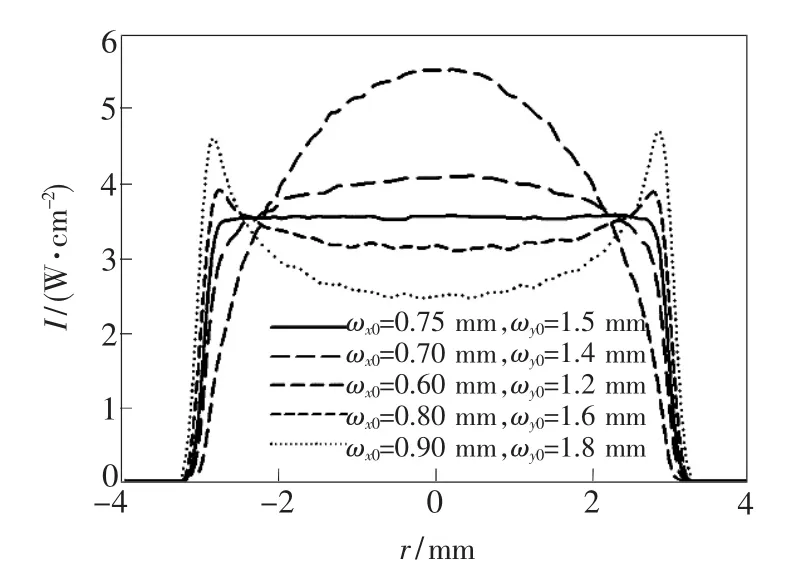
图6 出射光束平顶性与入射光束束腰偏差关系图Fig.6 Relationship between the uniformity and the incident beam waist deviation

反射镜的面形误差直接影响着系统的整形结果。分析系统面形误差时，我们对通过式(8)、(14)、(16)计算出的有限个点的数值解加入正态分布的误差值[17]，利用ZEMAX非序列进行几何光线追迹，分析系统面形误差对整形效果的影响。图7为引入的均方根误差值对光束出射方向上距离反射镜S220 mm处的目标面上辐照度均匀性的影响。由图可知，目标面上的辐照度均匀性在均方根误差值不大于1 μm时在95%左右，当均方根误差值大于1 μm时，辐照度均匀性快速降低。考虑到反射式整形系统更适合用于高功率激光器，为提高反射镜表面抗激光损伤阈值，反射镜的面形加工误差应该更低。

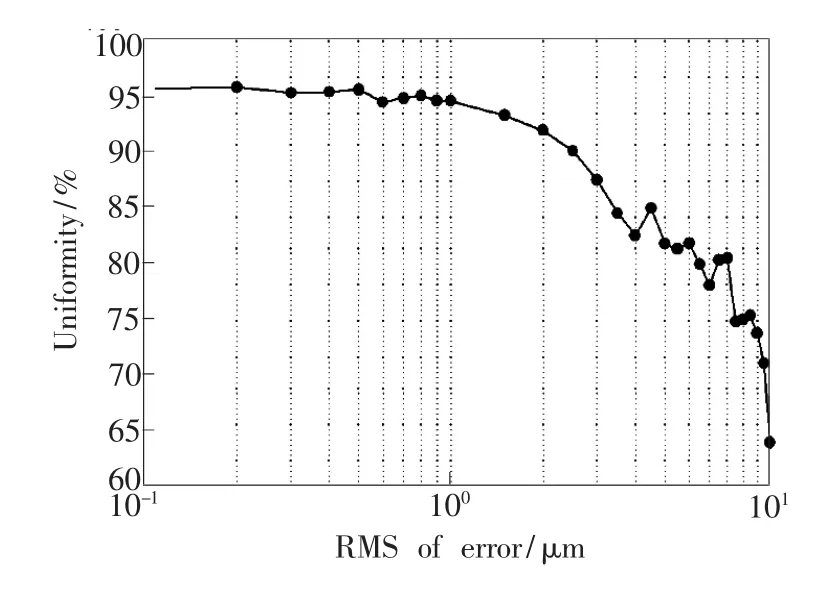
图7 出射光束均匀性与面形均方根误差关系图。Fig.7 Relationship between the uniformity and the RMS of surface error

5 结 论

提出了一种将椭圆高斯光束转化为圆形平顶光束的整形方法。为了同时适用于各波段和高功率情况，采用了无中心遮拦反射式结构，利用能量守恒和矢量形式的反射定律推导了同时适用于椭圆高斯光束和圆形高斯光束整形的坐标关系和面形方程，并给出了设计实例。从面形加工难度和输出光束平顶性两方面对系统进行了分析，认为增加两反射镜的水平距离和等比例增加水平和竖直距离有利于降低反射镜的加工难度。该整形系统对入射光束尺寸要求严格，但对于面形加工精度要求较低。

[1]Zhao Y，Gong Y.Design of beam shaping unit for deep ultraviolet lithographic illumination system[J].Opt.Precision Eng.(光学 精密工程)，2011，19(1):29-34(in Chinese).

[2]Liu H，Liu B Y，Bai Y L，et al.Design of arbitrary waveform generator for shaping high power laser system[J].Chinese Optics(中国光学)，2011，4(1):60-65(in Chinese).

[3]Zhang Z J，Liu Y，Miao G Q，et al.The 2 kW semiconductor laser processing light[J].Chin.J.Lumin.(发光学报)，2013，34(3):334-339(in Chinese).

[4]Wang P C，Deng Y L，Zhang L P，et al.High brightness fiber coupled diode laser module[J].Chin.J.Lumin.(发光学报)，2012，33(12):1335-1341(in Chinese).

[5]Hao M M，Zhu H B，Qin L，et al.Research on high brightness fiber coupled diode laser module with hundred watts class output power[J].Chin.J.Lumin.(发光学报)，2012，33(6):651-659(in Chinese).

[6]Xie J J，Gao F，Pan Q K，et al.Laser mask micromachining system based on beam-scanning widening techningue[J].Chin.Opt.(中国光学)，2011，4(6):654-659(in Chinese).

[7]Ma J S，Xia F P，Su P，et al.Survey on key techniques and systems of digital holographic 3D display[J].Opt.Precision Eng.(光学 精密工程)，2012，20(5):1141-1152(in Chinese).

[8]Chang Y H，Ishii Y，Murata K.Reshaping collimated laser beams with Gaussian profile to uniform profile[J].Appl.Opt.，1983，22(22):3644-3647.

[9]Yu X C，Hu J S，Wang L B，et al.Laser beam shaping based on liquid-crystal spatial light modulator[J].Acta Optica Sinica(光学学报)，2012，32(5):0514001-1-5(in Chinese).

[10]Yang X T，Fan W.Spatial laser beam shaping using birefringent lenses[J].Acta Optica Sinica(光学学报)，2006，26(11):1698-1704(in Chinese).

[11]Frieden B R.Lossless conversion of a plane laser wave to a plane wave of uniform irradiance[J].Appl.Opt.，1965，4(11):1400-1403.

[12]Hoffnagle J A，Jefferson C M.Design and performance of a refractive optical system that converts Gaussian to a flattop beam [J].Appl.Opt.，2000，39(30):5488-5499.

[13]Zhang S，Neil G，Shinn M.Single-element laser beam shaper for uniform flat-top profiles[J].Opt.Exp.，2003，11(16):1942-1948.

[14]Malyak P W.Two-mirror unobscured optical system for reshaping the irradiance distribution of a laser beam[J].Appl.Opt.，1992，31(22):4377-4383.

[15]Shealy D L，Chao S H.Geometric optics-based design of laser beam shapers[J].Opt.Eng.，2003，42(11):3123-3138.

[16]Oliker V.Optical design of freeform two-mirror beam-shaping systems[J].J.Opt.Soc.Am.A，2007，24(12):3741-3752.

[17]Shang J L，Zhu X，Chen P，et al.Refractive optical reshaper that converts a laser Gaussian beam to a flat-top beam[J].Chin.J.Lasers(中国激光)，2010，37(10):2543-2549(in Chinese).