关于专科词典释文“专业”与“通俗”的思考

陈为众

(上海辞书出版社 上海 200040)

本文就专科词典释文“专业”与“通俗”之间的相互关系提出笔者个人的观点和见解，求教于方家。

徐庆凯的新著《专科词典论》(2011)对专科词典的特征做了如下概括:

似可将专科词典的特征概括为一个字:专。读者对象主要是相关知识领域的专业工作者，也包括对该专业懂得较多、兴趣较大的人;选题是从专业的角度定的;词目是从特定专业的范围内选的;释文主要是从特定专业的角度写的，目的是给读者提供丰富的专业知识(丰富的程度因词典规模的不同而不同)，作为解惑释疑、增长知识、查找线索的参考。

如上所述，确定读者对象是编纂专科词典的出发点和立足点，词目是脸面，释文是内涵。虽说专科词典的读者对象主要是相关知识领域的专业工作者，也包括对该专业懂得较多、兴趣较大的人，同时也不能排除对该专业懂得不多而兴趣较大、需要深入了解的读者。因此，能够用通俗的语言来表达深奥的内涵是专科词典编纂者的目标之一。对于自然科学、技术科学类的专科词典而言，编纂者还承担着普及科技知识的任务，因此必须考虑专科词典潜在读者的需要和特点。

对于语文词典来说，用词最好是自封闭的，即在词典的释文中所使用的词最好都收录在该词典中。这一点，《朗文当代高级英语辞典》(Longman Dictionary of Contemporary English)就做得比较好。它是一部语文性辞书，书末附有一个约2000单词的词汇表，全书的释义和例句所用到的词汇都限定在该词汇表的范围内，少量超出该范围的释义用词排成特殊字体。这就给使用该词典的读者提供了一个基本的保证，即尽量不使用读者不了解的单词来解释一个需要了解的单词。

对于专科词典而言，不承担提供字或词的语文性释义(如读音、词形等)的功能，而只对字或词在该学科中的特定涵义做百科性或专科性的释义。如在一部介绍度量衡单位的词典中收录作为长度单位的“米”、作为质量单位的“克”，在该词典的释文中是不会也不应该出现这些词汇的语文性释义的。所以专科词典不可能实现对所有参与释义的字词有封闭性，但对学科基本词汇和术语，还是需要这种收词上的封闭性的，特别是在有些释文不得不使用专业术语的情况下更应做如此规定。

作为一部承担科学普及功能的专科词典，在起点上可以降低使用者的基础背景知识，即使用浅显通俗的语言来表达高深的科学原理。这是应该做到，也是可以做到的。

在20世纪30年代曾经有过这样一首打油诗:

深入浅出是通俗，浅入浅出叫庸俗，深入深出犹可为，浅入深出最可恶。

这首打油诗虽然是针对语言文字的风格，但其意义远远超过文风问题，对世道人心、为学做人都大有启发。把它用在对专科词典的编纂上也是有指导意义的。

对于一部为专业工作者编写的专科词典来说，深入深出似乎是天经地义、顺理成章的事。可以说，大凡学术类的著作，很多都是这样写的。科学成果的表达方法，特别是像数学、物理学、天文学等的有些内容，可能难以做到生动通俗，但是使用符号语言系统还是文字语言系统是可以有差别的。使用符号语言系统简洁明了，但读者必须熟悉这种符号语言系统才行，否则就如同看天书一般。

虽说专科词典是给该专业领域内的专业工作者使用的词典，但还是需要为普及科学知识做努力的，专科词典也可以看作是一种高级的普及科学知识的材料。因此在对专科词典的词条进行释义时应当尽可能地用通俗简洁的文字来表达专深的科学内涵。

下面简要介绍几种一般专科词典的释义方法。

1．用一个通用术语来解释另一个专业术语

用一个专业术语来解释另一个专业术语，对专业工作者而言，层次、概念都比较清晰，语言也比较简练。若用浅近的文字、通用的术语来解释一个专业术语，可能要用较多的文字，但却能够使更多的读者看得懂、能够理解，受众面会更加广泛，对读者而言是有利的。

如有一部专科词典中有这样一个条目“视星等”。其释义如下:

是天体真亮度、天体到观测者的距离，以及在这一距离中星际物质吸收量的函数。

这里，使用了一个数学专业术语——函数。函数表示每个输入值与唯一输出值的一种对应关系。通俗地说，函数就是两个(或多个)值之间存在的一种对应关系，其中一个值的改变，会引起另一个值相应地改变。

而在同一部词典中另有一个条目“黑障区”。其释义如下:

区段范围与宇宙飞行器的外形、材料、速度，以及发射信号的频率和功率有关。

该释义用一个“与……有关”的普通词语就把它们之间存在的对应关系这一概念表达清楚了，比较通俗。因此，仿照此例，对于“视星等”的释义，可用通俗的语言表达为:与天体真亮度、天体到观测者的距离，以及在这一距离中星际物质的吸收量有关。

辞典的释文所要表达的是一个概念，辞典不是操作手册，也不是专业的教科书，更不是专著，有些表述不一定要定量，只要定性就可以了。前文所举的两个条目，表示定性关系的释文前一个专业，后一个通俗。用专业术语表达的定义虽然科学，符合事物本身的属性，但太抽象，不直观，并需要有专业知识，有时似无此必要。

有时用普通的词语不能取代专业术语，那还是应该使用专业术语来描述。如有一部词典中有一个条目“君子兰”，其释义如下:

多年生草本植物，根肉质，叶子宽带形……

曾有读者针对该释义中的“带形”提出意见，认为“带形”宜改为“条形”，其理由也就是为了统一，因为该词典中叶子用“带形”描述的语词仅此一条而已，而其他的如“银杉”“远志”条中关于叶子形态描述的语词都用“条形”。其实不然，查《中国高等植物图鉴》中“植物分类学上的常用术语解释”对叶子形状的描述可以发现，条形(线形)——长而狭，长约为宽的五倍以上，且全长略等宽，两侧边缘近平行;带形——宽阔而特别长的条形叶。因此无论用其他什么语词来描述该叶子的形态都很难准确、完整、简洁地表达，只能用“带形”这一专业术语来描述。同时，作为辞书封闭性的要求，需要把“带形”这一专业术语作为词目收录到该词典中。如果漏收该词目，就是不完整的，就没有达到通俗性的要求。

2．用文字叙述代替专业的数学符号和公式

在自然科学或工程技术类的专科词典中，用数学公式来表达不同量、值、单位之间的关系是很常见的。这对需要定量化的表达要求来说，是能够以最简洁的方式表达关系的。但这涉及两个因素:第一，编纂者和读者必须使用同一种符号系统，而且读者能够完全理解编纂者所使用的符号系统。第二，确有使用这种符号系统的必要性。如果不要求释文表达某种具体的关系，就不必使用符号系统，用简单的文字表述就可以了。

如有一部词典在释义“资产风险”时用了如下公式:

R=V×［ΣCRti×Qc+ΣARti×Qa+ΣIRti×Qi］，其中，R为该资产的总体风险值;V为该资产的量化评分;Rti为该资产第i个威胁的风险系数;CRti，ARti，IRti分别为第i个资产威胁列表中与机密性、可用性、完整性相关的威胁特性系数;Qc、Qa、Qi分别为该资产与机密性、可用性、完整性相关的信息安全特性系数。

虽然列出了公式，但对于不熟悉数学符号的读者来说几乎无用，因为这些符号所代表的数值对于具体的内容而言都是特定的，一般仅列出公式而不确定这些系数是无法仿照此计算的。实际上，只需指出“资产风险”的定义，并指出其与哪些因素有关即可。从一般的抽象概念上与机密性、可用性、完整性相关。就具体的实际问题而言，有其特定的风险因子和系数，如财务公司的资产风险主要有流动性差、信贷集中率高、资产致死率高、效益回报率低等。

即使同样是使用数学符号和公式，也还存在不同层次的问题。

如在一部专科词典中有“胡克定律”这一条目，其中的公式是写成分量形式的广义胡克定律。其释文如下:

材料力学和弹性力学的基本定律之一。各向同性物体受力时，如其应力在弹性极限范围内，则应力与应变成正比关系，其比值称“弹性模量”。将其推广到复杂应力(三维)状态，称为“广义胡克定律”，可表达为:

式中，ε为正应变，σ为正应力，γ为剪应变，τ为剪应力，E为弹性模量，G为剪切弹性模量，υ为泊松比。

上述释文中的公式也可写成张量形式的，如下所示:

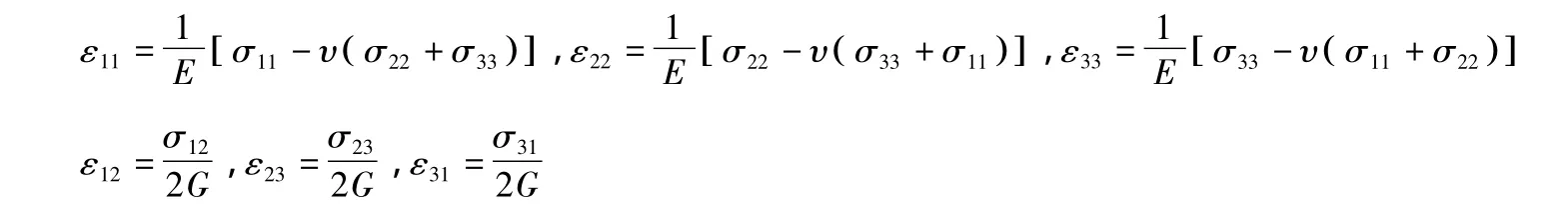
这里，由于采用了不同的符号系统和表达形式，其符号及系数都有所不同。虽然ε仍为应变的符号，σ仍为应力的符号，但取消了表示剪应变的γ和表示剪应力的τ，改用不同的下角标表示，当两个下角标相同时表示的为正应力或正应变，当两个下角标不相同时表示的为剪应力或剪应变。因此上述6个方程可以写成一个统一的矩阵形式。即:σij=Eijklεkl。这个公式看上去比较简洁漂亮，但要涉及张量知识。对于不了解张量知识的读者来说，可能会误以为用错了符号和系数。

3．是用结论性描述还是用过程性描述

专科词典的释义应当是一个直接的结果而不是一个过程性描述。

先看以下两个条目:

声学测温 利用声学原理测量气温的一种方法。即在仪器沿风向一固定距离d(约0．5米)的两端，各置放一对发声器和接收器，分别发送和接收顺风和逆风声音。发送器和接收器均安置在随风转动的风向标上，使之始终处于顺风和逆风位置。为避免受环境噪声的干扰，可采用100～200千赫兹的超声脉冲，每秒发射300次。因顺风和逆风通过距离d的时间分别为t1［=d/(c+v)］和t2［=d/(c－v)］，式中c为声速，v为风速，故t1+t2≈2d/c。再考虑绝对气温T与声速c的关系，对干空气言即可计算出绝对气温如使仪器的计算部件具有上述计算功能，则此仪器即成为“声学测风测温仪”。

声学测风 利用声学原理测量风速的一种方法。即在仪器沿风向的一固定距离d(约0．5米)的两端，各置放一对发声器和接收器，分别发送和接收顺风和逆风声音。设c为声速，v为风速，测量顺风声音从接收到发声的时间公式为t1［=d/(c+v)］，逆风声音从接收到发声的时间为t2［=d/(c－v)］。由两式可知风速为便于取顺风声音和逆风声音通过距离d的时间t1和t2，发声器和接受器均安设在随风转动的风向标上，使之始终处于顺风和逆风位置。为避免受环境噪声干扰，可采用100～200千赫兹的超声脉冲，每秒发射300次。又在设备中加入计算上式风速值的计算系统，即可得风速值。上述声学测风设备，实际上是一种自动测量风向和风速的声学测风仪。

首先，这两条释文写得有点过于专业，或者说有点复杂，主要是用了过程性的释义，并且颠倒了因果关系。依释文所描述，气温或风速是未知量(或待求的量值)，是需要根据实际测量的顺风声音从接收到发声的时间t1，逆风声音从接收到发声的时间t2计算出来的。其实，不需要像一般教科书里那样的推导过程，因此上述的t1和t2后括号内夹注的公式是不必要的。其次，这两条释文混淆了辞书和数学上的表达习惯。上述的t1和t2后括号内的这种表达形式是辞典中常用的夹注形式，但这不符合数学的表达习惯，容易引起不必要的误解。这两条一前一后，但采用了不同的处理方法。在“声学测风”条中的“由两式可知风速v”后直接跟一个等号引出的公式，而在“声学测温”条中的“即可计算出绝对气温T”后却用了一个夹注形式引出一个公式。按照用结论性描述的原则试改写前一条释文如下:

声学测温 利用声学原理测量气温的一种方法。即在仪器沿风向一固定距离d(约0．5米)的两端，各置放一对发声器和接收器，分别发送和接收顺风和逆风声音。发送器和接收器均安置在随风转动的风向标上，使之始终处于顺风和逆风位置。为避免受环境噪声的干扰，可采用100～200千赫兹的超声脉冲，每秒发射300次。分别测定顺风和逆风通过距离d的时间t1和t2，即可计算出绝对气温T。再考虑绝对气温T与声速c的关系予以修正。如使仪器的计算部件具有上述计算功能，则此仪器即成为“声学测风测温仪”。

4．用直接表示法取代间接表示法

词典的释文要言简意赅、直截了当，而不宜拐弯抹角地用间接的方式表达意思。如以下三条定义:

极圈 地球上距南北极各23°26'的纬度圈。

北极圈 北纬66°34'的纬线。

南极圈 南纬66°34'的纬线。

后两条释文是一种直接表示法，直接用纬度表示，一目了然。前一条释文是一种间接表示法，用距离极点的纬度差表示，转了一个弯，不那么直观，而且还隐含了南北极纬度为90°的地理知识。这对使用该词典的读者来说，提高了使用者的使用门槛，即需要掌握相关知识点才不会引起误解。

所以对于前一条，改为如下的释文就比较通俗简洁:

极圈 地球上纬度66°34'的界限。在南半球为南极圈，在北半球为北极圈。

5．运用直观的插图

这个问题主要是探讨用直观的美术图，还是用规范的工程制图。

作为理工科类的专科词典，特别是工科类的，会涉及工作原理、内部结构等示意图，是采用标准的工程制图规范画法，还是采用一般的美术透视画法，并不能一概而论。对工程技术专业工作者而言，图纸就是工程界的通用语言，就像音乐是全世界的通用语言一样。而对于专科词典来说，释文是第一位的，插图只是补充文字说明之不足，起简化文字或使条目增辉的作用，是第二位的，不能用专业的标准来要求专科词典。

6．专科词典介绍的是一个概念

专科词典是以条目的形式介绍学科知识、表达术语概念的。就知识点而言是离散的、跳跃式的，而教科书对内容的介绍是循序渐进式的、模块化的。

如同样两条词目名称都是“××方程”，其内涵不同，写法也不同，举例如下:

纳维-斯托克斯方程 简称“N-S方程”。黏性流体动量守恒的运动方程。由一组二阶偏微分方程组成，表达式为:

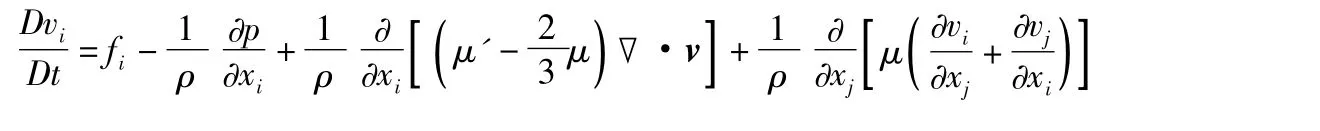
式中 为速度矢量i为速度矢量的坐标分量 ρ为流体密度 为压力i为质量力分量 μμ分别为黏性系数和第二黏性系数(又称“体变形黏性系数”);▼为哈密顿算子;i，j=1，2，3。

洛伦兹方程 1963年美国气象学家洛伦兹(Edward Norton Lorenz，1917—2008)建立的描述天气变化的一个三阶常微分方程组。通过对该方程的数值计算发现了混沌现象。洛伦兹的工作对非线性动力学作出了重要贡献，提供了一个具有分岔和混沌运动性态的数学模型。蝴蝶效应就是洛伦兹方程的解所得到的吸引子的形象描述。

上述第一条“纳维-斯托克斯方程”虽由纳维于1821年和斯托克斯于1845年分别建立，在数值解方面获得可喜成果，但至今仍没有彻底解决。该方程是美国克雷数学研究所于2000年5月24日在巴黎法兰西学院宣布的七个“千年数学难题”中的一个。方程的本身相对重要，所以列出。而第二条的“洛伦兹方程”其重点在于通过对该方程的数值计算发现了混沌现象，即“蝴蝶效应”，因而对非线性动力学做出了贡献。方程的本身相对而言是次要的，所以没有列出。由美国房利美和房贷美公司破产引发的全球性金融风暴，就是“蝴蝶效应”的一个例子。

结 语

辞典释文的深入浅出不能仅仅片面地理解为用普通语词替代专业术语来阐释高深的科学理论，而应当用普通读者能够理解的概念或已经掌握的知识来了解、学习、掌握新的知识。科学普及工作需要将深奥的科学知识和原理用通俗的语言来表达，使之飞入寻常百姓家。所以，使专科词典的释文深入浅出是每一个编纂者责无旁贷、应该为之努力的方向，否则又有多少读者能够理解高深难懂的知识呢?

1．大辞海编辑委员会．大辞海·数理化力学卷．上海:上海辞书出版社，2005．

2．《力学词典》编辑部．力学词典．北京:中国大百科全书出版社，1990．

3．徐庆凯．专科词典论．上海:上海辞书出版社，2011．