实对称阵正交相似对角化方法及其优化

胡国专

（淮阴工学院 数理学院，江苏 淮安 223003）

据矩阵对角化理论,n阶方阵A相似于对角阵 (常称A可对角化)的充要条件为A有n个线性无关的特征向量,对实对称阵进一步有如下定理[1]:

定理1 实对称阵A的属于不同特征值的特征向量是线性无关的且是正交的.

定理2 设A是n阶实对称阵,λ1,λ2,…,λr是矩阵A的全部互异特征值,λi的重数为,且齐次线性方程组(λiE-A)x=0一定有ki个彼此正交的解向量.

定理3 设A是n阶实对称阵,则存在正交矩阵Q使得

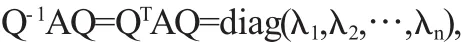
其中 λ1,λ2,…,λn是 A的特征值,Q的列向量组 e1,e2,…,en是分别对应于λ1,λ2,…,λn的A的标准正交的特征向量组.

因此,实对称阵一定可以对角化且可以正交相似对角化,其中怎样求出正交矩阵Q是关键,一般代数教材上给出的经典方法步骤为:

第一步:求出矩阵A的全部互异特征值；

第二步:对于每一特征值λi,解齐次线性方程组(λiE-A)x=0得对应的特征向量；

第三步:将求得的特征向量组化为与之等价的标准正交向量组；

第四步:写出正交矩阵 Q 及 QTAQ=diag(λ1,λ2,…,λn).

此方法严谨规范,易于掌握,但步骤多,计算量大,在特征值出现重根的情况下,需用施密特(Schmidt)正交化方法求正交特征向量组,过程繁琐,限于篇幅,在此不再举例.本文在此基础上作进一步的讨论,优化上述方法中某些步骤或过程,用相关实例验证与比较,探寻更便捷实用的对角化方法.

优化1 线性方程组法

由定理2我们知道,实对称阵A特征值λi的重数为ki(ki≥2)时,则齐次线性方程组(λiE-A)x=0 一定有 ki个彼此正交的特征向量,结合文[2],对重特征值λi,可以用解线性方程组的方法求出,避开用施密特正交化的方法,对单特征值仍用常规解法求其特征向量,求解步骤如下:

第一步:求(λiE-A)x=0的一个非零解α1;

依此类推,直至求出实对称阵A属于特征值λi的ki个两两正交的特征向量.考虑到计算量的问题,特别当实对称阵有n-1重特征值（这种情况很常见）时,可以将此方法优化为如下的赋值法求其特征向量.设λ为实对称阵A的n-1重特征值,方程组(λE-A)x=0的同解方程组只有一个方程,设为

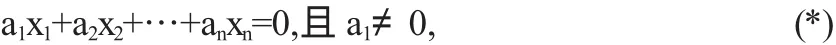
取x1=b1≠0,x3=x4=…=xn=0,得第一个特征向量α1=(b1,b2,0,…,0)T,为求与 α1正交的特征向量 α2,取 x4=x5=…=xn=0,x1=b1(保持α1的第一个分量不变),α2的第二个分量满足b12+b2x2=0,即满足[α1,α2]=0,再代入方程(*)得第二个特征向量α2=(b1,b2',b3,0…,0)T, 为求与 α1、α2都正交的特征向量 α3,取x1=b1,x2=b2'(保持 α2的前两个分量不变),x5=…=xn=0,α3的第三个分量满足 b12+(b2')2+b3x3=0,即满足[α2,α3]=0,再代入方程(*)得第三个特征向量α3=(b1,b2',b3',b4,0,…,0)T,依此类推,可以求出实对称阵A属于λ的全部n-1个两两正交的特征向量.

用解线性方程组的方法求A的全部n个两两正交的特征向量,主要优化了经典方法中的第二、三两个步骤,当有重特征值时,把线性方程组的求解与特征向量的正交化合二为一,特别是避开用较复杂的施密特正交化方法,起到一定的简化作用.

得A的特征值λ1=-1(二重),λ2=5,属于特殊情形,

当λ=-1时,(-E-A)x=0对应的同解方程为x1+x2+x3=0,取x1=1,x3=0,

得第一个特征向量α1=(1,-1,0)T,与之正交的α2的第一个分量取1,第二个分量应满足12-x2=0,得x2=1,从而得第二个特征值向量α2=(1,1,-2)T；

当λ=5时,(5E-A)x=0对应的齐次线性方程组为

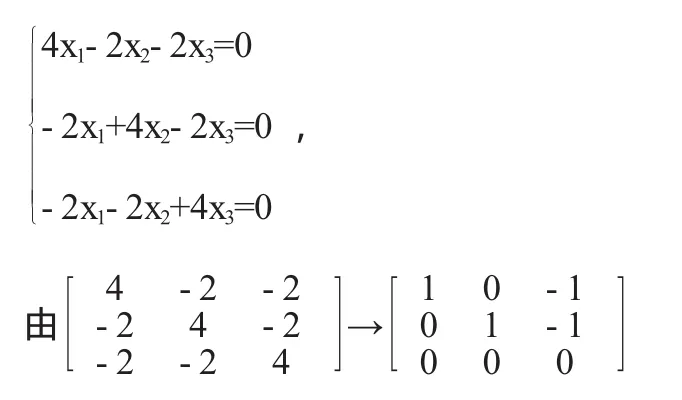
得第三个特征向量 α3=(1,1,1)T,再将 α1、α2、α3单位化得

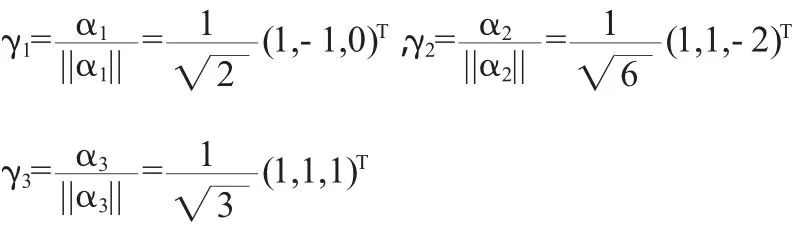
从而得正交阵 Q=(γ1，γ2，γ3)=diag(-1,-1,5).

优化2 积矩阵法

由文[3]有如下结论:

设 λ1,λ2,…,λr是实对称阵 A 的全部互异特征值,λj的重数为 kj(j=1,2,…,r),则矩阵的列向量中恰有对应于λj的kj个线性无关的特征向量.

这为我们求特征向量开辟了新的思路,对每一个特征值λj,构造含其它特征值的矩阵积的新矩阵Wj,通过求此矩阵的极大无关列组的方法求特征向量,代替求齐次线性方程组基础解系的工作,简化了解题过程,为方便叙述,不妨称之为积矩阵法.本方法主要优化经典方法中的第二步,特别当实对称阵只有2个相异特征值的情况下,不仅不需要解方程组,而且不需要算矩阵的乘积就可以把对应于不同特征值的特征向量快速求出.

例2 用积矩阵法解例1.

解 由例1知A的特征值λ1=-1(二重),λ2=5,

用Schmidt正交化方法,先正交化,有

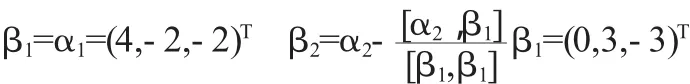
再将 β1,β2单位化,得

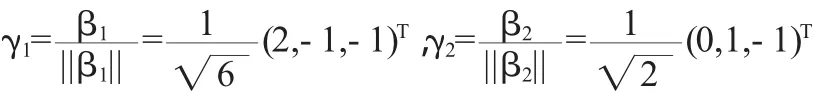
得特征向量α3=(-2,-2,-2)T,再单位化得则 Q=(γ1,γ2,γ3).

优化3 对称变换法

对称变换是指对矩阵每作一次初等行变换,同时对列再作一次相同的初等列变换,其模型为:

由文[4]有如下结论:

设A为实对称阵,若λE-A经一系列对称的初等变换化为对角阵QT(λE-A)Q=λE-B,且每次对称变换的倍乘系数均不含λ,即A为不含λ的初等矩阵之积,则B的主对角线上的元素必为A的全部特征值,Q必为正交阵.

对称变换法关键是用对称的初等变换将λE-A化为对角阵,回避了常规解法中求特征值要解高次方程,求特征向量要依据特征值多次解线性方程组的繁难过程,从某种程度上讲是对传统方法的颠覆,起到较好的简化作用,显得简捷高效.

例3 用对称变换法解例1(注:对称变换记号中的r表示行,c表示列).

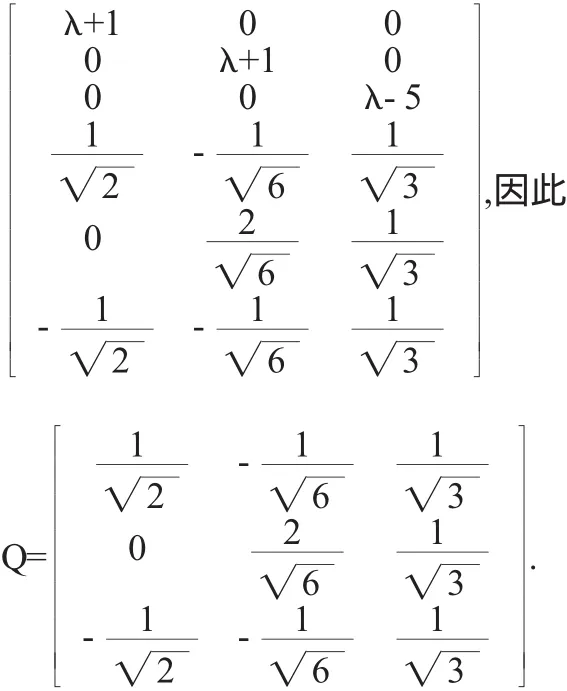
纵观本文所探究的实对称阵正交相似对角化的四种方法,线性方程组法、积矩阵法、对称变换法从不同角度对经典方法进行了优化,但每种方法也会有一定的弊端,没有十全十美的方法.线性方程组法省去施密特正交化步骤,但可能要解多个线性方程组；积矩阵法改解线性方程组为求矩阵的极大无关列,但可能要计算多个矩阵的乘积；对称变换法回避了常规解法中求特征值与特征向量的繁琐过程,但是在每次对称变换时,要求倍乘系数均不含λ,从而增加对称变换化λE-A为对角阵的难度.文中用三种方法解同一个题,是为便于比较,可以看出,三种解法从不同角度优化了传统方法,各有千秋.因此,在应用中,要结合实对称阵的阶数、特征值的个数与重数等不同情形灵活选择方法,从而起到事半功倍的作用.

〔1〕陈建龙,等.线性代数[M].北京:科学出版社,2007.123-124.

〔2〕钟甲祥.实对称矩阵的对角化探研[J].柳州师专学报,1994（1）:24-27.

〔3〕李佩贞.矩阵的对角化与相似变换矩阵[J].中山大学学报论丛,2000,20(4):248-251.

〔4〕付立志，等.对称矩阵对角化的正交变换模型[J].河南科学,2008,26(2):135-147.