一类带有扩散的Lotka-Volterra竞争系统的共存态

陕西师范大学 数学与信息科学学院，西安 710062

陕西师范大学 数学与信息科学学院，西安 710062

1 引言

运用反应扩散方程研究种群动力学行为是目前人们关注的一个基本问题。在过去的几十年中，人们应用数学方法研究了带有各种边界条件的物种相互作用的许多反应扩散系统，比如 Lotka-Volterra系统[1-6]，Leslie-Gower系统[7-8]，Sel'kov系统[9-10]以及Brusselator系统[11-12]等。在这些文献中，作者运用不同的方法分析了相关模型的动力学行为，包括模型解的存在性、不存在性、有界性、分歧、稳定性以及渐近性等性质，并获得了许多有价值的经典结果。

在众多关于Lotka-Volterra模型的文献中，反应项是二次的相对来讲比较常见。本文讨论下面带有三次反应项的Lotka-Volterra竞争反应扩散系统：

其中Ω⊂ℝN为带有光滑边界∂Ω的有界开区域，u=u(x,t)，v=v(x，t)表示两竞争物种的数量；d1，d2表示 u，v 的扩散率；a，e表示u，v的出生率；b，g表示u，v的自我调节率；c，f描述的是u，v之间的竞争关系。所有的参数都是正常数，齐次边界条件意味着两物种在栖息地边界的种群密度为零。考虑到实际意义，只关心系统（1）的非负解。关于反应函数是3次项的Lotka-Volterra型竞争系统的其他研究结果可参见文献[13-16]等。

从生物学上来讲，可对系统（1）作如下解释：函数a-bu2，fu2以及 e-gv2，cv2描述的是物种 u与 v之间以及同一物种内部不同个体间的相互作用的关系。首先，f＞b且c＞g表示两不同物种之间的相互作用强于同一物种内部个体之间的相互作用。因此，当 f＞b且c＞g时系统（1）是一个强竞争系统。其次，当 f＜b且c＜g时表示两不同物种之间的相互作用弱于同一物种内部的相互作用。因此，当 f＜b且c＜g时系统（1）是一个弱竞争系统。再次，当 f=b且c=g时，表示两不同物种间的相互作用与同一物种内部的相互作用的强弱程度几乎相同。

如果考虑u，v只与x有关的情形，那么寻求系统（1）的平衡态解就是很自然的。同时，如果这样的解是严格正的，则通常被称为共存态。本文的主要目的是讨论系统（1）共存态的存在性，也就是讨论下面椭圆型系统：

的古典解的存在性。

为方便起见，先给出一些已知结果。

用λ1(q)表示特征值问题

的主特征值，则 λ1(q)关于 q 递增。记 λ1(0)= λ1，则 λ1＞ 0[3]。考虑下面的非线性边值问题：

众所周知[1，3]，如果 a＜λ1(q)，那么 u≡0 是式（3）的唯一非负解；反之，如果a＞λ1(q)，那么式（3）存在唯一正解。

2 共存态的存在性

利用文献[2]中的主要结果考虑系统（2）共存态的存在性。为简单起见，不妨取d1=d2=1（事实上，如果适当调整系统中的参数，那么两物种的扩散系数就可转化为1）。

给定广义Lotka-Volterra椭圆系统：

其中 Ω，u，v的含义与第1章相同，函数 h1，h2，h3，h4满足：

（1）h1，-h2，h3，-h4∈C(Ω)是 [0，∞)上的非增函数且h1(0)＞0，h3(0)＞0，h2(0)=h4(0)=0 。

（2）存在常数 c1，c2使得当 u＞c1时 h1(u)＜0，v＞c2时h3(v)＜0。

引理2.1[2]设h(u)为[0，∞)上的严格递减光滑函数且存在常数 c0＞0使得当 u≥c0时 h(u)≤0。若 h(0)＞λ1，则边值问题：

有唯一正解。若h(0)≤λ1，则0是唯一非负解。

由引理2.1知，当 h1(0)＞λ1，h3(0)＞λ1时，系统（4）存在半平凡解 (u*，0)与 (0，v*)，其中 u*，v*分别满足问题：

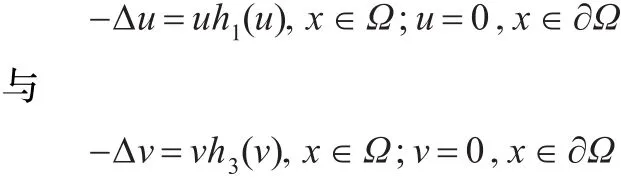
在文献[2]中，(u*，0)与 (0，v*)在讨论系统（4）的正解的存在性时，起着相当重要的作用，相关的主要结论为：

引理2.2[2]设 h1(0)＞λ1，h3(0)＞λ1。若主特征值 λ1(Δ+ (h1(0)-h2(v*)))与 λ1(Δ+(h3(0)-h4(u*)))有相同的符号，则系统（4）存在正解。

比较系统（2）与（4），对于系统（2）来说，很显然：

定理2.1 设 a＞λ1，e＞λ1。若主特征值 λ1(Δ+(a-cv*2))与 λ1(Δ+(e-fu*2))有相同的符号，则系统（2）存在正解。

定理2.2 设 a＞λ1，e＞λ1。若：

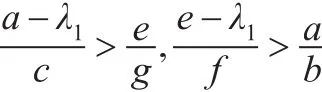
则系统（2）存在正解。

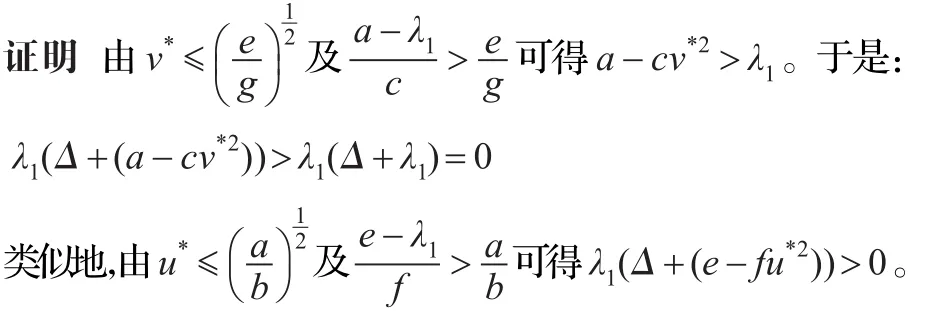
因此，由定理2.1知系统（2）存在正解。证毕。

定理2.3设下面条件成立：

则系统（2）存在正解。

证明由引理2.1知，系统（2）存在解 (u*，0)，(0，v*)。

首先，有：

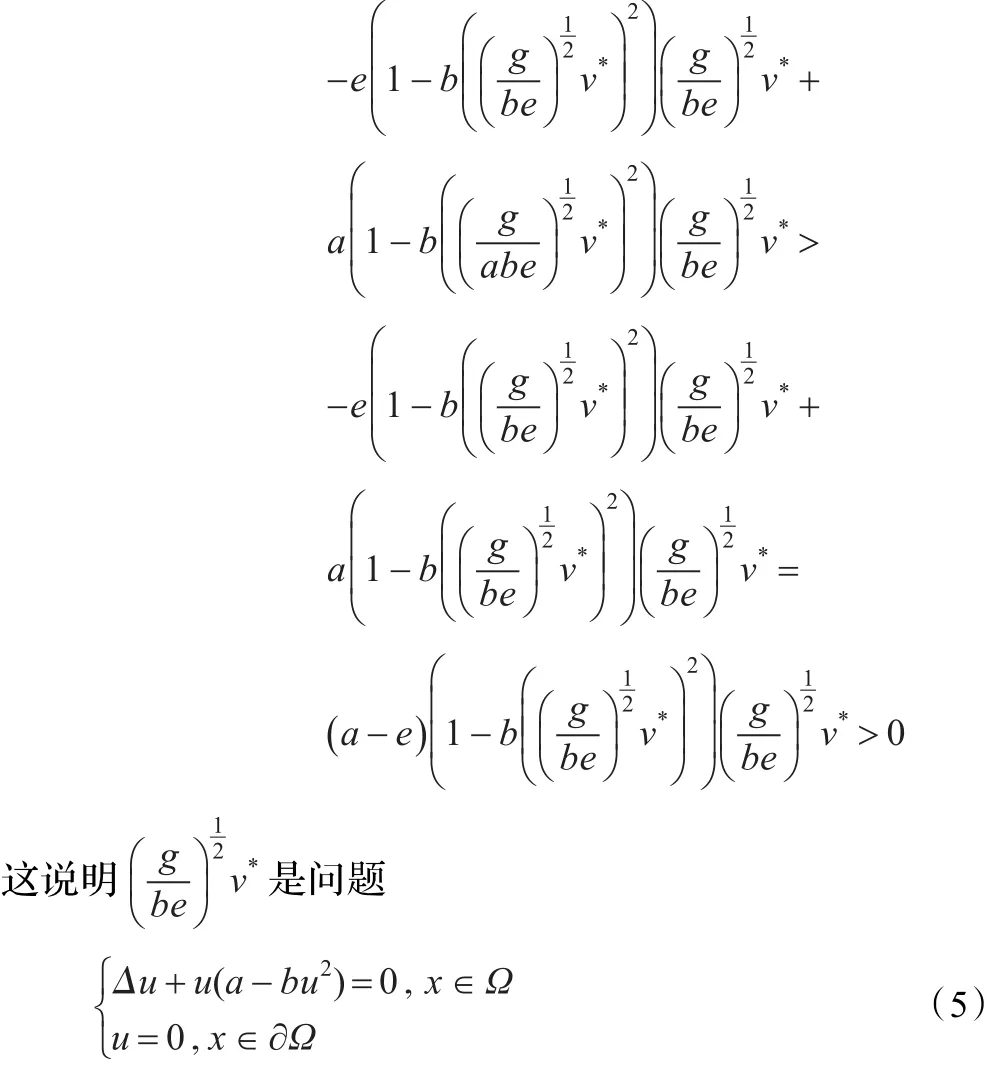
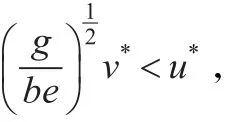
于是，λ1(Δ+(a-cv*2))与 λ1(Δ+(e-fu*2))有相同的符号，从而式（2）存在正解。证毕。

定理2.4若a=e，则系统（2）存在正解当且仅当下面条件之一成立：

证明 考虑情形（1）。显然，式（2）存在解 (u*，0)，(0，v*)。由于 u*满足式（5）且 u*＞0，因此 λ1(Δ+(a-bu*2))=0。类似地，λ1(Δ+(e-gv*2))=0. 由 b＞f，c＜g可得：

同样，对情形（2），（3）可得：

由定理2.1知，系统（2）存在正解。

反过来，设 (u，v)是式（2）的正解，则

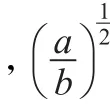
给式（2）的两个方程分别同乘v和u然后相减，再在Ω上积分可得：

由于u，v＞0，于是该等式表明要么(f-b)u2+(g-c)v2在 Ω上恒为零，要么在 Ω上改变符号。这意味着b=f，c=g 或 b＞f，c＜g 或 b＜f，c＞g 。这说明若系统（2）有正解，那么条件（1），（2），（3）中必有一个成立。证毕。

3 结语

反应扩散方程遍及许多学科，可以说反应扩散方程是刻画自然界各种现象及运动规律的基本方程之一。本文着眼于反应扩散方程在生态学领域的应用，考虑处于同一环境中不同种群间的共存问题。对于生活在同一生态环境中的不同种群来说，物种间的共存与灭绝问题是人们研究生态系统的一个永恒的主题。物种间竞争关系的强弱直接影响着物种适应环境变化的能力。文中考虑的是带有高次功能反应项的扩散模型，运用非线性分析方法和二阶椭圆型偏微分方程理论着重考察了具有竞争关系的两种群能够共存的条件，得到了一些有益的结果。

[1]Blat J，Brown K J.Global bifurcation of positive solutions in some systems of elliptic equations[J].SIAM Journal on Mathematical Analysis，1986，17：1339-1352.

[2]Li L，Logan R.Positive solutions to general elliptic competition models[J].Differential and Integeral Equations，1991，4：817-834.

[3]Cosner R C，Lazer A C.Stable coexistence state in the Volterra-Lotka competition model with diffusion[J].SIAM Journal on Applied Mathematics，1984，44：1112-1132.

[4]Wang L，Li K.On positive solutions of the Lotka-Volterra cooperating models with diffusion[J].Nonlinear Analysis，2003，53：1115-1125.

[5]Roeger L I W.A nonstandard discretization method for Lotka-Volterra models that preserves periodic solutions[J].Journal of Difference Equations and Applications，2005，11：721-733.

[6]Jia Y，Wu J，Nie H.Coexistence states of a three-species cooperating model with diffusion[J].Applicable Analysis，2011，90：1185-1202.

[7]Haque M，Venturino E.Effect of parasitic infection in the Leslie-Gower predator-prey model[J].Journal of Biological Systems，2008，16：425-444.

[8]Aisharawi Z，Rhouma M.Coexistence and extinction in a competitive exclusion Leslie-Gower model with harvesting and stocking[J].Journal of Difference Equations and Applications，2009，15：1031-1053.

[9]Wang M.Non-constant positive steady states of the Sel'kov model[J].Journal of Differential Equations，2003，190：600-620.

[10]Lieberman G M.Bounds for the steady-state Sel'kov model for arbitrary pin any number of dimensions[J].SIAM Journal on Mathematical Analysis，2005，36：1400-1406.

[11]Kuptsov P V，Kuznetsov S P，Mosekilde E.Particle in the Brusselator model with flow[J].Physics D，2002，163：80-88.

[12]Golovin A A，Matkowsky B J，Volpert V A.Turing pattern formation in the Brusselator model with superdiffusion[J]. SIAM Journal on Applied Mathematics，2008，69：251-272.

[13]Taylor A，Crizer A.A modified Lotka-Volterra competition model with a non-linear relationship between species[J].Rose-Hulman Undergraduate Mathematics Journal，2005，6：1-14.

[14]Chattopadhyay J.Effect of toxic substances on a two-species competitive system[J].Ecological Modelling，1996，84：287-289.

[15]Zhen J，Ma Z.Periodic solutions for delay differential equations model of plankton allelopathy[J].Computers and Mathematics with Applications，2002，44：491-500.

[16]Kan-on Y.Global bifurcation structure of stationary solutions for a Lotka-Volterra competition model[J].Discrete and Continuous Dynamical Systems，2002，8：147-162.

一类带有扩散的Lotka-Volterra竞争系统的共存态

贾云锋，王 莹

JIAYunfeng,WANG Ying

College of Mathematics and Information Science,Shaanxi Normal University,Xi’an 710062,China

The steady-state solutions of a Lotka-Volterra competition ecological system with cubic functional responses and diffusion are concerned.With the assistance of the spectrum analysis and the upper-lower solutions,a few sufficient conditions for the existence on coexistence of the system are presented.

Lotka-Volterra competition system;coexistence;principal eigenvalue;upper-lower solution

考虑了一类带有三次功能反应项和扩散的Lotka-Volterra竞争生态系统的平衡态解。运用谱分析的方法，通过构造上下解，给出了系统存在共存态的一些充分性条件。

Lotka-Volterra竞争系统；共存态；主特征值；上下解

A

O175.2

10.3778/j.issn.1002-8331.1203-0402

JIA Yunfeng,WANG Ying.Coexistence of Lotka-Volterra competition system with diffusion.Computer Engineering and Applications,2013,49（11）：35-37.

国家自然科学基金（No.11001160）；陕西师范大学中央高校基本科研业务费专项资金项目（No.GK201002046）。

贾云锋（1972—），男，博士，副教授，主要研究领域为微分方程理论及应用、数值计算；王莹（1988—），女，硕士研究生，主要研究领域为微分方程理论及应用。E-mail：jiayf@snnu.edu.cn

2012-03-19

2012-07-03

1002-8331（2013）11-0035-03