基于ε-互模拟的软件近似正确性模型
1.淮北师范大学 计算机科学与技术学院,安徽 淮北 235000
2.上海市高可信计算重点实验室,上海 200062
3.淮北师范大学 数学科学学院,安徽 淮北 235000
1.淮北师范大学 计算机科学与技术学院,安徽 淮北 235000
2.上海市高可信计算重点实验室,上海 200062
3.淮北师范大学 数学科学学院,安徽 淮北 235000
1 引言
软件正确性是软件工程的重要内容,是软件可信性的重要属性。对软件正确性进行研究可以为提高软件质量提供保证。软件正确性主要表现为软件的执行能否符合人们的预期。一般地,软件的执行抽象为软件的实现,人们的预期抽象为软件的规范。进而软件正确性表示为软件的实现与规范之间的关系。这种关系借助于进程代数中的各种理论来描述:如ACP[1],Communicating Sequential Process(CSP)[2],Calculus of Communicating Systems(CCS)[3]等。在R.Milner提出的CCS语言(也称为通信系统演算)中,各种进程之间的等价关系是其主要内容,如强互模拟和弱互模拟、迹等价及观测等价等。把规范(specification)和实现(implementation)抽象为两个进程,如果软件规范和实现之间存在某种等价关系,则软件是正确的。在文献[4]中,应明生给出了这些等价关系的无限演化过程,定义了强互模拟极限、弱互模拟极限和迹极限等,从而建立了CCS语言的极限理论。为了描述在一定环境下软件实现的无限演化,在文献[5-6]中,作者基于ε-参数化互模拟,提出了ε-参数化极限互模拟和参数化互模拟极限,建立了ε-参数化互模拟的极限理论和拓扑理论。为了度量在拒绝环境下软件实现与规范之间的近似程度,在文献[7]中作者建立了三分之二互模拟的度量理论。
而在一些复杂的软件系统中,存在一定的概率现象,为了描述这种复杂系统的概率信息,已经出现了很多概率进程代数模型[8-10]。像CCS一样,每个模型都有概率互模拟等价[11]。如 A.Giacalone,C.C.Jou 和 S.A.Smolka提出的 ε-互模拟等价,其以生长概率模型(generative probabilistic model)[12]为基础描述了进程之间的几乎处处相等。例如,一个软件的规范用一个概率进程表示为P=0.4a.0+0.6b.0,其实现用概率进程表示为Q=0.400 1a.0+0.599 9b.0。尽管实现与规范直接没有完全匹配,但是执行相同动作的概率是非常接近的。事实上,在概率情况下进程之间的几乎处处相等比进程的等价更加有用,因为等价的要求太严格了,在实际中很难达到。在实际应用中,如果规范中包含一些概率信息,而在开发实现过程中,若适当的误差是被允许的,则可以选择ε-互模拟来验证软件实现与其规范的关系。一般地,初次获得的实现未必能够符合要求,进而需要不断地修改实现,使其越来越符合要求。由此得到一个实现的进化序列。但是,当开发过程由几个团队共同完成,在同一时间,几个团队都对实现进行了修改,由此得到的实现改进过程不再是一个序列,而是一个偏序,为了描述这种情况,可以利用拓扑中的网来描述进程。本文利用ε-互模拟,试图建立实现进化过程的收敛机制。对实现的进化过程进行抽象刻画,可以为实际的软件开发提供指导,帮助软件开发者检查开发过程是否朝着正确的方向发展。同时在理论上进一步丰富了软件的形式化理论。
在本文中引入ε-极限互模拟和ε-互模拟极限,其刻画了软件的规范是其实现的极限。给出ε-极限互模拟的例子,证明ε-互模拟极限的唯一性,ε-互模拟极限与ε-互模拟的相容性等性质。
2 预备知识
本章主要介绍概率进程代数(PCCS)的一些基本知识以及拓扑学中网的一些基本内容。首先,介绍概率进程代数的语法和语义,这部分内容主要来自文献[12]。
定义2.1[12]概率进程表达式集合ε是包含0,X和下面表达式的最小集合:
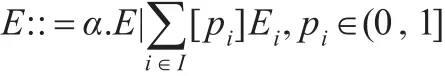
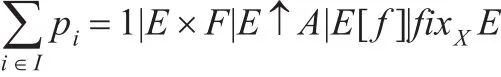
定义2.2[12]PCCS的操作语义是以概率导出为基础的,由一组推理规则构成,其形式与Plotkin的相同。具体规则如下:
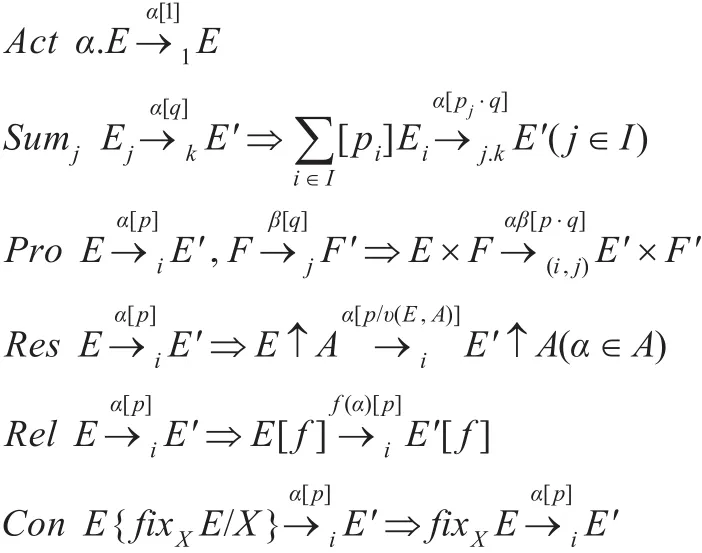
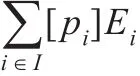
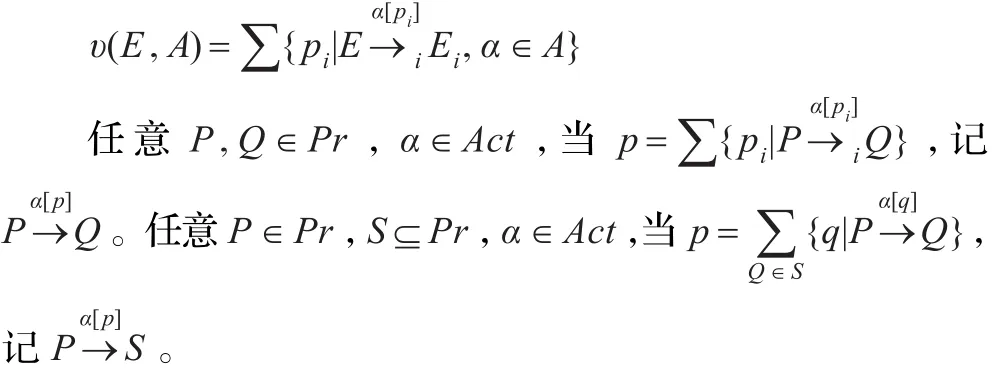
若任意α∈Act,P至多有一个类型为α的概率导出,则称P是确定性概率进程。所有确定性概率进程的集合记为DPr。
定义2.3(ε-互模拟)[12]令 ε∈[0,1),在集合 DPr上的一个二元关系 Rε⊆DPr×DPr称为ε-互模拟,若满足:如果(P,Q)∈Rε蕴含任意 α∈Act。
3 ε-极限互模拟
软件在设计过程中需要不断地对其进行修改,在修改过程中得到一系列实现版本,每个版本与规范之间都可以用ε-互模拟来刻画。但是,修改过程是一个无限过程,其最终目的是规范。本章定义ε-极限互模拟,用来刻画软件实现的修改过程中得到这些实现与规范之间的关系,并给出几个ε-极限互模拟的例子。
定义3.1 令ε∈[0,1)。DPr和DPrN上的二元关系Sε⊆ DPr×DPrN被称为 ε-极限互模拟,若满足任意α∈Act,(P,{Qn:n ∈ D})∈ Sε。

从定义上可以看出,ε-极限互模拟是ε-互模拟的动态演化形式。若确定性概率进程P和确定性概率进程网{Qn:n∈D}是ε-互模拟相关,则P是{Qn:n∈D}极限行为。语句(1)表示,若P以概率 p执行动作α,则{Qn:n∈D}最终能执行α且其执行α的概率与 p最多相差ε。语句(2)是说若{Qn:n∈D}经常以概率qn执行动作α,则P也能执行该动作且执行α的概率与qn的距离不超过ε。
例3.1令规范P=0.4a.0+0.6b.0,获得的一系列实现为:
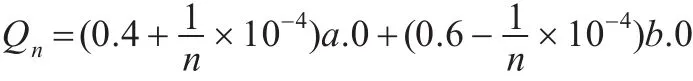
如,第一次获得的实现:
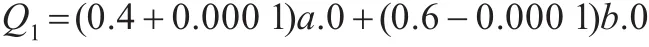
第二次修改获得的实现:
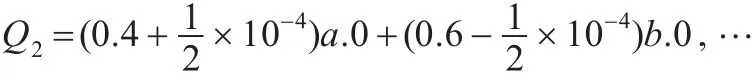
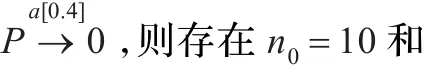
已知在确定概率进程上的恒等关系 Iden是ε-互模拟,下面将此关系延拓到ε-极限互模拟上。这个关系也说明了在实际开发软件时,若初次开发获得的实现与规范之间符合要求,则这样的实现不需要修改。令
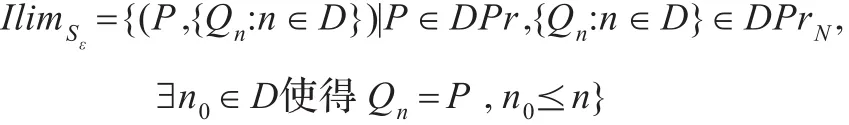
命题3.1 令 ε∈[0,1),Sε⊆DPr×DPrN,则 IlimSε是 ε-极限互模拟。
下面的例子说明在软件开发时,若获得的一系列实现与规范之间满足要求,则在这些实现序中必然有一部分满足要求。


证明“⇒”显然。
“⇐”假设 (P,{Rm:m∈C})∈sub(Sε),则存在 (P,{Qn: n∈D})∈Sε使得{Rm:m∈C}是{Qn:n∈D}的子网,即存在映射 N:C→D使得(C,N)是 D的共尾且,任意m∈C,Rm=QNm。一直假设N是增加的,即m1≤m2蕴含N(m1)≤N(m2)。

命题3.3 如果Sε是 ε-极限互模拟,则 sub(Sε)也是ε-极限互模拟。

4 ε-互模拟极限
在本章中,为了描述软件修改过程的收敛机制,提出ε-互模拟极限的定义。指出软件的规范在概率互模拟下是其实现的极限形式。
定义4.1(1)令ε∈[0,1),P∈DPr,{Qn:n∈D}∈DPrN。如果存在 ε-极限互模拟 Sε使得 (P,{Qn:n∈D})∈Sε,则称


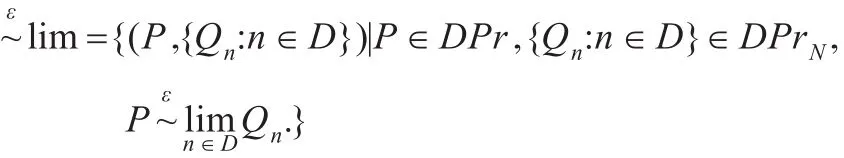
则由命题3.4可知:

是最大的ε-极限互模拟。
例4.1考虑带有概率信息的缓冲器,Buffn(k),n∈ω,k≤n。令
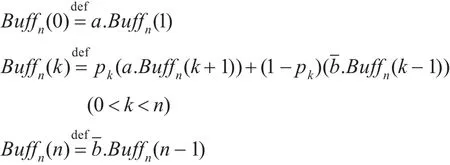
缓冲器Buffn(k)的存储能力是n,k是临时存储消息的数量。若缓冲器不满,即k<n,发送者可以一直以概率pk给Buffn(k)发送消息,当缓冲器不空时,即k>0,接收者可以一直从缓冲器Buffn(k)上以概率1-pk接收到消息。下面证明在ε-互模拟下有界概率缓冲器的极限是无界概率缓冲器。定义无界概率缓冲器Buff∞(k)。令
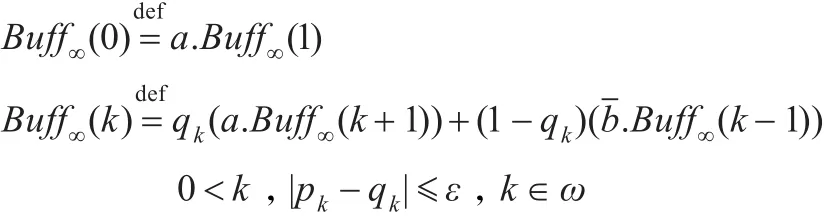
这个例子是说有界概率缓冲器的极限是无界概率缓冲器。 Buffn(k)和 Buff∞(k)之间的不同在于 Buff∞(k)是无限的,因此发送者不需要考虑缓冲器中已有消息的数量,可以一直发送消息。
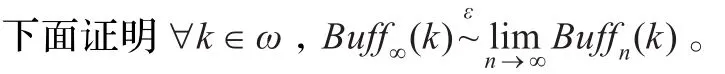
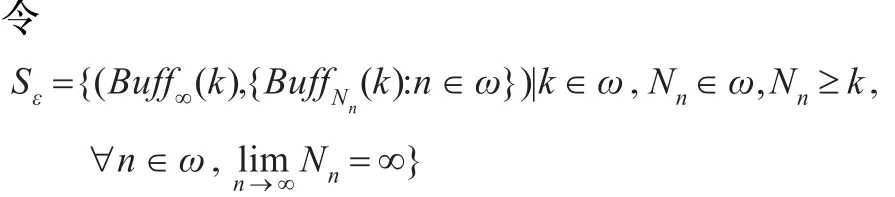



命题4.3表明了ε-互模拟极限与ε-互模的相容性。在实际中,若两个团队开发时获得的实现非常相似,则他们开发时所依据的规范是同一个规范。
命题4.4给出了ε-互模拟极限的唯一性。也表明了在实际开发中开发实现必须依据一个规范,不能依据不同的规范开发同一个软件。
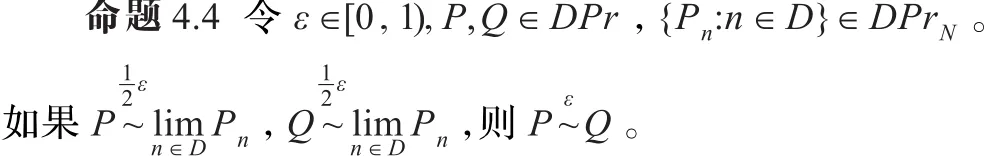
5 结论
在本文中主要以PCCS语言为基础,讨论了进程的ε-互模拟的极限行为,定义了ε-极限互模拟,并在此基础上建立了ε-互模拟极限。同时证明了一些性质。为了更好地从数学角度理解和分析进程的动态特性,在接下来的研究中将给出ε-互模拟的拓扑理论。
[1]Baeten J C,Weijland W P.Process algebra[M].Cambridge:Cambridge University Press,1990.
[2]Hoare C A R.Communicating sequential processes[M].New York:Prentice Hall,1985.
[3]Milner R.Communication and concurrency[M].New York:Prentice Hall,1989.
[4]Ying M S.Topology in process calculus:approximate correctness and infinite evolution of concurrency programs[M].Berlin:Springer-Verlag,2001.
[5]Ma Y F,Zhang M.Topological construction of parameterized bisimulation limit[C]//Electronic Notes in Theoretical Computer Science.Amsterdam:Elsevier Science,2009,257:57-70.
[6]Ma Y F,Zhang M.Parameterized bisimulation infinite evolution mechanism[C]//3rd IEEE International Symposium on Theoretical Aspects of Software Engineering,Tianjin,China.Los Alamitos,CA:IEEE Computer Society,2009:299-300.
[7]马艳芳,张敏,陈仪香.基于环境的软件正确性形式化描述[J].山东大学学报:理学版,2011,46(9):22-27.
[8]Frank B,James W.Approximating and computing behavioural distances in probabilistic transition systems[J].Theoretical Computer Science,2006,360(1/3):373-385.
[9]Song L,Deng Y X,Cai X J.Towards automatic measurement of probabilistic processes[C]//7th International Conference on Quality Software,Portland.Washington:IEEE Computer Society, 2009:50-59.
[10]Deng Y X,Glabbeek R,Hennessy M,et al.Testing finitary probabilistic processes[C]//Lecture Notes in Computer Science 5710:The 20th International Conference on Concurrency Theory,Bologna,Italy.Berlin:Springer-Verlag,2009:274-288.
[11]Larsen K G,Skou A.Bisimulation through probabilistic testing[J]. Information and Computation,1991,94(1):1-28.
[12]Giacalone A,Jou C C,Smolka S A.Algebraic reasoning for probabilistic concurrenct systems[C]//Lecture Notes in Computer Science 494:IFIP TC2 Working Conference on Programming Concepts and Methods,Tiberias.Berlin:Springer-Verlag,1990:443-458.
[13]Milner R.Calculi for synchrony and asynchrony[J].Theoretical Computer Science,1983,25:267-310.
[14]Kelly J L.General topology[M].Germany:Springer-Verlag,1975.
[15]Engelking R.General topology[M].Poland:Polish Science,1977.
基于ε-互模拟的软件近似正确性模型
马艳芳1,2,陈 亮3
MAYanfang1,2,CHEN Liang3
1.School of Computer Science and Technology,Huaibei Normal University,Huaibei,Anhui 235000,China
2.Shanghai Key Laboratory of Trustworthy Computing,Shanghai 200062,China
3.School of Mathematical Sciences,Huaibei Normal University,Huaibei,Anhui 235000,China
The correctness of software is a key attribution for trustworthiness of software.In the real development and design, the software is modified constantly in order to get correctness,and the software is correct more and more.This paper focuses on the dynamic characterization of correctness.Based on ε-bisimulation of probabilistic process algebra,ε-limit bisimulation is defined which reflects the relation between implementation and its specification,and some specialε-limit bisimulations are showed.ε-bisimulation limit is presented,which states that specification is the limit of implementations.Some important properties are proved.
trustworthiness;correctness;formalization;process algebra
软件正确性是软件可信性的重要属性。在实际软件开发和设计中,需要不断地对软件进行修改,从而软件越来越正确。为了讨论软件的动态近似正确性,基于概率进程代数的ε-互模拟,建立软件越来越正确的形式化描述。定义ε-极限互模拟,用来反应软件实现与规范之间的关系,给出一些特殊的ε-极限互模拟。提出ε-互模拟极限,用其刻画规范是软件实现的极限形式,同时证明ε-互模拟极限的一些性质。
可信性;正确性;形式化;进程代数
A
O159;TP301
10.3778/j.issn.1002-8331.1211-0125
MA Yanfang,CHEN Liang.Model of software approximate correctness underε-bisimulation.Computer Engineering and Applications,2013,49(11):15-19.
安徽省自然科学基金(No.1308085QF117);安徽高校省级自然科学研究重点项目(No.KJ2011A248);安徽高校省级自然科学研究一般项目(No.KJ2012Z347);上海市高可信计算重点实验室开放项目(No.07DZ22304201004)。
马艳芳(1978—),女,博士,副教授,主要从事可信计算、形式化方法等方面的研究;陈亮(1977—),通讯作者,男,博士,副教授,主要从事数值计算等方面的研究。E-mail:clmyf2@163.com
2012-11-12
2013-03-04
1002-8331(2013)11-0015-05
CNKI出版日期:2013-03-15 http://www.cnki.net/kcms/detail/11.2127.TP.20130315.1146.001.html

