接驳地铁系统的公共交通站台线路布置优化研究

崔 愿,陈绍宽*,刘剑锋

(1.北京交通大学城市交通复杂系统理论与技术教育部重点实验室,北京100044；2.北京交通发展研究中心,北京100073)

接驳地铁系统的公共交通站台线路布置优化研究

崔 愿1,陈绍宽*1,刘剑锋2

(1.北京交通大学城市交通复杂系统理论与技术教育部重点实验室,北京100044；2.北京交通发展研究中心,北京100073)

针对接驳地铁的公交线路站台分配不合理现象以及由此引起的公交站台利用率不均衡、服务水平较低等问题,本文以乘客总换乘距离最短、公交排队进站总等待时间最小为目标,使用ε约束方法建立帕累托边界,利用权重系数反映不同决策者对两个目标的偏好,建立接驳地铁系统的公交线路布置优化模型.以北京地铁4号线西苑站接驳地铁的公交系统为例进行案例研究,验证模型有效性与实用性.结果表明:该模型可用于接驳地铁系统的公共交通站台线路布置优化,从而提高公共交通服务水平及公交车辆运行效率.

城市交通;公交线路布置优化;多目标;换乘距离;公交排队等待时间;灵敏度分析

1 引 言

我国城市化水平不断提高,机动车拥有量迅速增加,而交通基础设施仍处于较低水平,道路交通网络承载力面临严峻考验.通过多年的研究与实践,公众逐渐意识到解决我国大城市交通问题的根本出路在于优先发展公共交通.作为大城市公共交通系统骨干的地铁系统,能提供“线到线”的服务,但其效能的充分发挥往往依赖其他交通方式,特别是与地面公交系统的配合与衔接.

目前对于接驳地铁的公交衔接问题的研究成果,主要分为两类.

第一类从公交线路规划和公交站选址方面开展研究.例如,郑毅将与地铁系统接驳的公交线路分为过境线、直接服务区线,研究公共交通的服务区域[1].田启华和陈艳艳确定公交车辆的最佳发车时间及驻站时间,提高枢纽换乘效率及公交运营服务水平[2].Hu等考虑乘客换乘对接驳地铁的公交线路站点布局的影响[3].Quadrifoglio等预测接驳地铁公交线路服务区域的需求密度[4].Ibeasd等基于最小社会成本建立了公交站点最优化的双层模型[5].

第二类是从乘客的换乘行为角度进行研究.例如,姜帆对不同交通方式间的换乘比例及换乘量分布进行了预测[6].姚凤金和杨浩以最短换乘时间为目标,研究换乘枢纽不同时间段的车辆配置数、动态发车时间与动态发车间隔[7].Lo等针对接驳地铁公交车辆的特有策略问题,以缩短乘客换乘等待时间为目标进行研究[8].Guo等通过考虑乘客到达率建立了乘客从轨道交通换乘公交的换乘时间模型[9].Sun等研究枢纽中乘客在不同交通方式之间换乘的概率[10].

总体上看,已有文献对我国大城市接驳地铁的公交车站拥有多个公交站台、公交线路众多等特点的考虑还不够充分,仍有待深入研究；此外,综合考虑乘客换乘特点和公交车辆进站过程的研究成果也有待进一步丰富.

本文以乘客总换乘距离最小、公交排队进站总等待时间最短为目标,同时考虑站台停靠能力,建立接驳地铁系统的公交线路布置双目标优化模型.应用该模型对北京地铁四号线西苑站的公交线路接驳问题进行案例研究,确定不同权重系数下的最优方案集,并对不同目标权重进行灵敏度分析.

2 多目标公交线路优化模型建立

本文针对地铁接驳地面公共交通乘客总换乘距离最小与公交车辆进站总等待时间最短为目标建立优化模型.

2.1 乘客总换乘距离最小

本文将乘客换乘距离定义为从地铁出入口到公交站台的走行距离.与地铁接驳地面公交的换乘过程相比,公交站台内各公交线路间换乘关系十分复杂,且对地铁与地面公交换乘的影响不显著,因此本文暂不考虑.

(1)目标函数.

对于接驳车站,主要考虑地铁和地面公交换乘客流量,乘客总换乘距离计算公式如下.

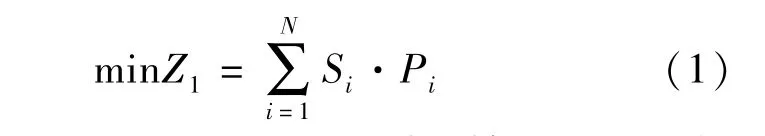
式中 Si——第i个公交站台到地铁出入口的换乘距离；

Pi——第i个公交站台和地铁之间的换乘人数；

N——公交站台总数.本文中线路布置的基本原则是按换乘量大小排序,依次将公交线路分配到距离地铁出入口由近及远、编号为1到N的公交站台,以确保多数换乘乘客的换乘距离最短,地铁出入口和公交站台的相对位置如图1所示.

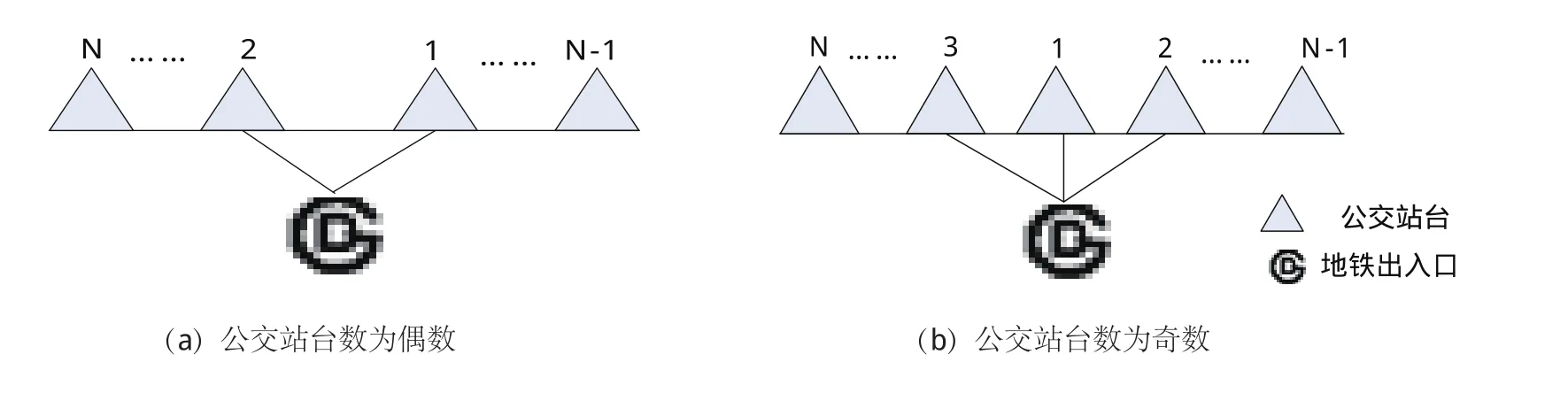
图1 公交站、地铁出入口位置关系Fig.1 Position of the bus stops and the subway entrance

图1所示公交线路布置方式,使乘客换乘距离最短.但将换乘量大、停站时间长的公交线路布置在上游公交站台,上游排队等待进站的公交车辆较多,会阻碍下游站台的公交车辆通过交织区域,如图2(a)所示.假定公交站台1、2、3的乘客换乘量、公交停站时间依次递减,布置顺序如图2(b)所示.

图2 不同公交站台的公交车辆通过交织区域Fig.2 Bus in different bus stops passing weaving sections

图2(a)中下游站台公交车辆通过交织区域受到的影响程度大于图2(b)情况,因此,在后文中考虑建立车辆进站排队模型,以保证车辆排队进站等待时间最小.

(2)约束条件.

站台布置的主要约束条件为公交停靠能力的约束,全部条件如式(2)至式(5)所列.i

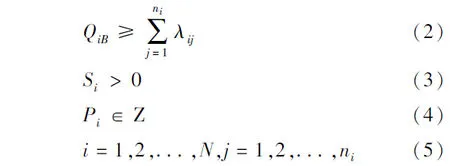
式中 λij——第i个公交站台的第j条公交线路的实际小时到达率；

QiB——第i个公交车停靠站理论通过能力；

ni——每i个公交站台的公交线路数.多泊位公交停靠站的理论通过能力QB的计算公式如下[11]:

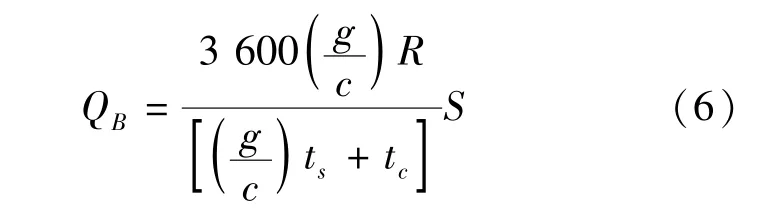
式中 QB——公交车停靠站理论通过能力；

g/c——下游交叉口绿灯时间与该交叉口信号周期之比；

R——由于误点等原因产生的折减系数,按HCM建议取0.833；

ts——乘客上下车时间；

tc——连续两辆公交车的最小车头时距,通常可取5 s[12]；

S——有效泊位数.不同泊位数对应的有效泊位值,如表1所示.

表1 公交停靠站有效泊位数[13,14]Table 1 The actual berths in bus bay and bus stop

2.2 公交车辆排队进站总等待时间最小

本文假设不同站台公交车辆交叉干扰不显著情况下(即因车辆驾驶微观行为差异产生的影响),通过计算每个公交站台的公交车辆排队进站等待时间,累积得到全部公交站台的公交车辆排队进站总等待时间.

(1)目标函数.

考虑到多线路公交停靠站车辆到达服从泊松分布,公交车辆停留时间即站台服务时间服从爱尔朗分布[15],假设每个公交站台的到达车流构成“单路排队多通道服务的M/M/C”模型,排队规则为先到先服务(FCFS),其中C为公交泊位数.

第i个公交站台的公交车辆平均到达率为

设Bij为第i个公交站台第j个公交线路的乘客平均上下车时间,单位为s,则第i个公交站台乘客平均上下车时间为

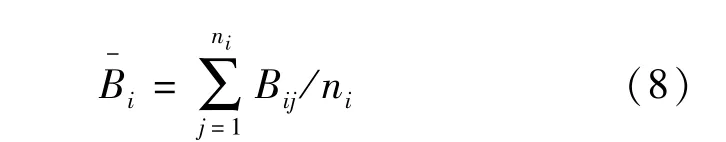
第i个公交站台每小时服务的车辆数,即平均

服务率为

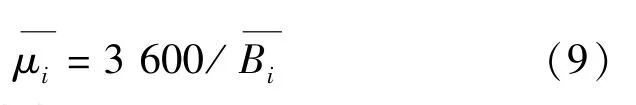
根据排队论有如下计算公式.

第i个公交站台的服务强度为

第i个公交站台没有车排队的概率为

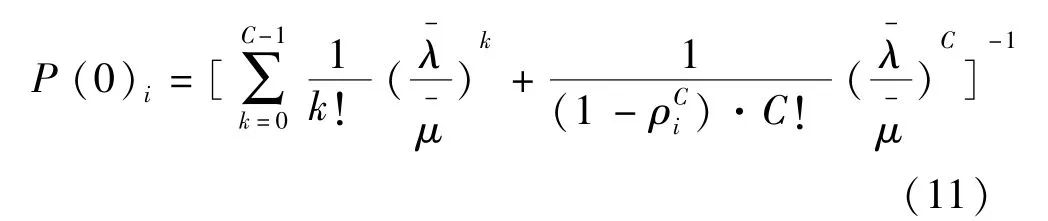
第i个公交站台排队公交的平均队长为

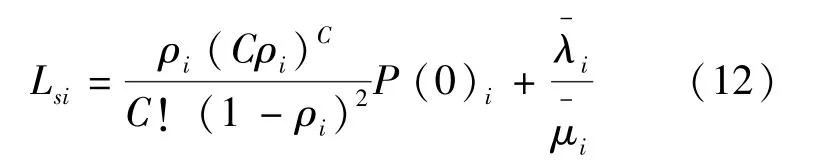
第i个公交站台排队公交的平均等待时间为

全部公交车辆的总等待时间即目标函数为

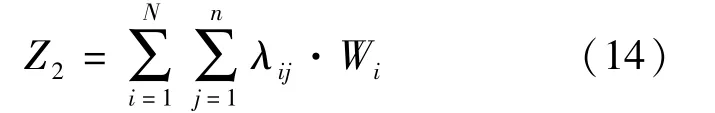
(2)约束条件.

约束条件表示只有当第i个公交站台的服务强度ρi＜1时,第i个站台的公交车数不会排成无限的队列,到站公交车辆能够逐步消散.

3 多目标模型优化求解

本文针对建立的多目标优化模型,通过构建Pareto边界将多目标问题转化为单目标问题,以获得优化模型的解.

第1步构建Pareto边界.

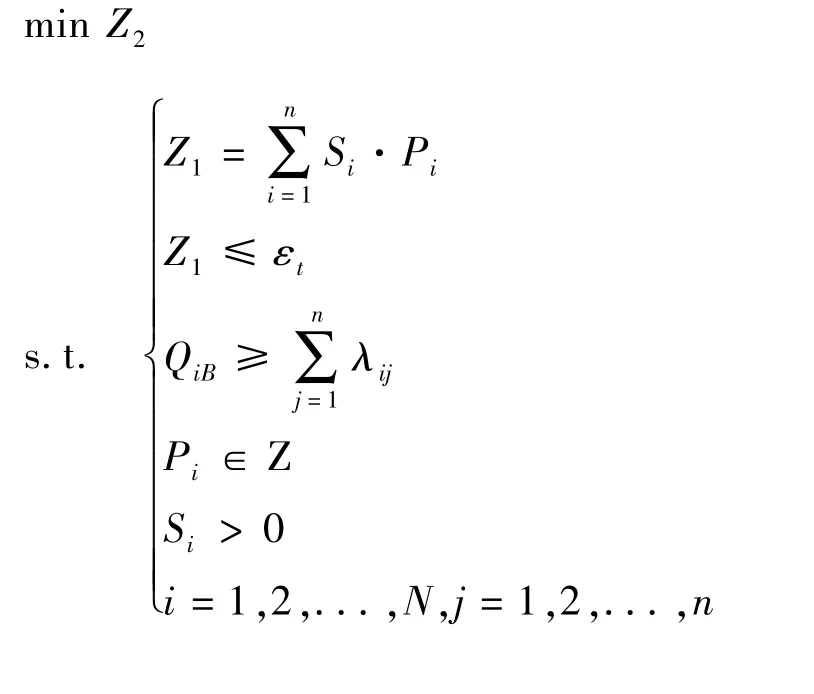
使用ε约束方法,选择Z2作为主要优化目标,将Z1作为约束条件之一,从而将多目标问题转化为单目标优化问题,转化后模型如下.其中,εt是第一个目标函数的上界.通过给出适当εt的值,将第一个目标函数的值划分为一系列间距相等的子区间进行求解.图3阐述了ε约束方法,在一个假定方案上进行选择.通过调整系统的εt作为Z1的值,可搜索到更多最优解,这些最优解的点(Z1,Z2)构成了原始Pareto边界.

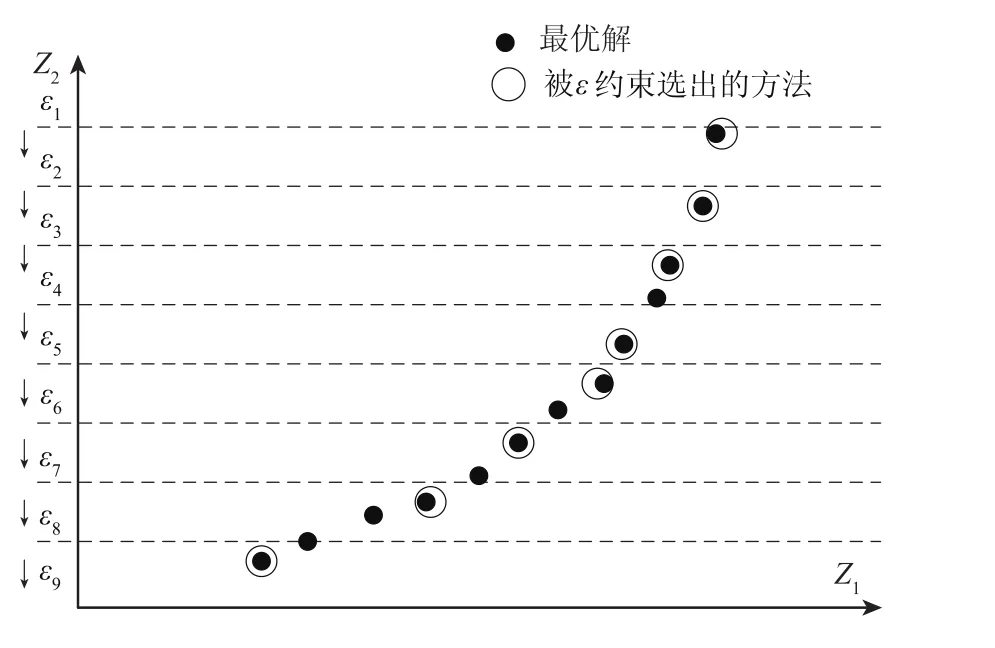
图3 ε约束方法[16]Fig.3 Illustration of the ε constraint approach

第2步多目标分析.

换乘距离与等待时间的单位不相同,两个目标值不能直接比较或叠加,需将其标准化,计算公式如下:

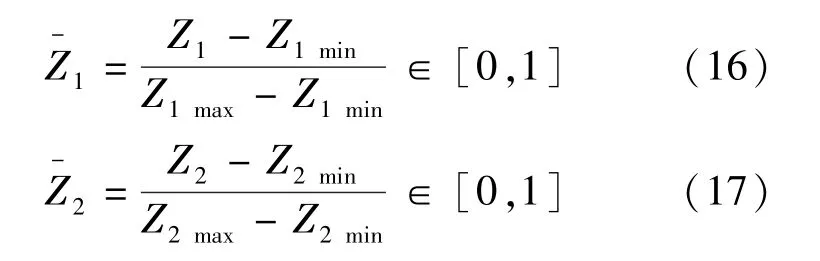
最理想的点为(0,0),最差的点为(1,1),使用基于距离的方法从备选方案中找到最优解.

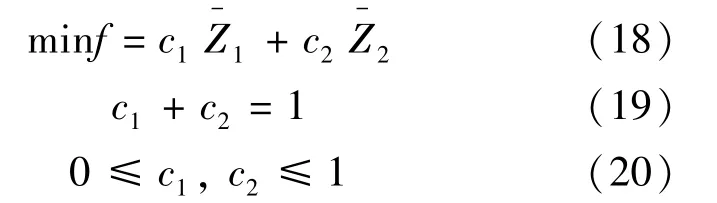
式中 c1和c2——两个目标的权重系数,反映决策者的偏好,权重系数越接近1表示该目标函数越重要.

4 案例研究

以北京地铁四号线西苑站接驳公交线路为例,进行案例研究,验证上述模型的有效性.

4.1 现状分析

北京地铁四号线西苑站位于西北四环外,距颐和园小学、颐和园、香山景点较近.由于四号线地铁未覆盖香山、温泉、永丰、马连洼等地区,西苑站连接市区和西北郊区,工作日的通勤客流及节假日去往景点的旅游客流较多,换乘需求较大.

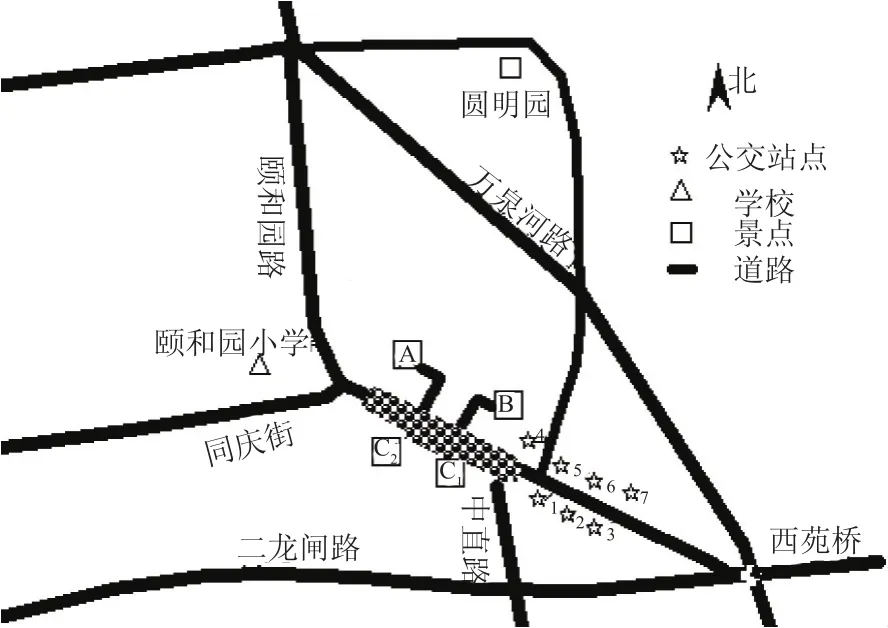
图4 西苑站周边交通图Fig.4 Traffic around the Xiyuan subway station

地铁西苑站周边道路及公交站点情况如图4所示.地铁西苑站有四个出入口,A、B口位于西苑交通枢纽内,C1、C2口位于同庆街及中直路交叉口之间.三个公交站台位于地铁C1口东侧,18条公交线路在此停靠,该停靠站共有6个港湾式泊位,调查数据如表2所示.

下游的交叉口距离公交车站比较远,绿信比g/c取1.通过计算,当前站台方案的实际乘客总换乘距离为241 958 km,公交车进站总等待时间为89 min,换乘乘客的换乘距离过长.在公交站点1停靠的公交线路仅有3条,泊位利用率低,泊位没有得到充分利用.在站点2、站点3停靠进站的公交线路达6条和9条,泊位利用率较高,但公交车排队等待进站的问题较严重.

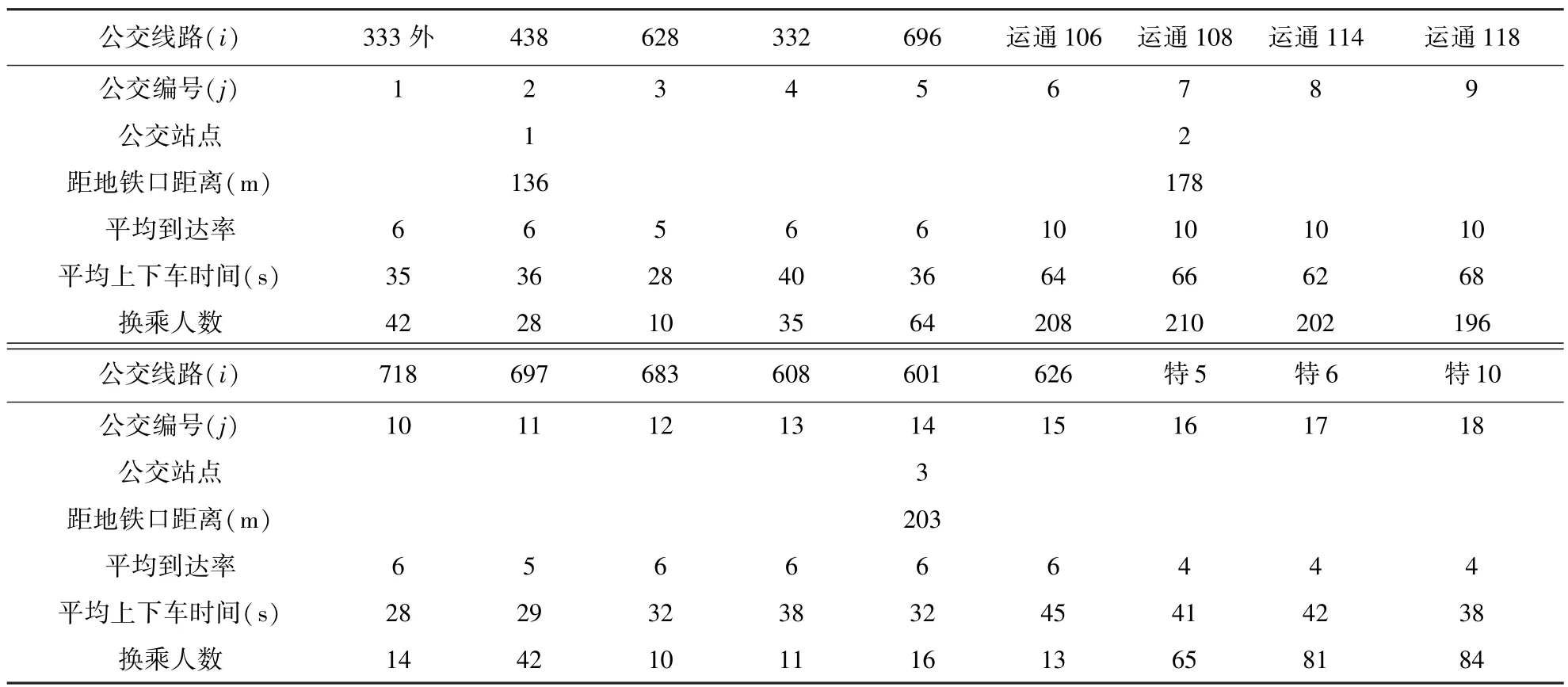
表2 模型测量数据Table 2 Survey data for model

4.2 线路布置方案

本文假设公交站台上公交线路均匀布置,站台1、站台2、站台3各设置6条公交线路.将公交线路按乘降量从大到小、由近及远布置到公交站台上,最小总换乘距离Z1min为197.57 km,此时公交进站最长等待时间Z2max为93.62 min.公交排队总等待时间随乘客换乘距离增加而减小,考虑到当乘客距离增加到225.38 km时,公交排队进站总等待时间为85.61 min,不再随着换乘距离的增加而减小,因此,后文分析中忽略总换乘距离大于225.38 km的方案,取最大总换乘距离Z1max为225.38 km,公交排队进站最短等待时间Z2min为85.61 min.

利用lingo软件,使用ε约束方法获得137个最优解,构成原始的Pareto边界,如图5所示.

取最优点和最差点分别是(Z1min=197.57, Z2min=85.61)和(Z1max=225.38,Z2max=93.62),标准化公式如下.

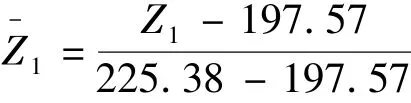
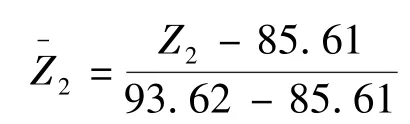
式中 Z1——乘客总换乘距离函数；

Z2——公交进站总等待时间函数.基于标准化公式,标准化后的Pareto边界如图6所示.

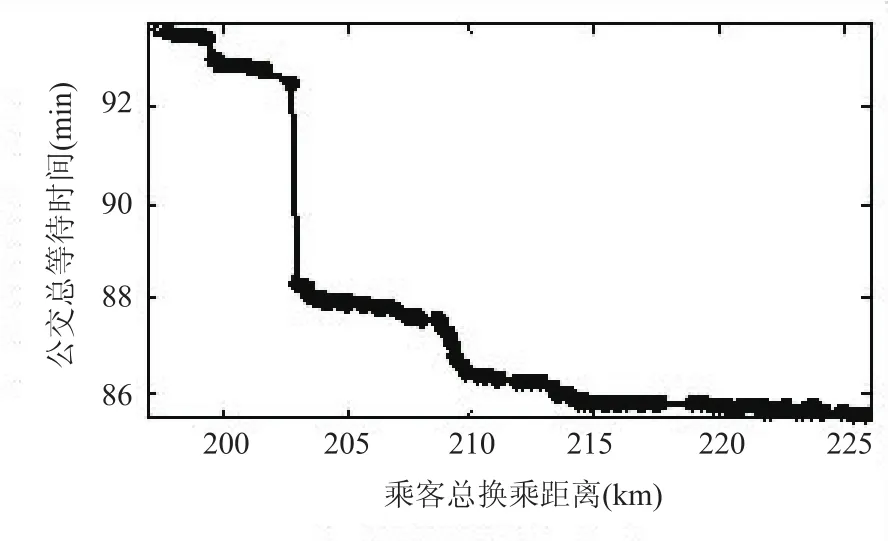
图5 原始帕累托边界Fig.5 Original Pareto frontier

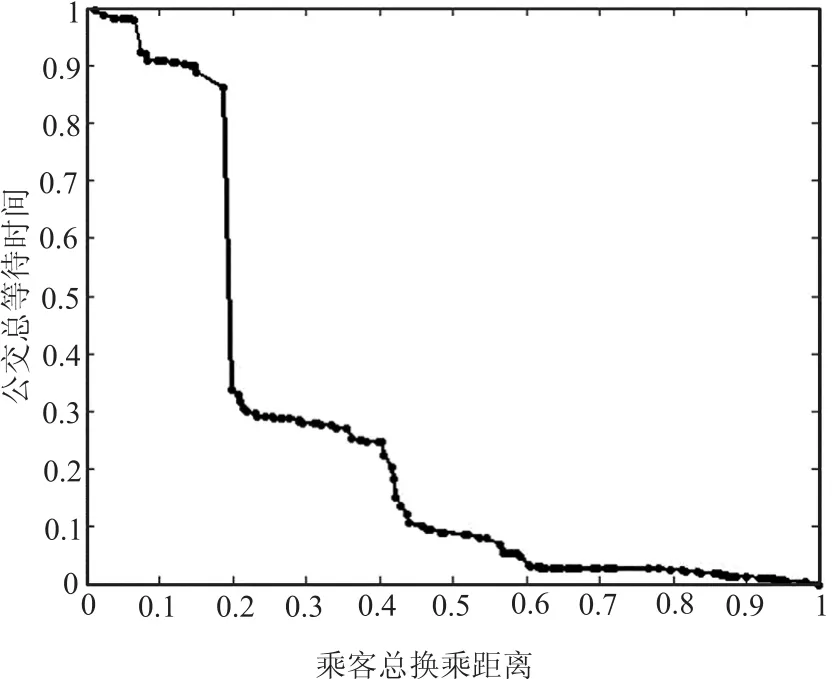
图6 标准化帕累托边界Fig.6 Normalized Pareto frontier

目标函数权重系数会影响方案的优劣性及最优方案的确定,不同权重系数下最优方案及优化率如表3所示.

如表3所示,c1逐渐增大,c2逐渐减小,不同权重下最优方案的距离优化率变大,公交排队时间优化率变小.当决策者重视乘客换乘距离,将换乘量大的公交线路集中分配到靠近地铁口公交站台上,则此泊位进站停车的公交车排队等待时间将显著增加.

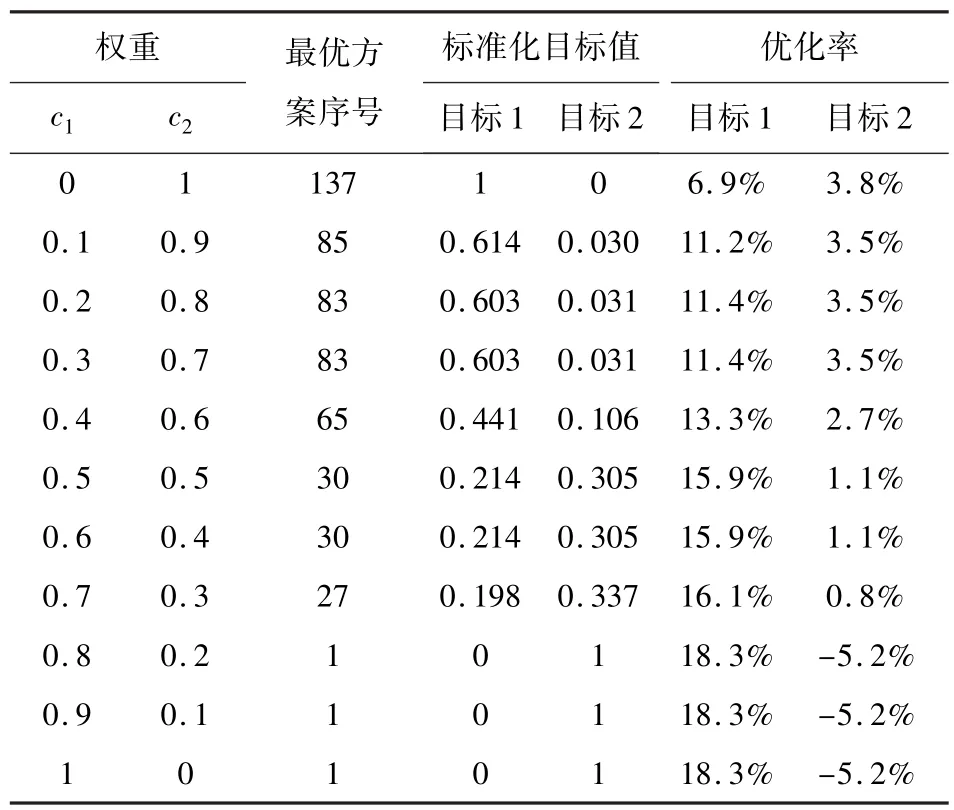
表3 不同权重下多目标最优解及优化率Table 3 Optimal solution and optimization rate under different coefficients

4.3 灵敏度分析

对目标权重系数进行灵敏度分析,反映决策者对换乘距离与等待时间的偏好差异.不同权重下的方案目标值曲线如图7所示,其中系列1为c1=0, c2=1；系列2为c1=0.1,c2=0.9,依此类推,系列11为c1=1,c2=0.

由图7可知,部分方案对权重变化较敏感.例如,方案1至26,方案64至137,不同权重系数下总目标值的标准差在0.1到0.3之间.这些方案分目标标准值相差较大,例如方案12,把编号为6、7、8、9、11、18的公交线路布置在1站台,编号1、3、4、5、16、17的线路布置在2站台,编号2、10、12、13、14、15的线路布置在3站台时,分目标的标准值分别为0.075和0.923,不同权重系数下的总目标值相差较大.

部分方案对权重系数变化不敏感,例如,方案27至63,不同权重系数下总目标值的标准差在0到0.1之间.这些方案分目标标准值较接近,例如方案42,把编号为6、7、8、11、16、18的公交线路布置在1站台,编号1、3、5、9、14、17的线路布置在2站台,编号2、4、10、12、13、15线路布置在3站台时,分目标的标准值分别为0.29和0.28,不同权重系数下的总目标值相差较小.

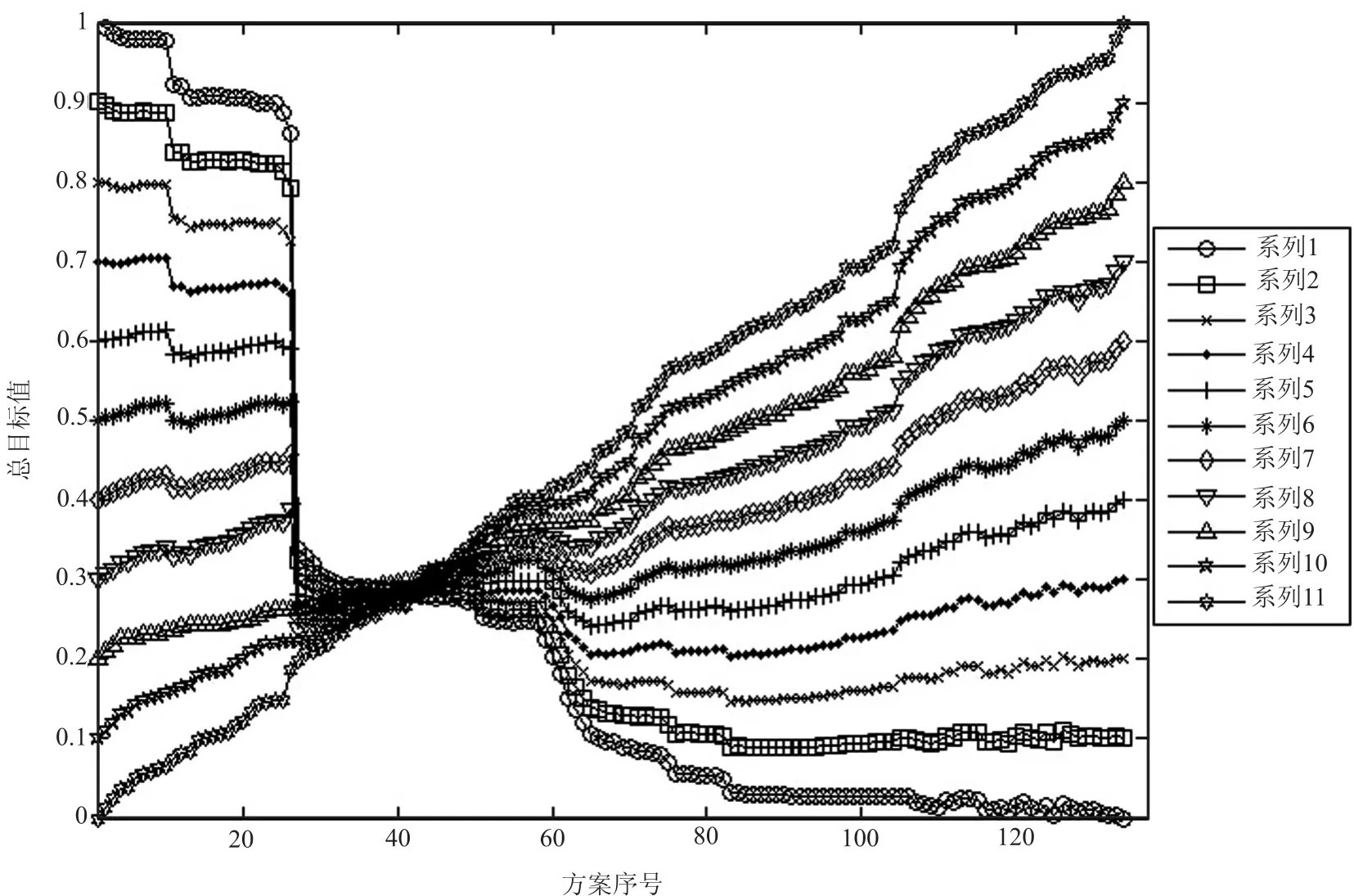
图7 备选方案随权重变化图Fig.7 Variations of alternatives with coefficient

5 研究结论

本文以接驳地铁系统的公交站台线路布置优化问题为研究对象,以所有乘客换乘距离最短、公交总排队进站等待时间最小为目标,建立了多目标优化模型.结合案例研究,得到以下结论.

(1)本文结合乘客换乘距离和公交进站等待时间构建模型,考虑两方面对换乘效率及服务水平的影响.缩短乘客换乘距离,有利于提高换乘服务水平与效率,吸引更多的人选择公共交通出行；减少公交进站时间,有助于减少乘客途中时间,提高公交运营公司的收益.

(2)本文使用ε约束方法将多目标问题转化为单目标问题,利用权重系数反映不同决策者对两个目标的偏好.

(3)以北京地铁四号线西苑站接驳公交线路为例,验证模型的有效性.结果表明,所建模型适用于现有公交线路布置优化问题,通过对所得137个方案进行灵敏度分析,可知不同方案对权重系数变化的反应存在一定差异.

[1] 郑毅.北京市轨道交通乘客出行方式选择分析[J].交通运输系统工程与信息,2011,11(3):163-168.[ZHENG Y.Analysis on passenger trip mode split of Beijing subway[J].Journal of Transportation Systems EngineeringandInformationTechnology, 2011,11(3):163-168.]

[2] 田启华,陈艳艳.区域公交协调调度优化算法研究[J].交通运输系统工程与信息,2011,11(4):160-165.[TIANQH,CHENYY.Coordinated scheduling optimization for public transport hub[J]. Journal of Transportation Systems Engineering and Information Technology,2011,11(4):160-165.]

[3] HuYu-cong,Zhang Qi,Wang Wei-ping.A model layout region optimization for feeder buses of rail transit[J].Procedia-Social and Behavioral Sciences, 2012,43:773-780

[4] Luca Quadrifoglio,Xiugang Li.A methodology to derive the critical demand density for designing and operating feeder transit services[J].Transportation Research Part B,2009,43(10):922-935.

[5] Ángel Ibeas,Luigi dell'Olio,Borja Alonso,et al. Optimizing bus stop spacing in urban areas[J]. Transportation ResearchPartE,2010,46(3): 446-458.

[6] 姜帆.关于轨道交通需求预测与城市客运交通枢纽关系的研究[J].交通运输系统工程与信息,2001, 1(4):311-315.[JIANG F.Study on the relation of rail trafficdemandwithurbanpassengertransitjunction[J].JournalofTransportationSystems Engineering and Information Technology,2001,1(4): 311-315.]

[7] 姚凤金,杨浩.旅客枢纽换乘时间调度研究[J].交通运输系统工程与信息,2008,8(1):133-137. [YAO F J,YANG H.On transferring time scheduling of passenger hubs[J].Journal of Transportation Systems EngineeringandInformationTechnology, 2008,8(1):133-137.]

[8] Shih-Che Lo,Wei-Jea Chang.Design of real-time fuzzy bus holding system for the mass rapid transit transfer system[J].Expert System With Applications,2012, 39(2):1718-1724.

[9] GuoShu-xia,Lei Yu,Chen Xu-mei,et al.Modelling waiting time for passengers transferring from rail to buses[J].Transportation Planning and Technology, 2011,34(8):795-809.

[10] SunLi-shan,Rong Jian,Yao Li-ya,et al.Entropy-based estimationoftransfersinaterminal[J]. Transportation Planning and Technology,2012,35(3): 305-315.

[11] 任福田,等译.美国道路通行能力手册[M].中国建筑工业出版社,1991:488-567.[REN F T,et al. The American road capacity manual[M].China Building Industry Press,1991:488-567.]

[12] Paulo Silva.Simulating bus stops in mixed traffic[J]. Traffic Engineering and Control.,2000,41(4): 160-167.

[13] Herbert S,Levinson.Analyzing transit travel time performance [J].Transportation Research Record,1983:1-6.

[14] Herbert S,Levinson.Bus lane capacity revisited[J]. Transportation Research Record1664,1998.

[15] 邵俊.公共汽车交通专用道(路)系统设计与评价方法研究[D].同济大学,2000.[SHAO J.Research on bus transit lane system design and evaluation method[D].Tongji University,2000.]

[16] Banu Soylun,Selda Kapan Ulusoy.A preference ordered classification for a multi-objective max-min redundancy allocation problem[J].Computers&Operation Research.,2011,38(12): 1855-1866.

Layout Optimization of the Feeder Bus Routes Connecting Subways at Bus Stops

CUI Yuan1,CHEN Shao-kuan1,LIU Jian-feng2
(1.MOE Key Laboratory for Urban Transportation Complex Systems Theory and Technology, Beijing Jiaotong University,Beijing 100044,China；2.Beijing Transportation Research Center,Beijing 100073)

Aiming at unreasonable distribution of feeder bus lines which leads to unbalanced utilization rate of bus stops and the low level of passenger service,an optimization model is established to obtain the shortest total passenger's transfer distance and the minimum the total time of all buses dwelling at bus stops.This paper gives Pareto frontiers by constraint approach and employs weight coefficients to indicate the preference of decision makers.Case studies of the Xiyuan Station in Beijing are implemented to verify the validity and practicability.The results from case studies shows that the proposed model is capable of optimizing the layout of the feeder bus routes connecting subways at bus stops and improving the level of public transit service and the operational efficiency of buses.

urban traffic；optimization layout of the feeder bus routes；multi-objective；transfer distance；queuing and waiting time；sensitivity analysis

U121

A

U121

A

1009-6744(2013)06-0176-08

2013-05-06

2013-08-01录用日期:2013-09-23

国家重点基础研究发展计划(973计划)(2012CB725406)；国家自然科学基金项目(71001006,71131001).

崔愿(1988-),男,北京人,硕士生.

*通信作者:shkchen@bjtu.edu.cn