基于生态位理论的航运产业集群竞争研究

金嘉晨,真 虹

(1.上海海事大学物流研究中心,上海201306；2.上海国际航运研究中心,上海200082)

基于生态位理论的航运产业集群竞争研究

金嘉晨1,2,真 虹*2

(1.上海海事大学物流研究中心,上海201306；2.上海国际航运研究中心,上海200082)

为研究航运产业集群之间的生态关系,在结合航运产业集群发展实际和发展特点的基础上,利用生态学中有关物种关系的理论模型,提出航运产业集群竞争关系、互利关系和支配关系的理论模型,给出三种群间关系的生态均衡条件;借助正向、反向和优势比较等生态位重叠度测算方法,对上海和宁波航运产业集群的生态竞争关系进行实证分析,得出上海和宁波航运产业集群在集装箱货运发展方面的生态相似性极高,竞争极为激烈,并且上海航运产业集群具有更强的生态位竞争优势,提出上海和宁波航运产业集群必须加快实现“错位竞争、优势互补”的发展格局.

交通运输经济;竞争;生态位重叠;航运产业集群;生态

1 引 言

产业集群是指在某一特定领域内互相联系的、在地理位置上集中的公司和机构集合[1].由于产业集群与生态系统中的生物种群之间存在着天然相似的特征,将生态学的有关理论引入产业经济领域已经得到越来越多的重视.仇保兴提出,集群内的每一个企业都要找到自己的“生态位”才能保持集群的稳定[2].这一提法为学界分析产业集群的生态平衡提供了研究思路.

当前我国沿海沿江城市在发展航运产业集群的过程中面临着如何有效利用航运资源,如何处理相互关系等问题.但国内外对航运产业集群的研究还集中在航运产业集群的内涵构成[3]、发展模式[4]、竞争力[5]等,对揭示航运产业集群之间的相互关系鲜有涉及.本文利用生态学中研究物种相互关系的理论模型,对航运产业集群的生态关系进行梳理,借助生态位理论的有关原理和方法对航运产业集群的群间竞争进行实证分析,为我国航运产业集群发展深化资源配置、协调相互关系提供依据,对引导我国航运产业集群走向生态平衡具有现实意义.

2 航运产业集群的生态关系

从世界各国航运产业集群的发展可以看出,尽管各地航运产业集群的构成要素不尽相同,但是基本功能大多具备.对于不同的航运产业集群而言,其相互间的关系主要包括竞争关系、互利关系和支配关系.

2.1 航运产业集群的竞争关系

不同航运产业集群利用同一短缺资源时,集群之间就会产生竞争,并且每个集群的存在都会对其他集群的发展产生抑制作用.以同区域内只有甲、乙两个航运产业集群的情形为例,在不考虑甲乙之间竞争关系的情况下,甲、乙的集群规模符合逻辑斯谛增长方程,分别为

式中 N1、N2代表甲、乙航运产业集群的集群规模,r1、r2代表在理想状态下甲、乙航运产业集群的规模增长率,K1、K2表示甲、乙航运产业集群在所处环境下所能达到的规模上限.

由于甲、乙航运产业集群之间存在竞争关系,在此引入竞争系数(competition coefficients)来表示两者的竞争程度.α12是乙的竞争系数,α12·N2表示乙对甲的竞争抑制作用；同样的,α21是甲的竞争系数,α21·N1表示甲对乙的竞争抑制作用.考虑了甲、乙竞争关系后的竞争方程为[6]

显然,要实现甲、乙集群竞争的平衡状态,就必须同时满足d N1/dt=0和d N2/dt=0.可以得到,此时的甲、乙航运产业集群的集群规模分别为

根据K1、K2、α12和α21的取值不同,甲、乙航运产业集群将达到两种不同结果的平衡状态.若N1=0,N2=K2或N2=0,N1=K1,即甲、乙的其中一方将被另一方完全取代的情况,甲、乙航运产业集群将达到不稳定的平衡状态,甲或乙均能抑制对方发展.若同时满足K1＜K2/α21和K2＜K1/α12,即当K1=K2时,α21和α12必须小于1；当K1≠K2时,同时满足α12α21＜1和K1/K2的比值处于α12～1/α21之间,即任何一个集群的规模都不足以排除另一集群的情况,甲、乙航运产业集群将达到稳定的平衡状态,竞争双方仍然可以共存.两种平衡状态的均衡条件表示,具有竞争关系的航运产业集群,只有实现错位发展才能避免因同质竞争造成的集群被取代.

2.2 航运产业集群的互利关系

不同航运产业集群的发展对彼此都有促进作用时,集群之间存在互利关系.同样地,以只有甲、乙两个航运产业集群的情形为例,在不考虑甲乙之间互利关系的情况下,甲、乙的集群规模符合逻辑斯谛增长方程,分别为

式中 N1、N2代表甲、乙航运产业集群的集群规模；r1、r2代表在理想状态下甲、乙航运产业集群的规模增长率；K1、K2表示甲、乙航运产业集群在所处环境下所能达到的规模上限.

由于甲、乙两个航运产业集群之间存在着互利关系,在此引入互利系数来表示两者对彼此的促进作用.β12是乙的互利系数,β12·N2表示乙对甲的促进作用；同样的,β21是甲的互利系数,β21·N1表示甲对乙的促进作用.因此,考虑了甲、乙互利关系后的竞争方程为

甲、乙航运产业集群达到均衡状态的条件是,同时满足dN1/dt=0和dN2/dt=0.可以得到,此时的甲、乙航运产业集群的集群规模分别为

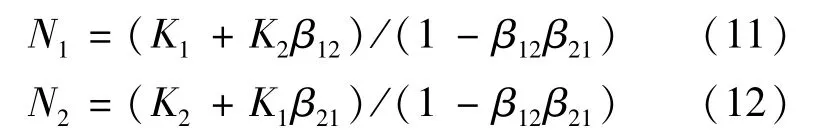
由于N1和N2均大于0,因此(1-β12β21)必然也大于0.从而得到β12β21＜1是使甲、乙航运产业集群实现互利的均衡条件.达到均衡条件存在两种情况,一种为β12和β21均小于1,另一种为β12和β21中有一个大于1,一个小于1.均衡的意义表示,具有互利关系的航运产业集群,其各自的发展仍然需要保持一定的独立性.

2.3 航运产业集群的支配关系

不同航运产业集群的集群规模和集群竞争力相差较大,强势的一方往往占据发展的支配权和主导权,弱势的一方往往处于从属和被支配的地位,形成中心-卫星式的航运产业集群关系模式.航运产业集群与集群之间的支配从属关系类似于生态学中的捕食者与被捕食者的关系.考虑“一中心,一卫星”的单模式情形,中心集群和卫星集群处于同一生态空间内.对于中心集群,假定卫星集群不存在的情况下,其集群规模增长为

式中 N1代表中心集群的集群规模；r1代表在理想状态下中心集群的规模增长率；K代表生态空间内所能容纳的最大集群规模；如果卫星集群存在,中心集群的规模发展会因为受到卫星集群对发展资源的分享而有所减缓.这种减缓可以用新的方程表达:

式中 ω表示卫星集群的资源利用系数；ωN2表示由于卫星集群成长造成有限资源的分散化对中心集群的发展所产生的影响.对于卫星集群,如果中心集群不存在,卫星集群的发展会因为缺乏中心集群的引导和支撑,其集群规模出现萎缩,卫星集群的集群规模萎缩方程为[7]

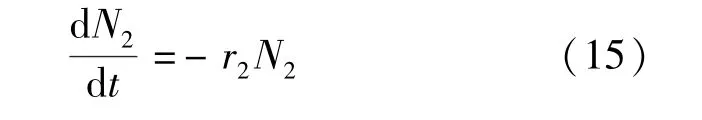
式中 N2代表卫星集群的集群规模；r2代表中心集群不存在时卫星集群规模的萎缩率.如果中心集群存在,卫星集群的规模发展会因为受到中心集群的支配和引导而有所增长.这种增长可以用新的方程表达:

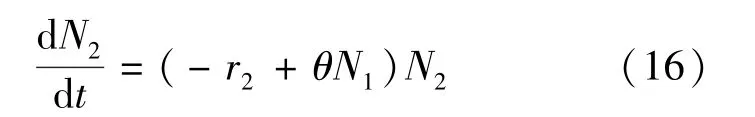
式中 θ表示中心集群的支配系数；θN1表示中心集群为卫星集群提供的发展支撑.

显然,使得中心集群和卫星集群达到均衡状态的条件是,同时满足dN1/dt=0和dN2/dt=0.可以得到,此时的中心集群和卫星集群的集群规模分别为

并且,由于K代表生态空间内所能容纳的最大集群规模,因此存在K-N1≥0,即K≥r2/θ.均衡时的意义表示,卫星集群规模的萎缩率必须小于等于中心集群的支配系数与最大集群规模的乘积.也就是说,在航运产业集群的群间支配关系中,中心集群必须对卫星集群有足够的影响力和支配力,才能够达到均衡状态,并对两者的发展都起到促进作用.

3 航运产业集群的生态竞争测度方法

在航运产业集群的各种生态关系中,竞争关系是最为常见也是最为重要的关系.由于航运产业集群发展所需的资源往往是有限的,为了获取资源,处于同一环境的不同航运产业集群之间就不可避免地产生竞争.对竞争关系的测度是促进航运产业集群实现生态平衡的关键环节.

现代生态学中的生态位理论是用来表征生物单位(个体、种群或物种)对资源利用状况的重要概念,可以间接反映生物单位之间的竞争情况.生态位是指一个生物单位生存条件的总集合体,当不同的生物单位利用同一资源或共同占有其他环境变量时,就会出现生态位重叠现象.本文借助对称生态位重叠测算法和非对称生态位重叠测算法,从正向、反向和优势比较等方面对多个航运产业集群对同一资源的共同利用程度进行测度.

3.1 对称生态位重叠测算法

对称生态位重叠测算法主要有Pianka法、简化Morisita法、Horn法和Levins法[8]. Pianka法表示为

简化Morisita法是在非个体计数情况下,对Morisita法进行简化的结果,表示为

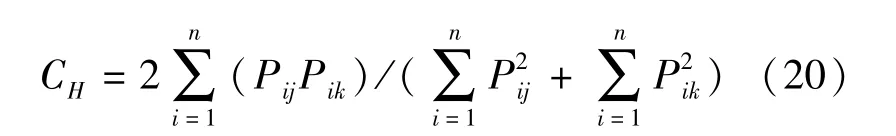
Horn法是一种信息论方法,表示为

上述式中,j与k分别代表两个物种,i代表生态位所使用的资源种类,Pij与Pik分别为物种j与物种k在总资源中使用资源种类i的比例,n为资源种类数.Ojk、CH和R0都介于0和1之间.数值越大,表明物种之间的生态位重叠度越严重；当数值为1时,两个物种之间的生态位完全重叠；当数值为0时,两个物种之间的生态位完全分离.

Levins法测度的是不同物种之间生态位的空间距离,是从反向揭示不同物种之间的生态位重叠程度.Levins法的公式为

式中 Ojk为物种j与物种k之间的Levins生态位重叠度,0≪Ojk≪1,Ojk越小,表明物种j和物种k之间的生态位重叠度越严重；当Ojk=0时,两个物种占据完全相同的生态空间,其资源利用的模式完全相同,生态位完全重叠；当Ojk=1时,两个物种之间的生态空间非常大,使用完全不同的资源,生态位完全分离.

3.2 非对称生态位重叠测算法

前述方法从正向和反向描述了不同物种之间的生态位重叠程度,但是只能反映不同物种对资源利用的相似性和竞争状况.由于MacArthur-Levins法的公式是非对称的,可以借此考察不同物种在资源利用上哪一方更具有竞争优势,便于研究者对不同物种之间可能出现的竞争排斥或替代进行预判.不对称α法的具体公式为[9]

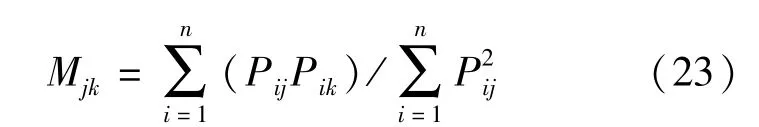
式中 Mjk是指以物种j的资源使用为基准,物种k对物种j的生态位重叠度(或生态位竞争优势值). Pij与Pik分别为物种j与物种k在总资源中使用资源种类i的比例,n为资源种类数.

4 航运产业集群的生态竞争实证分析

航运企业和港口企业是航运产业集群的重要组成部分.不同航运产业集群的航运企业和港口企业在资源利用方面的状况能在一定程度上反映两者之间的竞争关系.集装箱吞吐量是恰能同时反映航运企业和港口企业资源利用绩效的重要指标.因此,本文选取集装箱吞吐量作为测算航运产业集群之间生态位竞争的指标参数.

上海、宁波是我国航运产业的发达地区.同扼长三角经济区的地理区位为上海、宁波发展航运产业提供了得天独厚的自然优势,但是也造成上海、宁波对腹地资源的激烈竞争.及时、有效地对两地航运产业集群的竞争关系加以界定十分必要.

根据航线的不同,可以将上海、宁波航运产业集群的集装箱货运资源分为国际航线、国内航线和内支线三个资源维度,如表1所示.

本文利用式(19)、式(20)、式(21)和式(22)从正向和反向两个方面,就集装箱货运资源维度对上海、宁波航运产业集群的生态位重叠度进行计算,如表2所示.结果显示,2005年至2011年,上海和宁波航运产业集群的生态位重叠度非常高,正向指标基本都达到97%及以上的高位,反向指标则处于2.3%左右.意味着两个航运产业集群在集装箱货运发展方面的生态相似性极高,两者对集装箱货运资源的利用模式非常相似,生态竞争非常激烈.但值得可喜的是,上海和宁波航运产业集群的生态位重叠度出现逐步弱化的趋势.无论是正向指标还是反向指标,都出现了一个百分点的生态位分离.

表1 2005-2011年上海和宁波集装箱吞吐量数据Table 1 2005-2011 Shanghai and Ningbo container throughput

表2 上海和宁波航运产业集群的生态位重叠度Table 2 Niche overlap of Shanghai and Ningbo maritime cluster

借助式(23),对上海和宁波航运产业集群的资源利用能力进一步做比较.结果显示,M上海,宁波的取值均大于1,M宁波,上海的取值则都低于0.9,说明相对于宁波航运产业集群,上海航运产业集群对集装箱货运资源的利用能力更强,其具备的生态位竞争优势更大.并且上海航运产业集群对宁波航运产业集群的生态位竞争优势有增强的趋势.

表3 上海和宁波航运产业集群的生态位竞争优势比较Table 3 Comparison of niche competitive advantage of Shanghai and Ningbo maritime cluster

因此,上海和宁波航运产业集群的生态竞争关系如图1所示,即上海和宁波航运产业集群的大部分生态位空间为两个集群共有,其余为各自分别占有.此时两个集群可以实现共存,但是由于上海航运产业集群具有较强的竞争优势,可能出现占有宁波航运产业集群生态位空间的重叠部分.并且,从上海集装箱货运量增速放缓的事实来看,现有发展空间已经无法长期支撑两个航运产业集群的规模发展.而上海和宁波航运产业集群的生态位分离速度和分离程度仍不明显,亟需从建设东部航运经济高地、打造世界级航运产业集群的战略高度出发,加快上海和宁波航运产业集群错位发展的战略步伐.

图1 上海和宁波航运产业集群的生态竞争关系Fig.1 Ecological competition relation between Shanghai and Ningbo maritime cluster

5 研究结论

本文根据航运产业集群的发展实际,将航运产业集群之间的相互关系表示为竞争关系、互利关系和支配关系.类比生态学中描述物种之间竞争、互利和捕食关系的理论模型,给出适用于航运产业集群生态关系的理论模型,得出具有竞争关系的航运产业集群,要通过错位发展以避免因同质竞争造成的集群被取代；具有互利关系的航运产业集群,其各自发展仍要保持一定的独立性；具有支配关系的航运产业集群,中心集群必须对卫星集群有足够的影响力和支配力.利用生态位重叠度测算方法,对上海和宁波航运产业集群的生态竞争进行实证分析,得出两个航运产业集群在集装箱货运发展方面的生态相似性极高,并且上海航运产业集群具有更强的生态位竞争优势,提出上海和宁波航运产业集群必须加快实现“错位竞争、优势互补”的发展格局.

[1] Porter,M.E.Competitive Strategy[M].Free Press, New York,1980.

[2] 仇保兴.小企业集群研究[M].上海:复旦大学出版社,1999.[CHOU B X.Research on cluster of small businesses[M].Shanghai:Fudan University Press, 1999.]

[3] FISHER ASSOCIATES.The future of London's maritime services cluster:A call for action[R].London,2004.

[4] 宋炳良.上海航运产业集群发展模式及相应对策[J].水运管理,2007,29(5):5-13.[SONG B L. Group development mode and its related strategy for shippingindustryinShanghai[J].Shipping Management,2007,29(5):5-13.]

[5] 陈继红,真虹.基于灰色关联的航运产业集群竞争力评价与应用[J].交通运输系统工程与信息,2009,9 (5):110-116.[CHEN J H,ZHEN H.Evaluation and applicationonshippinglndustrycluster's competitiveness usinggrayrelationaltheory[J]. Journal ofTransportationSystemsEngineeringand Information Technology,2009,9(5):110-116.]

[6] 尚玉昌编著.普通生态学[M].北京:北京大学出版社,2010:175-186.[SHANG Y C.General Ecology [M].Beijing:Beijing University Press,2010:175-186.]

[7] 杨效文,马继盛.生态位有关术语的定义及计算公式评述[J].生态学杂志,1992,11(2):44-49.[YANG X W,MA J S.A review on some terms related to niche and theirmeasurements[J].ChineseJournalof Ecology,1992,11(2):44-49.]

[8] 张文军编著.生态学研究方法[M].广州:中山大学出版社,2007:108-110.[ZHANG W J.Methodology on ecology research[M].Guangzhou:Zhongshan University Press,2007:108-110.]

Research on the Maritime Cluster Competition Based on Ecological Niche Theory

JIN Jia-chen1,2,ZHEN Hong2
(1.Logistics Research Center,Shanghai Maritime University,Shanghai 201306,China；2.Shanghai international shipping institute,Shanghai 200082,China)

In order to study the relations between maritime clusters,by using the theoretical models about the relationship between species in ecology,competition relation,mutually beneficial relation and dominance relation is considered as chief relations on the basis of facts and characteristics of maritime cluster.And three theory models of maritime cluster with ecological equilibrium condition are also given.With forward,reverse and comparative niche overlap methods,a case study of ecological competition between Shanghai and Ningbo maritime cluster is carried out,making it clear that Shanghai and Ningbo maritime cluster has high overlap in container development,and Shanghai has stronger competitive advantages,considering Shanghai and Ningbo maritime cluster must speed up the realization of“dislocation competition,complementary advantages”.

transportation economy；competition；niche overlap；maritime cluster；ecology

U692

A

U692

A

1009-6744(2013)06-0032-05

2013-05-20

2013-07-09录用日期:2013-07-17

上海高校知识服务平台建设项目(ZF1209).

金嘉晨(1985-),女,江苏无锡市人,博士生.

*通讯作者:shzhenhong@gmail.com