数值建模方法对混凝土靶板侵彻过程的影响

邓勇军，姚 勇，王汝恒，周 晶，陈代果，李顺美

(西南科技大学土木工程与建筑学院，四川绵阳 621000)

自20世纪70年代开始，靶板侵彻问题一直备受众多学者的关注。混凝土作为当前军事建筑物、交通要道及其他防护工程的主要建造材料，国内外研究者对其侵彻方面的问题做了大量的研究，也取得了相应的研究成果［1－3］。然而，现有成果无论是经验公式、数值计算，还是无量纲理论模型均是基于宏观力学理论，假设混凝土材料为连续均匀介质而建立的，并认为弹丸在侵彻过程中保持直线运动［4－7］。但已有试验均表明［8－10］:在侵彻过程中弹丸承受骨料及砂浆的非对称力影响，存在着弯曲破坏，弹道发生较大偏转，不再是一条直线，而是偏离速度方向(图1)，这样会极大影响弹丸精确打击目标的效果。发生上述现象是由于混凝土材料具有非均质的特殊性，在细观层次上是由砂浆、粗骨料和界面过渡区(ITZ)组成的非均质多相复合材料，且各部分力学性能相差颇大，在弹丸侵彻靶体过程中存在不均匀应力场，从而导致弹丸在混凝土靶板中的运动轨迹发生变化并产生弯曲破坏。因此从细观层面上对弹丸在混凝土靶板中的侵彻过程进行研究显得十分必要。

图1 试验中弹丸弯曲破坏及弹道偏转现象

目前应用较为广泛的细观力学模型主要有以下几种:格构模型、随机粒子模型、MH细观模型、随机力学模型、随机骨料模型［11－14］。其中，随机骨料模型是由清华大学的刘光廷、王宗敏提出的。该模型将混凝土视作由骨料、水泥砂浆以及两者之间的粘结带组成的三相非均质复合材料，借助蒙特卡罗方法在试件内生成随机分布的骨料模型，骨料形状主要用圆形、椭圆、凸多边形模拟。该模型能较好地反映混凝土细观组成之间的关系，已被广泛地应用于混凝土材料的数值模型中［15－16］。本文在三维随机骨料模型投放算法的基础上，利用程序语言实现了3种不同的混凝土细观随机骨料模型，介绍了其建模方法及特点，并结合SJ.Hanchak的部分混凝土靶板侵彻试验，考察了不同模型中细观组成对弹丸剩余弹速及弹丸偏转角的影响，为细观力学层次上混凝土靶板侵彻问题数值模拟方面的研究提供一定参考。

1 细观数值模型建立

三维随机骨料模型主要根据Fuller［17］提出的理想最大密实度三维级配曲线确定试件中的骨料数量，其表达式为

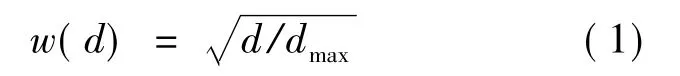
式中:w(d)为骨料通过直径为d的筛孔的质量百分比，dmax为最大骨料粒径。

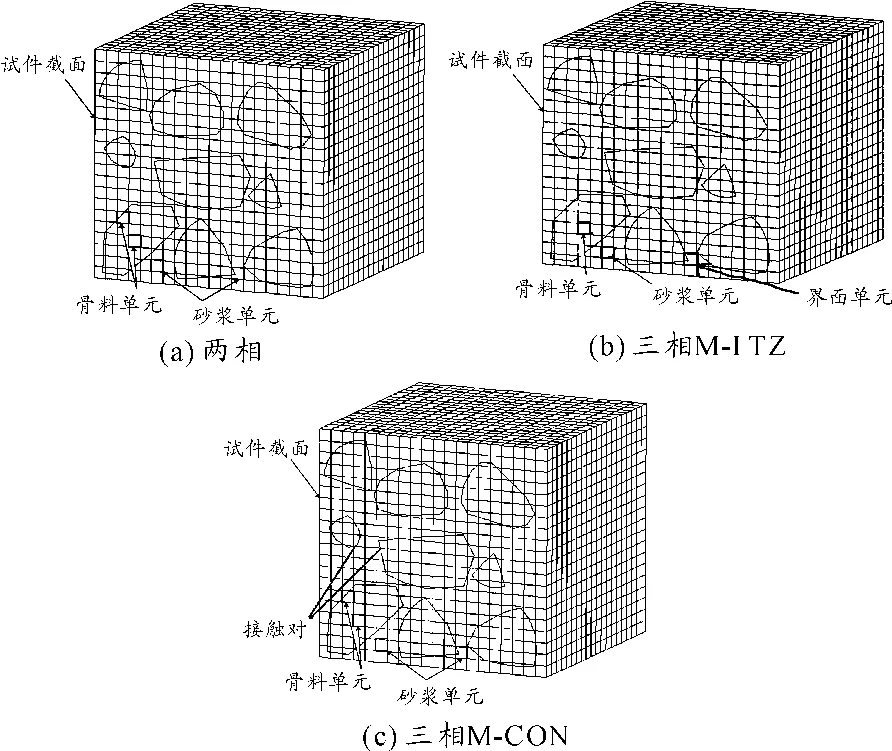
图2 3种随机骨料模型实现方式

首先根据所需模型的尺寸、骨料级配、含量等参数通过式(1)计算出其中各个粒径的数量，然后通过蒙特卡罗方法［18］对混凝土中骨料颗粒的随机分布进行模拟，接下来对颗粒的网格进行划分。三维随机骨料模型是基于背景网格的网格划分，首先将试件在给定范围内自动划分成排列整齐的正方体基本单元，单元的基本尺寸要求尽量小，形成背景网格，然后将随机分布的骨料颗粒投影到背景网格上，根据基本单元所处的位置自动完成单元类型识别和相应材料的属性赋值。

根据上述方法，采用3种不同的建模方式:1)仅考虑骨料与砂浆两相材料，基本单元面积的75%以上落入同一个骨料范围内，则该单元的类型为骨料单元，赋予骨料的材料属性，其他情况则为砂浆单元，赋予砂浆的材料属性，二者之间采用共节点方式处理(图2(a))，命名为M-WJ;2)考虑骨料、砂浆及界面三相材料，如果某个基本单元的8个节点均落入骨料的投影范围内，则该单元的类型为骨料单元，赋予骨料的材料参数;若单元的8个节点均落入砂浆的区域内，则该单元的类型为砂浆单元，赋予砂浆的材料参数;若单元的8个节点既有落入骨料范围内的又有落入砂浆范围内的，则该单元为界面单元，被赋值为界面的材料属性，三者之间同样采用共节点方式处理(图2(b))，命名为M-ITZ;3)考虑骨料、砂浆及界面三相材料，此时的网格划分仍采用方法1的思路，区别是二者之间采用接触对的方式实现界面单元的建立(图2(c))，命名为M-CON。最终得到的混凝土随机骨料模型各组成部分见图3。

图3 混凝土随机骨料模型各组成部分

2 Hanchak侵彻试验

Hanchak等［3］对混凝土单轴抗压强度为48 MPa和140 MPa的钢筋混凝土靶板分别进行了侵彻试验，得到了弹体以不同速度撞击靶板后的剩余速度和靶板的最终破坏形式。本文选取单轴抗压强度为48 MPa的钢筋混凝土靶板的侵彻试验为研究对象，进行连续介质模型及上述3种随机骨料模型在速度为360～1 000 m/s范围内的侵彻过程分析。

3 有限元模型尺寸及相关参数

根据文献［3］，在有限元计算中，为了观察模型中骨料的不均匀分布对弹体侵彻的影响和减少计算量，利用对称性建立1/2模型，其基本尺寸为610 mm×200 mm×178 mm，有限元模型见图5。由于骨料在模型中是随机分布的，为考虑不同位置骨料对侵彻的影响，采用统计学思想，选择多个弹丸位置对同一随机骨料模型的侵彻计算方法，然后通过数理统计方法得到结果变量的数值。模型简图及有限元模型见图4～5(其中方法1与3的模型在外观上一样)。试验后回收的弹丸损伤很小，且侵彻速度在1 000 m/s以下，满足刚性弹假设要求，因此模型中弹的材料模型均采用LS-DYNA中的MAT_RIGID模型，模型参数见表1。混凝土靶板采用K＆C模型［19］。该模型是混凝土损伤模型的升级版本，可以考虑应变率效应、损伤效应、应变强化和软化作用，能较好地反映混凝土在侵彻过程中的损伤效应。根据参考文献［20］及Hanchak试验计算反演得到的混凝土各相材料部分本构模型参数如表2所示。其中，接触模型采用固连断开接触类型(TSTS)。拉伸失效强度(NFLS)和剪切失效强度(SFLS)的取值参考文献［20］，并结合试验数据计算得到 NFLS(MPa)=0.58，SFLS(MPa)=0.725。采用滑移线侵蚀判断准则作为单元的失效准则，通过试算取失效应变值为0.12。

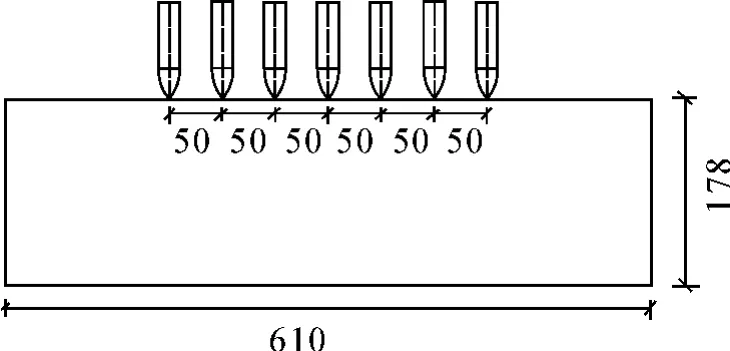
图4 模型简图

图5 有限元模型

表1 弹体材料参数

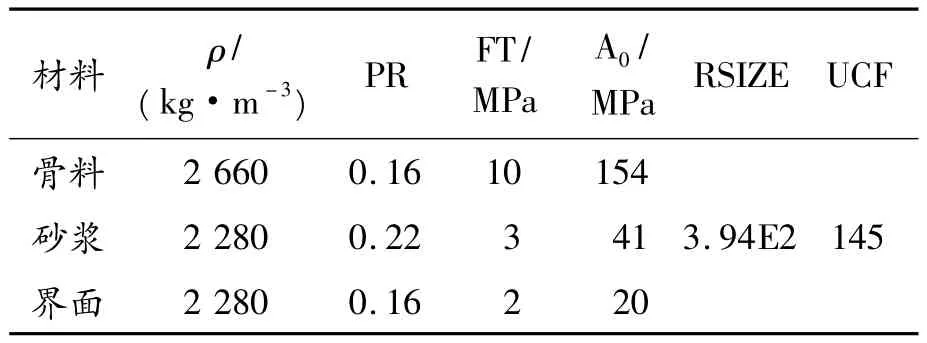
表2 模型中混凝土各相材料本构参数

4 计算结果分析

4.1 剩余速度

表3为采用4种模型对Hanchak试验中48 MPa混凝土侵彻后弹丸剩余速度值的统计。从表3可以看出:弹丸撞击速度在360～1 058 m/s的范围内，除360 m/s低速侵彻时(对于该速度及更低速度需要进一步分析)，基于连续介质和3种随机骨料模型的数值模拟结果与试验结果基本一致，误差都在20%以内，即在可以接受的范围内，说明数值计算方法可以较好地反映弹丸对混凝土靶板的侵彻过程。图6为4种模型剩余速度差值随速度变化的趋势图，可以看出:随着速度的增加，3种随机骨料模型与连续介质模型的剩余速度差值有逐渐减小的趋势。在1 000 m/s时，约为1%左右，基本可以认为数值相等。故可以得出:Hanchak试验中，在不考虑其他因素影响的情况下，当弹丸速度超过一定值时(约为1 000 m/s作用)，混凝土的细观组成对于侵彻中剩余速度的影响基本可以忽略，此时可以将其看作连续介质模型进行分析。

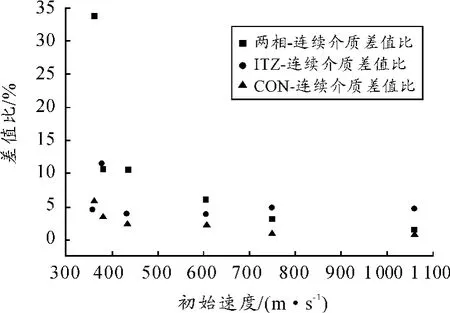
图6 剩余速度差值比随初始速度变化趋势

4.2 弹丸偏转角度

为了描述弹丸出靶时姿态的改变，在弹壳体段的中轴线上选择弹尾中点O和弹丸头部点B的连线OB与竖直方向OA所成的夹角θ来描述弹体姿态的改变。如图7所示，偏转角为正表示弹体往左侧偏转，负值为向相反方向偏转。由于试验中侵彻工况较多，为把主要篇幅留在对侵彻物理现象的分析中，故以下部分仅以典型侵彻速度为749 m/s为研究对象，着重分析不同建模方式对偏转角度的影响。

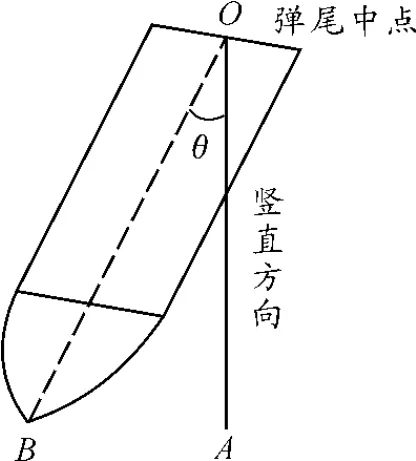
图7 弹丸偏转角计算简图

由图8可以看出:连续介质模型中，弹丸在侵彻过程中基本没有发生偏转;不考虑界面时弹丸偏转的走向与考虑界面时不同，考虑界面时弹丸更容易发生偏转。这是因为界面是混凝土材料中最薄弱的环节，弹丸在侵彻的过程中会沿着薄弱环节前进。由于M-ITZ模型有界面单元，且其参数比砂浆单元小很多，而M-CON模型没有界面单元，砂浆所占的体积含量要比M-ITZ略高，混凝土靶板的均匀性也比M-ITZ略高，因此弹丸姿态发生的偏转也比M-ITZ模型略小。

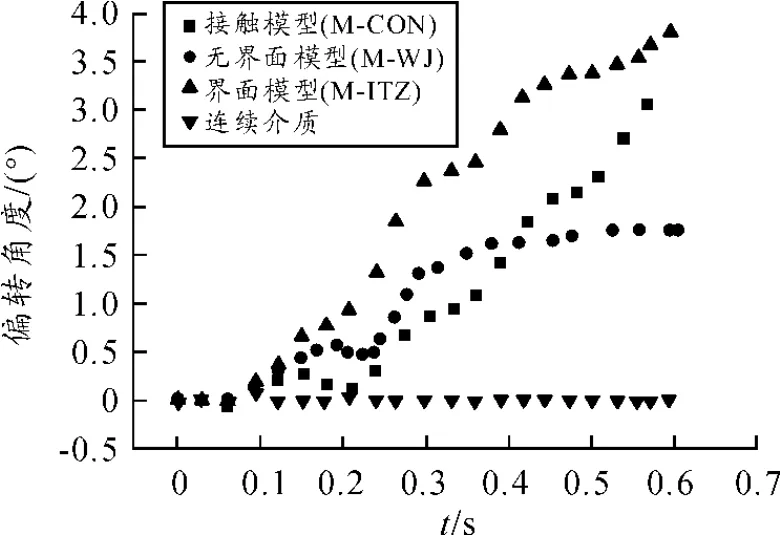
图8 749 m/s时偏转角度随侵彻时间的变化趋势

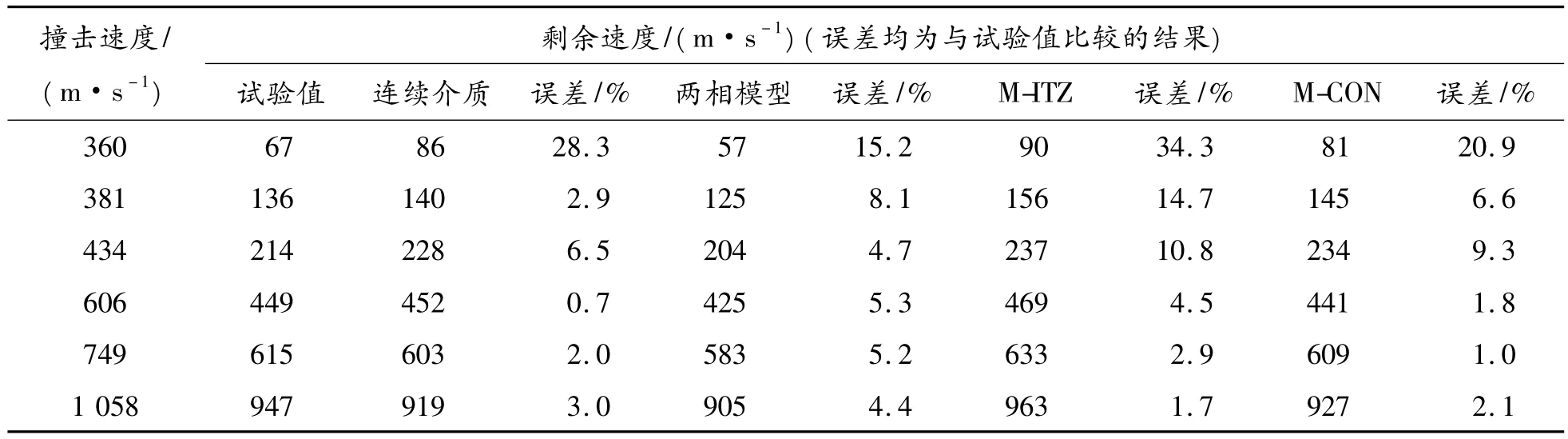
表3 4种模型模拟Hanchak试验中48 MPa混凝土的剩余速度值

5 结论

本文在随机骨料投放算法基础上，采用程序语言实现了3种不同类型的随机骨料模型，并结合Hanchak部分混凝土侵彻试验进行了数值模型对比分析，得到以下结论:

1)连续介质模型与随机骨料模型均能较好地模拟侵彻剩余速度值，且随着速度的增加，细观组成对剩余速度的影响减小。

2)随机骨料模型能反映侵彻过程中的弹丸偏转现象，3种模型的弹丸宏观偏转规律大致相同，但计算出的偏转角度差异较大，需作进一步对比分析。

［1］Penetration equations［R］.SAND97 －2426.

［2］Kennedy R P.A review of Procedures for the analysis and design of concrete structures to resist missile impact effects［J］.Nucl Eng Des，1976，7:183 －203.

［3］HANCHAK S J，FORRESTAL M J.Perforation of concrete slabs with 48 MPa(7ksi)and 140 MPa(20ksi)unconfined compressive strengths［J］.Int J Impact Enqnq，1992，12(1):1 －7.

［4］Chen X W，Li Q M.Deep penetration of a non－deformable projectile with different geometrical characteristics［J］.International Journal of Impact Engineering ，2002，27:619－637.

［5］陈小伟.穿甲/侵彻问题的若干工程研究进展［J］.力学进展，2009，39(3):316 －351.

［6］陈小伟，杨世全，何丽灵.动能侵彻弹体的质量侵蚀模型分析［J］.力学学报，2009，39(5):739 －747.

［7］He L L，Chen X W.Analyses of the penetration process considering mass loss［J］.European Journal of Mechanics A/Solids，2011，30:145 －157.

［8］何翔，徐翔云.弹体高速侵彻混凝土的效应实验［J］.爆炸与冲击，2010，30(1):1 －6.

［9］黄民荣.刚性弹体对混凝土靶的侵彻与贯穿机理研究［D］.南京:南京理工大学，2011.

［10］赵晓宁.高速弹体对混凝土侵彻效应研究［D］.南京:南京理工大学，2011.

［11］Lilliu G，Van Mier.3D lattice type fracture model for concrete［J］.Engin eering Fracture Mechanics，2003，70:927－941.

［12］Zdenfik P Bazant，Mazen R Tabbara，Mohammad T.Kazemi，et al.Random particle model for fracture of aggregate or fiber composites［J］.J Eng Mech，ASCE，1990，116:1686－1750.

［13］唐春安，朱万成.混凝土损伤与断裂－数值试验［M］.北京:科学出版社，2003.

［14］刘光廷，高政国.三维凸型混凝土骨料随机投放算法［J］.清华大学学报，2003，43(8):1120 －1123.

［15］周尚志.混凝土动静力破坏过程的数值模拟及细观力学分析［D］.西安:西安理工大学，2007.

［16］杜修力，田瑞俊，彭一江，等.冲击荷载作用下混凝土抗压强度的细观力学数值模拟［J］.北京工业大学学报，2009，35(2):214 －217.

［17］Wittmann F H.Simulation and analysis of composite structure.Mat Sci and Engrg［Z］.1985，6(8):239 －248.

［18］杨耀臣.蒙特卡罗方法与人口仿真学［M］.合肥:中国科学技术大学出版社，1999.

［19］Malvar L J，Crawford J E，Wesevich J W，et al.A New Concrete Material Model for DYNA3D［Z］.TM －94－14.3，Report to the Defense Nuclear Agency，Karagozian and Case，Glendale，CA.

［20］于庆磊，杨天鸿，唐春安，等.界面强度对混凝土拉伸断裂影响的数值模拟［J］.建筑材料学报，2009，12(6):643－649.