铁路集装箱中心站堆场混堆优化模型

王 力,朱晓宁,闫 伟,谢征宇,李秋波

(北京交通大学交通运输学院,北京100044)

铁路集装箱中心站堆场混堆优化模型

王 力,朱晓宁*,闫 伟,谢征宇,李秋波

(北京交通大学交通运输学院,北京100044)

铁路集装箱中心站堆场作为集装箱列车装卸作业与集卡提交箱作业的缓冲区,堆存策略直接影响整个中心站的作业能力和效率,本文对铁路集装箱中心站堆场混堆优化问题进行了研究.根据中心站堆场混堆作业问题的描述,建立了两阶段优化模型,第一阶段平衡中心站堆场各箱区进口箱和出口箱的箱量,第二阶段为分配到箱区的集装箱指派较优箱位,使堆存所产生的压箱数最小,并设计了启发式算法对模型进行求解.最后利用某集装箱中心站的实际数据对模型和算法进行了验证,验证结果表明,该优化模型比中心站现有的堆存策略有较大改进.

铁路运输;混堆优化;启发式算法;集装箱中心站;堆场

1 引 言

铁路集装箱中心站堆场是集装箱列车装卸作业与集卡提交箱作业间的缓冲区,是进出口集装箱临时存储的空间,是中心站的作业能力和效率的瓶颈.堆存效率直接影响整个中心站的运营状态,高效的堆存策略是中心站集装箱快速周转、铁路集装箱运输服务质量的重要保证.铁路集装箱中心站堆场堆存方法优化是铁路集装箱运输组织研究的重要方向.

中心站集装箱的堆存方式主要有两种:一种是进出口箱分别堆存方式,另一种是进出口箱混合堆存方式.目前,大部分铁路集装箱中心站采用的是进口箱和出口箱分开堆放,该方式作业复杂程度低,有利于减少不同作业间的相互干扰.但是随着中心站集装箱作业量的增大,加之集装箱堆场面积有限,为了提高堆场作业效率、节省空间资源只能使用高效的堆存方式,混合堆存方式将是今后中心站集装箱堆存的必然趋势.

铁路集装箱中心站堆场混合堆存过程包括选择堆场内箱区和选择箱区内箱位两步骤,中心站混堆优化问题属于堆场空间资源配置问题.堆场空间资源配置问题(Storage Space Allocation Problem, SSAP)主要是指根据堆场分类标准和堆放规则合理确定进出口集装箱的箱区堆存数量并指派箱位,平衡各箱区的作业量,最小化计划周期内的倒箱和翻箱次数[1].ZHANG等[2]针对港口集装箱堆场空间配置问题提出一种混堆策略,采用整数规划的方法把对每一艘船要装卸的集装箱分配到各箱区,大大减少了船舶的滞港时间;Kim等[3]应用动态规划和层次规划方法对出口集装箱的堆场分配问题进行了研究,目的是使堆场的总操作量最少;Safaei等[1]针对进口箱的箱位分配问题,以各箱区间的作业量不平衡最小化为目标,建立了整数规划模型,并采用遗传算法进行了求解;王斌[4]在文献[2]的基础上,在平衡各箱区工作量阶段引入机会约束,建立了一个实际有效的混堆模型;李建忠[5]等从平衡箱区贝位箱量和最小化集卡行驶距离入手,在滚动计划的基础上,建立了集装箱堆场空间资源动态配置模型.郑红星等[6]依据堆场混堆的作业规则定义了作业箱优先等级,以新增集装箱压箱数最小为目标对此问题构建了箱位指派优化模型;靳志宏等[7]基于集装箱装船过程中堆场翻箱作业的多阶段性特征,将翻箱作业调度优化问题归结为一个动态最短路径问题,据此构建了优化模型.

上述堆场空间资源配置问题的研究都是以港口集装箱码头为研究对象的,针对铁路集装箱堆场的研究尚不多见.江南等[8]针对铁路堆场集装箱码垛合理性及作业计划的优化进行了研究,建立了循环箱码垛模型,设计了循环箱单箱码箱取箱算法;段刚等[9]针对铁路集装箱堆场混堆区中的零散箱箱位分配问题,在集装箱到达时间和离开时间已知的条件下,建立一个计划期内以倒箱次数最少为目标的多时段动态集装箱堆场箱位分配模型.

综上所述,目前堆场空间资源配置问题的研究主要集中在港口集装箱码头,由于集装箱码头和铁路集装箱中心站在堆场布局、作业设备、堆存流程等方面都存在很大的差异,研究成果很难直接应用于中心站的堆存作业.本文以铁路集装箱中心站为研究对象,在混堆模式下建立中心站堆存优化模型,平衡各箱区的作业量,减少计划周期内堆场产生的压箱数.

2 问题描述

铁路集装箱中心站堆场由主堆场和辅助堆场组成,主堆场负责进出口重箱的堆存,辅助堆场负责空箱、专用箱、冷藏箱、维修箱、清洗箱的堆存.由于中心站集装箱堆存作业主要集中在主堆场,所以本文的堆存优化范围限定在中心站主堆场(以下简称为堆场).中心站主堆场设施设备的布局如图1所示.

铁路集装箱中心站堆场中的集装箱按照不同的状态可以分为4种类型.四类箱型的堆存作业如图2所示.

(1)IPCW型,尚在列车上的进口箱,等待卸车,堆存到堆场.此类型集装箱又可分为两类: IPCW1是由专列送至中心站的IPCW型箱,IPCW2是由小运转列车送来的零散的IPCW型箱.

(2)IPCP型,已经在堆场等待提走的进口箱.

(3)OPCW型,尚未分配到堆场的出口箱,等待被运进堆场堆存.

(4)OPCP型,已经在堆场等待装上列车的出口箱.

图1 中心站主堆场设施设备布局Fig.1 Facilities layout of center terminal main container yard

图2 四种类型箱的堆存作业Fig.2 Container storage of four types

根据堆场空间资源配置问题的优化目标,本文采用两阶段优化法,把铁路集装箱中心站堆场混堆优化问题分为2个阶段.

第1阶段 平衡各箱区的箱量,将IPCW2型、OPCW型集装箱分配到各个箱区(由于IPCW1型箱的作业特点,必然是平均分配到各箱区,所以此处只考虑IPCW2型箱),使各箱区箱量达到均衡,保证各箱区轨道门吊和箱位的均衡使用及列车、集卡迅速的装卸离站.

第2阶段 为第1阶段分配到各箱区的IPCW2型、OPCW型箱和同时期到达的IPCW1型箱指派箱位,最小化计划周期内IPCW型、OPCW型集装箱堆存产生的压箱数,从而减少提箱和装车作业时的倒箱次数,提高堆场装卸作业效率.

3 模型建立

铁路集装箱中心站一年365天连续不断运作,因此,需要选择一个固定的计划周期,采用滚动计划的方法来解决问题.根据铁路集装箱中心站堆场混堆优化问题的2个阶段,分别建立堆场箱量均衡模型M1和箱位指派模型M2.模型的建立遵照以下假设: (1)模型中所涉及的集装箱为同尺寸集装箱; (2)堆存作业时,所有箱都落在箱区,不存在直装,直卸的情况;

(3)同期到达的集装箱装卸顺序已知; (4)集装箱到达时间和离开时间已知; (5)集卡的送箱与取箱时间在计划期内不存在延误.

3.1 堆场箱量均衡模型M1

(1)符号与变量说明.

B为堆场内的箱区个数;T为一个计划周期内所拥有的计划阶段数;Ci为箱区i的堆存能力(容量)(1≤i≤B);Vi0为计划期开始时箱区i中的箱量(1≤i≤B);Vit为t时期开始时箱区i中的总箱量(1≤i≤B,1≤t≤T);VItPCW1为t时期到达的IPCW1型箱的总箱量;IP0it为t计划期开始时已分配在箱区i中,在t时期被提走的IPCP型箱的箱量(1≤i≤B,1≤t≤T);OP0it为t计划期开始时已分配在箱区i中,在t时期被装上列车的OPCP型箱的箱量(1≤i≤B,1≤t≤T);OWtk为t时期运至中心站堆场,在t+k时期装上列车的OPCW型箱的箱量(1≤t≤T,0≤k≤T-t);IWtk为t时期从列车上卸下,在t+k时期被提走的IPCW2型箱的箱量(1≤t≤T,0≤k≤T-t);OWit为t时期运至中心站分配到箱区 i中的 OPCW 型箱的箱量(1≤i≤B,1≤t≤T);OWitk为t时期运至中心站分配到箱区i中,在t+k时期装上列车的OPCW型箱的箱量(1≤i≤B,1≤t≤T,0≤k≤T-t); IWit为t时期从列车上卸至箱区i中的IPCW2型箱的箱量(1≤i≤B,1≤t≤T);IWitk为t时期从列车上卸至箱区i中,在t+k时期被提走的IPCW2型箱的箱量(1≤i≤B,1≤t≤T,0≤k≤T-t); OPit为堆存在箱区 i中在 t时期被装上列车的OPCP型箱的箱量(1≤i≤B,1≤t≤T);IPit为堆存在箱区i中在t时期被提走的IPCP型箱的箱量(1≤i≤B,1≤t≤T).

(2)目标函数.

M1模型的目标函数为

目标函数M1要把IPCW2、OPCW型箱分配到堆场各箱区,使各箱区箱量达到均衡,wi为权重系数,权重系数需根据堆场进出口箱的比重、列车装卸线和集卡作业通道的使用率、堆场箱区内空间资 源的利用率等实际情况来确定.

(3)约束条件.

式(2)～式(5)为OPCW型和IPCW2型箱的箱流约束,式(6)和式(7)为OPCP型和IPCP型箱的箱流约束,式(8)和式(9)为堆场各箱区的堆存容量约束,式(10)为t时期运至中心站堆场,在t+k时期装上列车的OPCW型箱在各箱区的分配约束,式(11)保证模型中的所有变量均为整数.

3.2 箱位指派模型M2

(1)符号与变量说明.

D同一时段分配到堆场的集装箱个数;N为箱区内的贝位个数;b为箱位的贝位编号(1≤b≤N);L为箱区内的排数;j为箱位的排数编号(1≤j≤L);F为该箱区的最大堆垛层数;f为箱位的层数编号(1≤f≤F,由下至上依次增大);M为一个无穷小的数;根据模型需要,按照排贝层的顺序描述箱位,s(j,b,f)为箱区内j排b贝位的第f层的箱位; opjbf为箱区内j排b贝位的第f层集装箱离开箱区时间(提箱或装车的时间);Sjbf为箱位s(j,b,f)处是否有集装箱,即Svjbf为第v个 堆 存 箱 是 否 指 派 到 s(j,b,f),即KOjbPf,CjbW(f-e)为OPCW型集装箱堆存在箱位s(j,b,f)对下层箱位s(j,b,f-e)的集装箱是否产生压箱,即KOjbPf,CjbW(f-e)= KIjbPfC,Wjb(f-e)为IPCW 型集装箱堆存在箱位s(j,b,f)对下层箱位s(j,b,f-e)的集装箱是否产生压箱,即KIvW为第 v个堆存箱为 IPCW 型箱时堆存产生的最小压箱数;KOvW为第v个堆存箱为OPCW 型箱时堆存产生的最小压箱数;

(2)目标函数.

M2模型的目标函数为

目标函数M2要为分配到箱区的IPCW型、OPCW型集装箱指派箱位,使堆存所产生的压箱数最小.

(3)约束条件.

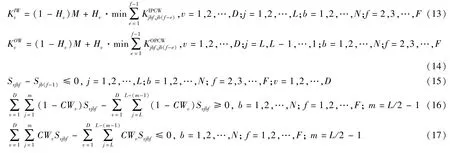
式(13)为第v个堆存箱为IPCW型箱时堆存产生的最小压箱数约束;式(14)为第v个堆存箱为OPCW型箱时堆存产生的最小压箱数约束;式(15)为第二层以上的OPCW型和IPCW型箱下方堆放集装箱,不允许悬空放置;式(16)为OPCW型集装箱的堆存偏好,尽量靠近列车装卸线,以减少装车时间;式(17)为IPCW型集装箱的堆存偏好,尽量靠近集卡作业线,以减少集卡等待时间.

4 模型求解

模型 M1的目标函数是使中心站堆场的IPCW2、OPCW型箱在各箱区的分配量和箱区总箱量达到均衡.在 M1的目标函数中,令U1=1m≤ia≤xB(OWit+IPit),U2=1m≤ii≤nB(OWit+IPit), X1=1m≤ia≤xB(IWit+OPit),X2=1m≤ii≤nB(IWit+OPit), Y1=1m≤ia≤xB(IWit+OPit+OWit+IPit),Y2=1m≤ii≤nB(IWit+OPit+OWit+IPit).将模型M1转化为

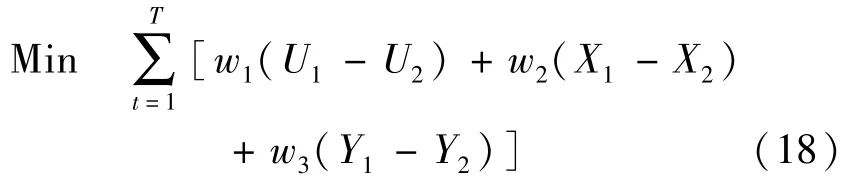
式(2)～式(11)外,增加以下约束条件

转化后的模型为整数线性规划问题,运用Lingo软件对模型M1进行求解.

根据模型M1分配到各箱区的IPCW2、OPCW型箱箱量和同时期到达的IPCW1型箱箱量,模型M2为计划周期内不同时段分配到箱区的IPCW型、OPCW型集装箱指派箱位,使堆存所产生的压箱数最小.采用启发式算法求解,其中,v为集装箱编号;n为可行解编号;K为压箱数集合;S为箱位指派集合;Svjbf为第v个集装箱指派的箱位;KInW为IPCW型箱第n个可行解增加的压箱数;KOnW为OPCW型箱第n个可行解增加的压箱数.

算法步骤如下.

Step 1 根据同时段需要堆存集装箱的计划离场时间,将各集装箱按照离场时间从晚到早进行排序,先为离场时间晚的集装箱指派箱位,保证这个时段堆存的集装箱之间不构成压箱.参数初始化,令v=1,K={Ø},S={Ø},j=1,b=1.转入Step 2.

Step 2 判断第v个箱的箱型,如果为OPCW型箱转入Step 3,否则转入Step 6.

Step 3 判断箱区1至m(m=L/2-1)排内是否有空贝位,有空箱位则令 S=S∪ {Svjbf}、v=v+1,如果 v≤ D,转入 Step 2,否则转入Step 9;如没空箱位,转入Step 4.

Step 4 将该箱指派到j排b贝位的第f层,判断是否为可行解,如为不可行解,转入Step 5;如为可行解,则将该可行解KOnW与KOn-W1进行比较.如果KOnW≥KOn-W1,令KOnW=KOn-W1,转入Step 5;如果KOnW＜KOn-W1,令KOvW=KOnW,转入Step 5.

Step 5 令b=b+1,如果b≤N,转入Step 4继续计算;否则令j=j+1,如果j≤L,转入Step 4继续计算;如果j＞L,令K=K∪{KIvW}、S=S∪{Svjbf},第v个箱指派完毕.令j=1,b=1,v=v+1,如果v≤D,转入Step 2;否则转入Step 9.

Step 6 判断箱区L至L-(m-1)(m=L/2-1)排内是否有空贝位,有空箱位则令S=S∪{Svjbf}、v=v+1,如果v≤D,转入Step 2,否则转入Step 9;如没空箱位,转入Step 7.

Step 7 令j=L,将该箱指派到j排b贝位的第f层,判断是否为可行解,如为不可行解,转入Step 8;如为可行解,则将该可行解KInW与KInW-1进行比较.如果KInW≥KInW-1,令KInW=KInW-1,转入Step 8;如果KInW＜KInW-1,令KIvW=KInW直接转入Step 8.

Step 8 令b=b+1,如果b≤N,转入Step 7继续计算.否则令j=j-1,如果j≥1,转入Step 6继续计算;如果j＜1,令K=K∪{KOvW}、S=S∪{Svjbf},第v个箱指派完毕.令j=1,b=1,v=v+1,如果v≤D,转入Step 2;否则转入Step 9.

Step 9 根据压箱数集合K,计算最小压箱数,并输出S,算法结束.

5 算例分析

本文以某铁路集装箱中心站为例,该中心站主箱区共分为4个箱区,每个箱区共30贝位,每个贝位为6排,最大堆垛层数为2层,每个箱区共360个箱位;选择1 d作为一个计划周期,6 h一个时段,每天分为4个计划阶段;计划期内OPCW,IPCW1、IPCW2、IPCP、OPCP型箱的箱量如表1所示,IPCP、OPCP型箱的装车和提箱计划如表2所示.

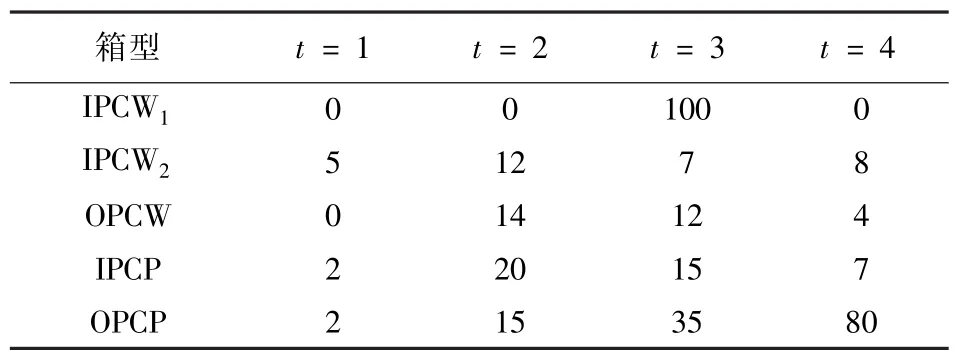
表1 计划期内四种箱型的箱量(TEU)Table 1 Four types of container volumes in planning period(TEU)

根据两阶段优化模型M1和M2,分别运用Lingo和Matlab求解上述算例,得到OPCW,IPCW1、IPCW2型箱在各箱区的分配结果如表3所示,计划期内堆场各箱区产生的压箱数如表4所示.

表2 IPCP、OPCP型箱的装车和提箱计划(TEU)Table 2 Loading planning of IPCP and OPCP(TEU)

表3 OPCW、IPCW1、IPCW2型箱在各箱区的分配结果(TEU)Table 3 Distribution of OPCW、IPCW1and IPCW2(TEU)

表4 计划期内堆场各箱区产生的压箱数 Table 4 Overlapping amount of container yardin planning period(TEU)

模型M1的目标函数为5TEU,根据经验,箱区间箱量的最大量和最小量的差都在10以上,模型M1有效地平衡了各箱区的箱量.模型M2的目标函数为15个,与中心站目前使用的随机分配方法所产生的压箱数28个相比,模型M2有效地减少了箱位指派时产生的压箱数.因此,采用本文提出的两阶段优化模型,可以有效地均衡中心站堆场各箱区的箱量,减少箱位指派时产生的压箱数,提高中心站堆场的堆存效率.

6 研究结论

本文针对铁路集装箱中心站主箱区集装箱混合堆存作业问题,建立了两阶段优化模型,第一阶段平衡堆场各箱区进口箱和出口箱的箱量,第二阶段以堆存所产生的压箱数最小为目标为分配到箱区的集装箱指派较优箱位,并设计了启发式算法对模型进行求解,最后利用算例对模型与算法进行了验证.算例结果表明,模型与算法能够均衡堆场各箱区箱量并有效减少堆存所产生的压箱数.针对计划期内集卡取箱和送箱时间的不确定性改进模型是下一步的研究方向.

[1]Bazzazi K,Safaei N,Javadian N.A genetic algorithm to solve the storage space allocation problem in a container terminal[J].Computers& Industrial Engineering, 2009,56(1):44-52.

[2]Zhang C Q,Liu J Y,Wan Y W.Storage space allocation in container terminals[J].Transportation Research Part B,2003,37(10):883-903.

[3]Kim K H,Park Y M,Ryu K R.Deriving decision rules to locate export containers in container yards[J]. European Journal of Operational Research,2000,124 (1):89-101.

[4]王斌.集装箱码头堆场的一种动态随机堆存方法[J].系统工程理论与实践,2007,27(4):147-153. [WANG B.Dynamic and stochastic storage model in a container yard[J].Systems Engineering-Theory& Practice,2007,27(4):147-153.]

[5]李建忠,丁以中,王斌.集装箱堆场空间动态配置模型[J].交通运输工程学报,2007,7(3):50-55.[LI J Z,DING Y Z,WANG B.Dynamic space deployment model of container storage yard[J].Journal of Traffic and Transportation,2007,7(3):50-55.]

[6]郑红星,杜亮,董键.混堆模式下集装箱堆场箱位指派优化模型[J].交通运输系统工程与信息,2012,12 (1):153-159.[DENG H X,DU L,DONG J. Optimization modelon containerslotallocation in container yard with mixed storage mode[J].Journal of Transportation SystemsEngineering and Information Technology,2012,12(1):153-159.]

[7]靳志宏,毛钧,李娜.基于混合动态规划的集装箱堆场贝位内翻箱作业调度优化[J].交通运输系统工程与信息,2011,11(6):131-136.[JIN Z H,MAO J, LI N.Scheduling of relocating containers within a bay in container yard based on hybrid dynamic programming [J].Journal of Transportation Systems Engineering and Information Technology,2011,11(6):131-136.]

[8]江南,钱迈,渠洪涛,等.集装箱堆场作业计划模型及算法[J].铁道学报,2009,31(5):8-16.[JIANG N, QIAN M,QU H T,et al.Model and algorithm of container yard operation plans[J].Journal of the China Railway Society,2009,31(5):8-16.]

[9]段刚,陈莉,陈志忠,等.铁路集装箱堆场混堆区箱位分配优化模型与算法[J].铁道学报,2011,33(7):1-7.[DUAN G,CHEN L,CHEN Z Z,et al.Model and algorithm for optimization of container storage allocation in mixed storage area of railway container yard[J]. Journal of the China Railway Society,2011,33(7): 1-7.]

Optimization Model of Mixed Storage in Railway Container Terminal Yard

WANG Li,ZHU Xiao-ning,YAN Wei,XIE Zheng-yu,LI Qiu-bo
(School of Traffic and Transportation,Beijing Jiaotong University,Beijing 100044,China)

Railway container yard is a buffer area of loading and unloading freights between train and truck.The storage efficiency thus significantly impacts the performance ability and productivity of railway container terminal.This paper examines the optimization problem of mixed storage in railway container terminal and proposes a two-stage optimization model considering the description of mixed storage operation in container yard.In the first stage,output and input container volumes are balanced among various blocks. To reduce the container overlapping amounts,the relative optimal slots are allocated in the second stage.The algorithm to solve the problem is presented based on heuristic algorithm.The field data from certain railway container terminal is used to test the proposed method and the result shows its effectiveness and efficiencies.

railway transportation;mixed storage optimization;heuristic algorithm;container terminal; container yard

U294.3

A

U294.3

A

1009-6744(2013)02-0172-07

2012-11-22

2013-01-10录用日期:2013-01-23

国家自然科学基金(60870014).

王力(1981-),男,内蒙古包头人,博士生.

*通讯作者:xnzhu@bjtu.edu.cn