ETC系统对收费站服务水平的影响研究
张晨琛,王艳辉*,贾利民
(北京交通大学a.轨道交通控制与安全国家重点实验室;b.交通运输学院,北京100044)
1 引 言
随着我国高速公路建设里程的迅猛增加和汽车保有量的快速增长,高速公路交通需求和交通流量激增,加大了高速公路收费站的通行压力,尤其是在交通高峰时段,收费站服务效率大大下降,当服务水平不能满足交通量需求时,收费广场内将会形成交通拥堵和长排队现象[1],严重影响了高速公路的服务质量,同时也带来了巨大的安全隐患.采用电子不停车收费系统(ETC,Electronic Toll Collection)可以有效解决这一问题.
近年来,采用ETC技术改善车流拥堵状况已成为国际趋势,在美国、欧洲和日本都得到了广泛应用.电子收费的通行能力是人工收费通行能力的3~8倍,ETC不仅能够提高收费站的通行能力、缓解收费站因缴费而产生的拥挤车流、节省扩建收费站的各种成本,而且还可以减轻收费人员的劳动强度、减少因缴费停车导致的环境污染、提高收费管理水平等.
目前,针对ETC系统的研究主要集中在ETC车道数布局、设置方案及其在各方面产生的影响分析.Bornoico等人研究了已知不同收费方式的车流量条件下,利用随机排队模型计算不同收费方式的车道数问题[2].刘伟铭等人根据车辆达到的随机特点,运用排队论方法建立起4x收费系统费用损失最小为目标的优化模型,然后利用遗传算法求得在不同ETC使用率情况下的最佳车道配置[3];周崇华等基于排队论理论和增量效益成本比率分析原理,建立了以增量效益成本比率最大化为目标的 ETC车道优化配置模型[4].Levinson等人研究了ETC车辆加、减速状况对收费站延误的影响[5].陆健等人在定性分析了ETC系统在交通性能、交通安全、能源与环境及收费运营等方面产生影响的基础上,对如何度量有关ETC系统在这几方面产生的效益进行了研究[6].ETC系统对于收费站服务水平的影响分析,尚缺乏相关研究.
鉴于此,本文在对北京市周边多条高速公路收费站实地调研和现有研究成果的基础上,对收费系统和收费系统内车辆个体的行为特征进行了详细分析,建立了一种基于元胞自动机模型的ETC收费站交通流模型,仿真分析了ETC系统对收费站服务水平的影响程度,为管理者合理设置ETC收费站车道数、提高收费站服务水平提供了理论依据.
2 ETC收费站交通流模型
2.1 基本问题说明
(1)本文所指的ETC收费站特指同时具有ETC车道和人工收费(MTC,MannualToll Collection)车道的收费站.
(2)考虑车辆付费方式的差异,车辆被分为两类:一类是电子付费车辆,这类车辆安装有车载装置OBU(On Board Unit);另一类是现场付费车辆,这类车辆不配备相应车载装置.电子付费车辆可以根据实际的交通流状况选择ETC或MTC收费车道,而现场付费车辆只能选择MTC收费车道.
(3)收费站主要包括高速公路基本路段、收费通道和收费广场过渡段三部分[7].
①高速公路基本路段.
依据《公路交通标志和标线设置规范》要求,在距离收费广场渐变段起点2 km、1 km、500 m处应设置收费站预告标志,司机在见到2 km预告标志牌起开始减速,准备进入收费广场.为此,本文定义收费站2 km预告标志起至收费站标志路段为高速公路基本路段.该路段车道数为k,长度为La=2 000 m,宽度为 Wa=(3.75·k)m,分别记作A1,A2,…,Ak,2≤ k≤4 ,如图1中 A 段所示.
②收费通道.
车辆接受收费服务所经过的通道.收费通道数为n,长度为Lc,宽度为Wc=(5.4·n)m,有C={C1,C2,…,Cn},C=C'∪C″,其中C'为ETC 收费通道集合,设置为限速区间,限速值为vc;C″为MTC收费通道集合,ETC收费通道数量记为nE,MTC收费通道数量记为nM,n=nE+nM,2≤n<10,如图1中C段所示.
③收费广场过渡段.
连接高速公路基本路段和收费通道的等腰梯形区域.该梯形的边与高速公路基本路段的夹角为α(3°≤α≤5°),上底长度为Wa,下底长度为Wc,长度为将该区域划分为n条路段,有 B={B1,B2,…,Bn},B=B'∪B″,其中 B'为ETC车道集合,设置为限速区域,限速值为vc,B″为MTC车道集合,如图1中B段所示.
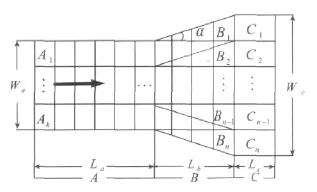
图1 ETC收费站系统示意图(单向)Fig.1 Schematic diagram of ETC plaza system(unidirectional)
2.2 模型构建
基于上述说明及对实际车流运行特性的调研分析,本文将在几种常用交通流元胞自动机模型的基础上针对以下几种情况分别使用特定的规则:车辆在A段上行驶;车辆从A段进入B段;车辆在下一个时间步会到达C段;车辆在C段接受收费服务[8].
(1)A段内车辆根据k值的变化选择不同的模型进行更新[9-11]
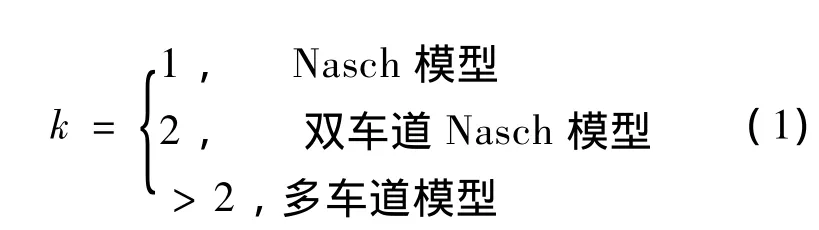
在更新过程中,考虑大型车和小型车的车辆最大限速和长度不同,令表示车辆的最大限速值集合,其中为大型车的最大限速值;为小型车的最大限速值.表示车辆长度的集合,其中为大型车车长;为小型车车长.
(2)根据实地调研情况,B段中车辆交互频率高、强度大,容易发生拥堵,甚至导致交通安全事件发生,是本文研究的重点.
①车辆进入A段的最后一个元胞.
(a)电子收费车辆演化规则.
假定其会跟随B段中离它较远的车辆,即进入集合
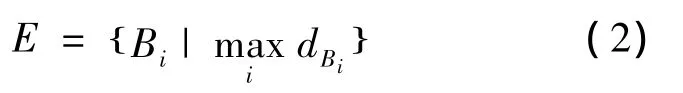
的元素Bi路段,其中dBi=xBilast-xAklead-lveh,i=1,2,…,n;xBilast为 Bi路段最后一辆车的位置;xAklead为Ak路段头车的位置.当dB1=dB2=… =dBn时,以相同概率随机选择路径.
(b)人工付费车辆演化规则.
设MTC车道集合B″中含有s个元素,则车辆会进入集合
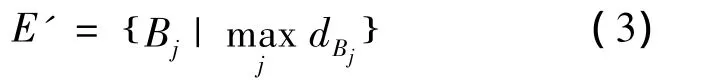
的元素 Bj路段,其中 dBj=xBjlast-xAklead-lveh,i=1,2,…,n;xBjlast为Bj路段最后一辆车的位置;xAklead为Ak路段头车的位置,Bj∈B″.
②车辆进入B段.
(a)电子收费车辆换道规则.
R3进行换道:以概率p令lanen(t)=lanen(t).为了避免发生碰撞,要从右向左依次对每个车道进行处理.
(b)人工付费车辆换道规则
R3进行换道:以概率p令lanen(t)=lanen(t).为了避免发生碰撞,要从右向左依次对每个车道进行处理.
(c)换道完成后,设置vmax=vc,再根据单车道Nasch模型进行更新.
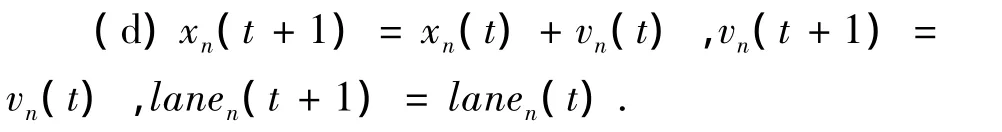
(3)xn(t)<xtoll并且xn(t+1)>xtoll.
①电子收费车辆.
设置vmax=vc,根据开口边界条件及Nasch更新规则,车辆n驶出该路段.
②人工付费车辆.
我们令xn(t+1)=xtoll,Tw=T.T是车辆在收费站停留的总时间.实地调研数据表明,根据车型的不同,大型车和小型车的停留时间不同,即T={Tb,Ts}.
(4)xn(t)=xtoll.
①电子收费车辆.
设置vmax=vc,根据开口边界条件及Nasch更新规则,车辆n驶出该路段.
②人工付费车辆.
我们需要检测Tw的值:如果Tw>0,那么Tw=Tw-1,并且xn(t+1)=xtoll;如果Tw=0,根据开口边界条件,车辆n驶出该路段.xtoll则表示收费站的位置;Tw是车辆仍然需要在收费站停留的时间.
3 收费站服务水平仿真分析
3.1 收费站服务水平
收费站服务水平是衡量收费站内部交通流运行条件,以及驾驶员和乘客所感受的服务质量的一项指标.收费站服务水平的效率指标主要包括速度、平均延误、平均排队长度和饱和度(v/c)等[12-14].目前,关于收费站服务水平的评价方法还没有一个统一的标准.考虑到ETC收费站的特殊性,研究选用收费站平均延误作为衡量收费站服务水平的指标.
收费站平均延误计算公式
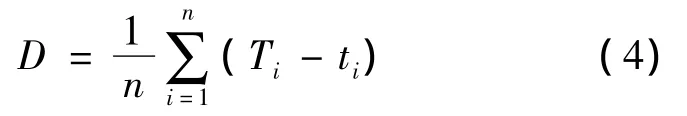
式中 D为收费站平均延误;n为仿真时间内通过收费站系统的车辆总数;Ti为第i辆车通过收费站的行程时间;ti为第i辆车的行驶时间.
3.2 仿真应用分析
以标准标定参数为基准点,模拟交通量、ETC使用率及ETC车道数量变化条件下的收费站服务水平变化情况,便于比较分析不同仿真方案的仿真结果.
(1)仿真标准参数标定.
设定模型参数中k=2,n=4,nE=0,元胞长度为7.5 m/cell,La=2 000 m(即约267 cell),αm(即约18 cell),Lc=7.5 m(即1 cell)cell)},T={Tb,Ts}={12 s,8 s},设置道路入口处的4个元胞为发车区,ETC使用率为0,采用开放式边界条件,大型车比例Pm=0.3,设置进车概率Pe=0.5,车辆随机慢化概率Ps=0.25,车辆换道概率Pc=0.25.设定模拟运行步数5 000步,时间步长为1 s.
(2)仿真方案设计.
为了便于比较分析ETC系统对收费站服务水平的影响程度,选择ETC车道数量、ETC使用率和交通流量三个参数构建仿真方案.
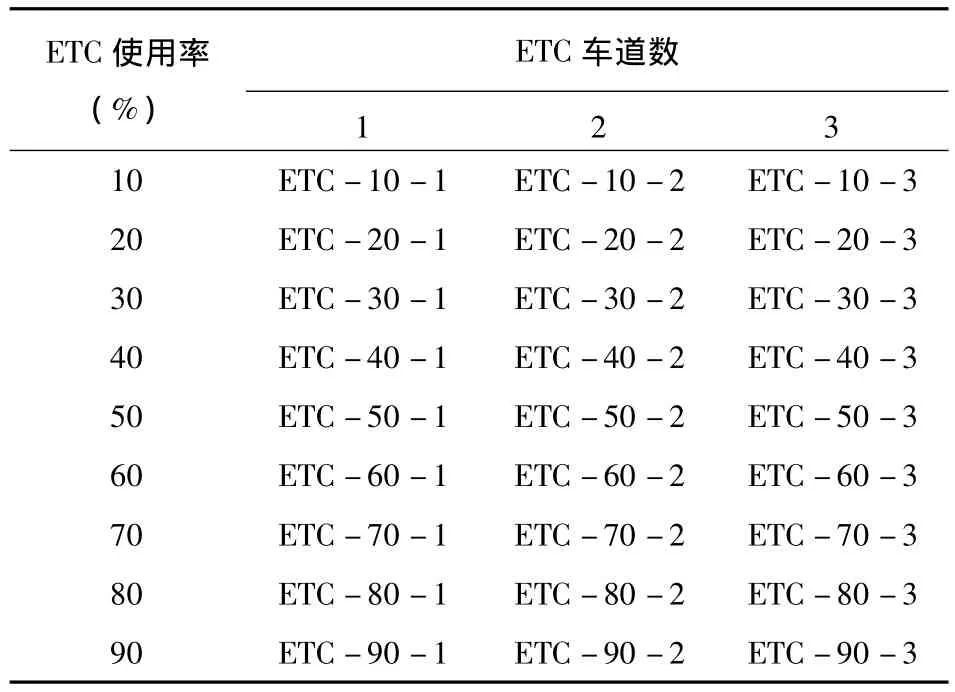
表1 仿真方案Table 1 Simulation program
针对每个仿真方案都设置不同的交通流量,交通流量范围为[800 veh/h,1 600 veh/h],通过运行仿真程序,可以得到不同仿真方案下收费站的平均延误.
(3)仿真结果分析.
选取仿真方案中ETC使用率为30%、60%和90%的收费站平均延误仿真结果进行分析.
①从仿真结果来看,当ETC使用率为30%时(如图2所示),配置1条或2条ETC车道的收费站服务水平高于不设置ETC车道的收费站服务水平.以交通量980 veh/h为临界点,当交通量低于980 veh/h时,配置1条ETC车道比配置2条ETC车道效果更佳,当交通量高于980 veh/h时,配置2条ETC车道比配置1条ETC车道效果更佳,当交通量过小时,配置3条ETC车道效果不佳.
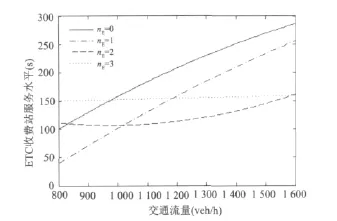
图2 ETC使用率为30%的仿真结果Fig.2 Simulation results of the ETC use ratio of 30%
② 当ETC使用率为60%时(如图3所示),配置1条、2条或3条的ETC车道的收费站整体服务水平均高于不配置ETC车道的收费站服务水平.当交通量低于1 400 veh/h时,配置1条ETC车道比配置2条和3条ETC车道效果更佳,当交通量高于1 400 veh/h时,配置2条ETC车道比配置1条和3条ETC车道效果更佳.
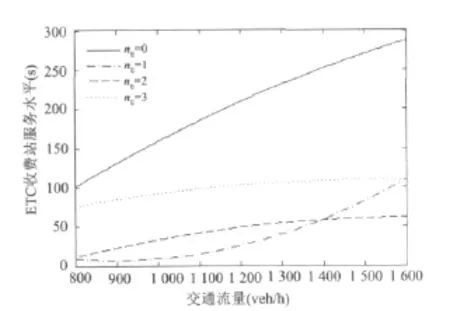
图3 ETC使用率为60%的仿真结果Fig.3 Simulation results of the ETC use ratio of 60%
③ 当ETC使用率为90%时(如图4所示),配置1条、2条或3条ETC车道的收费站整体服务水平均高于现状,且在任何交通量下,配置3条ETC车道效果均为最佳.
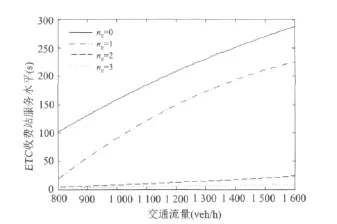
图4 ETC使用率为90%的仿真结果Fig.4 Simulation results of the ETC use ratio of 90%
4 研究结论
基于对高速公路ETC收费站实地调研结果的分析,主要得到以下研究成果:
(1)结合实地调研情况,对高速公路ETC收费站系统构件进行了形式化描述,为后续研究奠定了基础;
(2)通过分析各个系统组分中车辆的行为特征、车辆及收费通道的分类特征,建立了适合描述高速公路ETC收费站交通流运行状况的元胞自动机模型;
(3)定义了衡量ETC收费站服务水平的效率指标,运用构建的交通流模型,仿真分析了不同仿真方案下4车道封闭式收费站ETC车道数的最优配置数量,该结论同样适用于其他4车道封闭式收费站.
在后续研究中,将进一步丰富收费站服务水平的效率评价指标,并研究多车道封闭式收费站ETC车道数量配置最优解的分布规律.
[1]梁夏.上海高速公路收费站拥堵状况和扩容改造措施[J].中国市政工程,2010(4):4-5.[LIANG X.On congestion condition and expanding measures to Shanghai highway toll stations[J].China Municipal Engineering,2010(4):4-5.]
[2]Boronico J S,Siegel P H.Capacity planning for toll roadways incorporating consumer wait time costs[J].Transportation Research Part A:Policy and Practice,1998,32(4):297-310.[3]刘伟铭,李蓉,李宇.基于遗传算法的车道配置优化模型[J].广西交通科技,2003,28(107):24-27.[LIU W M,LI R,LI Y.The optimization method of tollgates deployment based on genetic algorithms [J]. Guangxi Communication Science & Technology,2003,28(107):24-27.]
[4]周崇华,周九州,苏志哲.基于排队论和增量效益成本比率最大化的ETC车道配置模型研究[J].交通运输系统工程与信息,2009,9(5):77-84.[ZHOU C H,ZHOU J Z,SU Z Z.Modeling ETC lane deployment based on queuing theory and incrementalbenefit-cost ratio maximum [J]. Journal of Transportation Systems Engineering and Information Technology,2009,9(5):77-84.]
[5]Levinson D,Chang E.A model for optimizing electronic toll collection systems[J].Transportation Research Part A:Policy and Practice,2003,37(4):293-314.
[6]陆健,丁纪平,叶凡,等.ETC系统效益评价指标体系[J].交通运输工程与信息学报,2003,1(1):75-80.[LU J,DING J P,YE F,et al.ETC System benefit evaluation and performance index system[J].Journal of Transportation Engineering and Information,2003,1(1):75-80.]
[7]交通运输部公路科学研究所.高速公路收费站及收费广场设计规范[DB/OL].http://www.docin.com/p-201537624.html,2000-6/2011-8. [Research Institute of Highway Ministry of Transport.Specification for design of expressway toll station and toll plaza[DB/OL].http://www.docin.com/p-201537624.html,2000-6/2011-8.]
[8]Jiang R,et al.The lane expansion effect of the tollbooth system on the highway[J].International Journal of Modern Physics C,2004,15(5):619-628.
[9]Nagel K,Schreckenberg M.A cellular automaton model for freeway traffic[J].Journal de Physique I France,1992(2):2221-2229.
[10]Chowdhury D,Wolf D E,Schreckenberg M.Particle hopping models for two-lane traffic with two kinds of vehicles:Effects of lane changing rules[J].Physica A,1997(235):417-439.
[11]Bonzani I,Gramani Cumin L M.Modelling and simulations of multilane traffic flow by kinetic theory methods[J]. Computer & Mathematics with Applications,2008,56(9):2418-2428.
[12]Transportation Research Board.Highway capacity manual 2000[M].WashingtonD C:National Research Council,2000.
[13]Klodzinski J,Al-Deek H.New methodology for defining levelofservice attollplazas[J]. Journalof Transportation Engineering,2002,128(2):173-181.
[14]邹智军,杨东援.微观交通仿真中的车道变换模型[J]. 中国公路学报,2002,15(2):105-108.[ZOU Z J,YANG D Y.Lane changing model for micro traffic simulation [J]. ChinaJournalofHighway and Transport,2002,15(2):105-108.]

