一种基于CBD的构件优化选择模型

杨 曦

（福州大学阳光学院，福建福州350015）

一种基于CBD的构件优化选择模型

杨 曦

（福州大学阳光学院，福建福州350015）

构件优化选择模型一直是基于构件开发领域的研究热点，但过去的二十年间这方面的理论研究一直未取得太大的成果，尤其在选择构件时几乎都未考虑构件间内聚和耦合的影响.本文提出一种构件优化选择的数学模型，为如何选择构件提供一种可量化的依据.该模型将CBD开发的功能性评级及构件的内聚性和耦合度进行了量化，试图在功能评级和内聚性最大化，而耦合度最小化的情况下，应用遗传算法寻求最佳的构件选择方案.最后，通过一个小型金融系统的案例来验证该模型的有效性.

CBD开发；耦合度；模块化；遗传算法

1 引言

大型软件系统的有效性开发一直以来都是软件工业界的挑战.许多概念和方法的提出，比如抽象数据类型、结构化编程、面向对象方法、设计模式和建模语言等，都是为了提高软件系统开发的有效性.而近年来，基于构件的开发CBD(ComponentBasedDevelopment)则成为一种最具潜力的软件有效性开发方法[1].而所谓构件则被定义为有特定合约接口且有明确上下文依赖的合成化单元[2].CBD关注于按功能或逻辑将系统分解成接口定义良好的构件集，从而可以选择合适的商业成品构件(CommercialOff-the-ShelfComponent，COTS)来集成软件系统.这种方法已证实可以大大缩短开发时间并使得开发出来的系统具有更好的可维护性.

许多研究试图为软件的模块化定义标准、开发度量，以量化模块化行为.传统基于模块的软件系统开发，通常都依循高内聚、低耦合的设计原则.内聚度高的模块具有较好的可重用性，而低耦合性则使得软件系统更易维护.文献[3]提出一种基于耦合和内聚的软件质量度量方法，该方法给出了一些好的编程实践特性，旨在减少维护及修改的成本.文献[4]探讨了软件系统模块化的标准，并将此标准在传统和非传统的方式下进行了评估.文献[5，6]提出了一种新的度量集，用于分析大型系统模块间的交互性和评估软件模块化的质量.文献[7]基于最小耦合度、最高内聚性的标准，提出一种定量的方法用于测量和评估软件模块化的方案.文献[8]提出一种构件选择的两阶段决策模型，通过案例检索和(0-1)整数目标规划，实现最优构件组合选择.文献[9]提出一种基于线性规划的构件优化选择机制，将构件选择问题转化为在一组线性约束条件下目标函数优选的数学问题，利用回溯法求得最优构件选择方案.

研究表明，在可相互替换的软件构件集中，通常认为这些构件应该具有相同的功能.而事实上，因为软件构件由不同构件厂商提供，所以功能上就可能存在差异.因此，在选择商业构件时，构件对于CBD功能需求的契合度也必须加以考虑.之前关于模块化及构件选择的研究，虽然从不同角度给出了构件选择的依据和方法，但基于最小耦合度及最大内聚性的定量方法都无法妥善解决如何为不同软件模块(Module)选择最合适的构件，更没有考虑到构件对于系统的功能性贡献因素，而这三种因子对于软件系统的可重用性、易维护性及系统可用性等质量属性又起着关键的决定作用.所以，本文以最小耦合度、最大内聚性为因子，同时将软件功能契合度最大化的因素也加以考虑，用于软件构件的选择.基于这些因子构建的构件优化选择模型是一组带约束的二进制二次方程，故引入遗传算法解决优化选择的进化问题.

2 构件选择的优化模型

2.1 基础选择模型

将内聚性和耦合度做为构件选择的考虑因子这方面，本文引用文献[7]的定量测量内聚和耦合的方法，用模块内耦合度(Intra-modular Coupling Density，ICD)的概念来表示模块的内聚和耦合间的定量关系，公式如下：

CIIN是模块内部构件与构件之间的交互数，而CIOUT是某一模块中的构件与另一模块的构件之间的交互数.如图1所示，CIIN=6(图中实线的数目)，CIOUT=6(图中虚线的数目)，则ICD=0.5.本文ICD用于表示耦合和内聚的比例关系，这样，模块j的内聚与所有交互数的比例可以表示为ICDj.

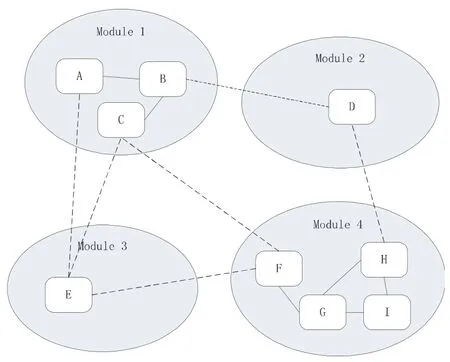
图1 CBD软件模块的内聚和耦合

然而，我们很容易发现，若有些模块只有一个构件(比如图1中的模块2与模块3)，则这些模块ICD的值势必为0.为弥补这个缺陷，我们将公式(1)的分子简单地加上1，于是得到如下表示第j个模块耦合度的公式：

众所周知，高内聚、低耦合可以使软件系统具有较高的可维护性.所以ICD的值对于以CBD方式开发的软件系统的可维护性而言至关重要.

2.2 优化选择模型

CBD开发首先应该将模块识别出来，并且每个模块至少要有一个构件组成.软件构件是包含可执行程序代码的软件产品，通常由第三方构件厂商提供.CBD开发中一个最主要的问题是如何从市场中选择合适的构件来组成模块.通常，CBD采用自顶向下的开发方法.这种方法，首先需定义功能/客户需求.然后再确定模块的数目及特性，最后选择合适的构件组成模块.选择构件的原则必须遵循模块内部的构件之间的交互最大化(最大内聚性)，而模块与其他模块的构件之间的交互最小化(最小耦合度).

为构建构件选择的优化模型，需要先定义、说明一些参数，如表1所示：

表1 构件优化选择模型参数表

则第j个模块的内聚值(CIIN)j的计算公式为：

第j个模块的交互性(包括内聚和耦合)CAj的计算公式为：

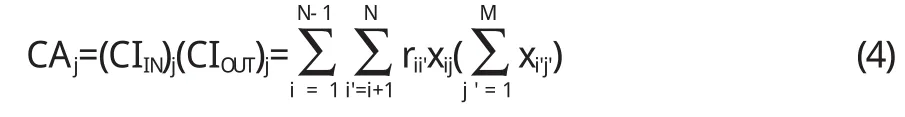
软件系统所有模块的交互性CA的计算公式为：

所有模块内聚值的和CIIN为：

这样，基于上一节确定的标准(即公式2)，我们构建的构件选择的优化数学模型如下：

显然，为了优化选择构件，目标函数(7)是软件系统功能性最大化的量化公式，目标函数(8)是ICD值最大化的量化公式，即基于系统模块间耦合度最小，而模块本身内聚度最大的情况构建的计算公式.等式(9)显示从待选构件集中只能为所服务的模块选择一个构件.不等式(10)限定每个模块里至少要有一个构件.为了简化优化模型，我们用Fmax和Fmin分别表示F的最大值和最小值，用Imax和Imin表示ICD的最大值和最小值，将多目标优化模型转化为集成的单一目标优化模型.这样，目标函数(7)～(9)转化为：

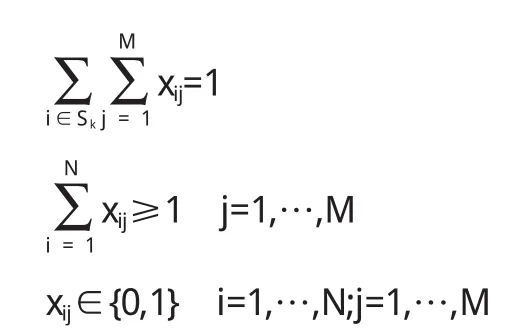
这里，wf、wl分别代表F和ICD在系统中的权重，故wf+wl=1.Fmax的值可以通过求解(7)、(9)、(10)、(11)而确定.同理，Fmin可以通过求解(14)、(9)、(10)、(11)来获得.而Imax可以通过求解(8)、(9)、(10)、(11)获得，Imin可以通过求解(15)、(9)、(10)、(11)获得.

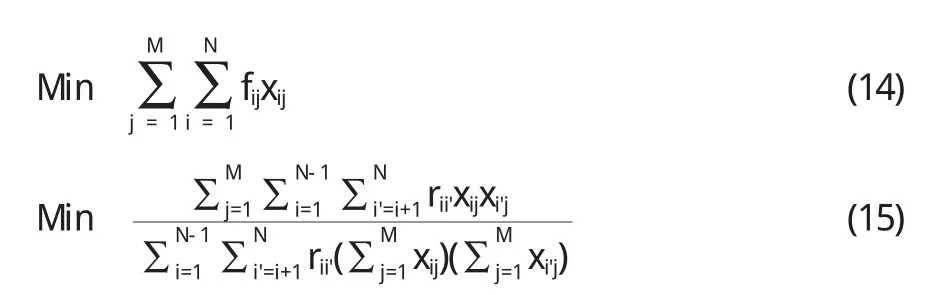
2.3 基于遗传算法的优化选择

由于优化模型是带约束的二元二次方程，所以优化选择问题事实上是一个NP完全问题，而解决这类问题最重要的就是如何有效解决“组合爆炸”的问题，显然遗传算法[10]是一种明智选择.

我们通过一个案例来分析优化选择模型的有效性，其中遗传算法染色体表示如图2(a)所示.在这个案例中，将软件系统分成三个模块m1、m2、m3，而由市面上选定的12个商业构件(sc1～sc12)组成5个可选构件集(s1～s5)，每一个可选集中只有一个构件可以被选中用于某个特定模块，同一可选集中的构件都提供相似的功能并可相互替换.如图2所示，sc2、sc4、sc8、sc10及sc12分别从s1、s2、s3、s4、s5中被选中.

图2 染色体表示及ZIP编码示例

关于编码，本文采用ZIP编码方式，其结构如图2(b)所示.每一对基因分别代表软件构件编号及选中该构件的模块编号，例如，第一对编码表示构件sc2被模块m2选中，同理第二对编码表示sc4被m1选中.这种编码方式除了能较高概率地获得有效方案，而且也满足了约束条件.故而，在每一次交叉和变异之后，算法都无需验证个体是否能令人满意.与经典遗传算法相似的是，2个交叉点也是随机产生的，并且将两个父基因在交叉点处互换部分的染色体.然而，本文中的交叉点必须在染色体的相同位置.

变异可以发生在染色体的任意位置.一对基因由随机生成的构件和模块替换.交叉和变异后，需在个体上做一个有效性测试，以确保构件与模块的结合是有效的.若无效，则放弃该解决方案，而新的个体将会被创建直至通过有效性测试.

3 案例研究

为验证构件优化选择模型的有效性，本节以一个小型金融系统的CBD开发为例，阐述优化选择模型的整个应用流程并对结果进行分析.该系统由10个功能需求构成，开发团队经过分析讨论将其分为Business(m1)、Security(m2)和Assistant(m3)三个模块.从构件市场上选取了20个商业构件(sc1～sc20)进入可选集(s1～s10).表2列出了10个功能需求及由20个商业构件组成的10个构件可选集，并且列出了每个商业构件对于系统不同模块的功能性评级.功能性评级表示构件之于不同功能需求对软件系统模块的功能贡献率程度.1代表对系统功能贡献非常大，0代表对系统无功能贡献.功能性评级的数值大小由开发团队根据商业构件特点共同讨论决定.

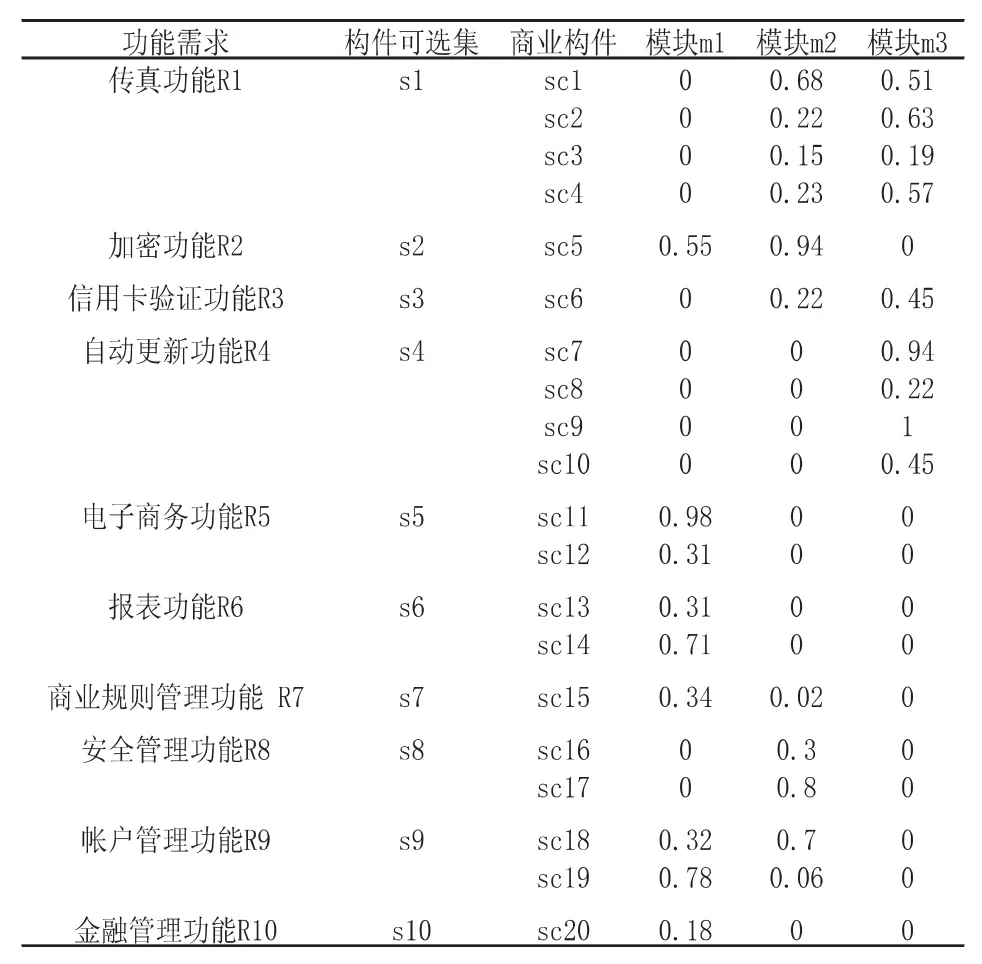
表2 商业构件的功能性评级表

表3列出了软件构件间的交互性评级，取值范围为1～10.交互性评级也是由开发团队根据系统分析讨论确定的.根据上一节给定的优化选择模型，可以计算出Fmax、Fmin、I-max、Imin如下所示：

表3 软件构件间的交互数

在这个案例分析中，取功能性和ICD的权值wf、wl都为0.5，而模块ICD的门限值H设为0.这样根据上一节构建的构件优化选择模型，即公式组(12).基于遗传算法，设定种群规模为50，变异率为0.08，交叉点为1.

基于遗传算法解决优化问题的结果如图4所示，图中的小方点表示每一代适应度的平均值，而小菱形点代表每一代适应度的最大值.可以看到，大概在第12代之后，适应度的值基本趋于稳定并且达到了最优解.对于不同的门限值H，我们又重新用遗传算法求解，表4列出了不同H值所获得的构件选择方案，从表中数据我们可以看到，虽然增加H的值可以提高系统的可维护性，但系统的功能性却呈现非线性的变动.

图4 遗传算法解决优选问题的结果

表4 不同H值的构件选择结果

例如，若开发团队将H的值设为第2项，则第3至第7种方案是可以考虑的，至于选择哪一种方案，得由开发团队结合多个条件综合考虑，比如优先级，比如客户的期望值.若客户认为可维护性于他们而言更加重要，则相比之下，第7种选择方案更适合.相反，若客户希望系统有较高的功能性，则可以考虑第5种选择方案.

实践证明，若问题域是一个较小规模的系统或门限值H设定得过大，则种群规模的设置就显得尤为重要.门限值H需慎重选定，否则很难取得合适的种群来生成最终可行的方案.

4 结束语

基于构件的开发通过集成现有的商业构件来构建新的软件系统,不仅大大提高了软件开发质量和开发效率，而且在分布、开放、动态的Internet计算环境下,可以充分利用网络节点中的大量经实践检验的构件,降低开发成本.本文基于商业构件之于系统的内聚性、耦合度和功能性评级三个考量因子，提出了一种构件优化选择的公式化数学模型，试图调和最大内聚性、最小耦合度、最大功能性之间的平衡关系，通过遗传算法解决优化选择和进化问题，找出最佳的、最合适的解决方案.但该模型仍然需要依赖一些人为的判断，比如功能性评级和交互性评级都需要通过开发团队的分析探讨来确定.故下一步的工作可以引入模糊理论来解决需要主观判定的数据，也可以引入信息理论和复杂度理论来测量系统的内聚性和耦合度.

〔1〕Szyperski,C.,Gruntz,D.,&Murer,S.(2004).Component software:Beyond object-oriented programming. Addison-W esley Professional.

〔2〕Szyperski,C.,&P?ster,C.(1996).Component-oriented programm ing:WCOP’96 workshop report.Special issues in object-oriented programm ing.In W orkshop reader of the 10th European conference on object-oriented programm ing(pp.127–130).

〔3〕Stevens,W.,M yers,G.,&Constantine,L.(1974). Structured design.IBM Systems Journal,13(2),115–139.

〔4〕Parsa,S.,&Bushehrian,O.(2004).A framework to investigate and evaluate genetic clustering algorithms for automatic modularization of software systems.Lecture Notes in Computer Science,699–702.

〔5〕Sarkar,S.,Kak,A.C.,&Nagaraja,N.S.(2005).Metrics for analyzing module interactions in large software systems.In Proceedings of the 12th Asia Pacific software engineering conference(pp.264–271).

〔6〕Sarkar,S.,Rama,G.M.,&Kak,A.C.(2007).API-based and information-theoretic metrics for measuring the quality of software modularization.IEEE Transactions on Software Engineering,33(1),14–32.

〔7〕Abreu,F.B.,&Goul?o,M.(2001).Coupling and cohesion as modularization drivers:Are we being overpersuaded.In Proceedings of the?fth European conference on software maintenance and reengineering. W ashington,DC,USA:IEEE Computer Society.

〔8〕原欣伟,覃正,蔡俊.COTS软构件选择决策模型研究[J].计算机工程，2006,32(11):69-71.

〔9〕王怀军,李军怀,张璟,楼文晓.基于线性规划的构件优选机制研究[J].西安理工大学学报，2010,2(2):186-191.

〔10〕Marian,R.M.,Luong,L.,&Abhary,K.(2006).A genetic algorithm for the optim isation of assembly sequences.Computers&Industrial Engineering,50(4),503–527.

TP311

A

1673-260X（2013）12-0013-04

国家自然科学基金资助项目(No.60963007)，福建省教育厅科技项目(No.JB11251)资助