A Homogeneous Linear Estimation Method for System Error in Data Assimilation

WU Wei1), 2), *, WU Zengmao1), GAO Shanhong1), *, and ZHENG Yi1)



A Homogeneous Linear Estimation Method for System Error in Data Assimilation

WU Wei, WU Zengmao, GAO Shanhong, and ZHENG Yi

1),,266003,2),250031,

In this paper, a new bias estimation method is proposed and applied in a regional ensemble Kalman filter (EnKF) based on the Weather Research and Forecasting (WRF) Model. The method is based on a homogeneous linear bias model, and the model bias is estimated using statistics at each assimilation cycle, which is different from the state augmentation methods proposed in previous literatures. The new method provides a good estimation for the model bias of some specific variables, such as sea level pressure (SLP). A series of numerical experiments with EnKF are performed to examine the new method under a severe weather condition. Results show the positive effect of the method on the forecasting of circulation pattern and meso-scale systems, and the reduction of analysis errors. The background error covariance structures of surface variables and the effects of model system bias on EnKF are also studied under the error covariance structures and a new concept ‘correlation scale’ is introduced. However, the new method needs further evaluation with more cases of assimilation.

model bias estimation; data assimilation; ensemble Kalman Filter; WRF

1 Introduction

Most assimilation methods, such as EnKF (Evensen, 1994; Burgers., 1998; Houtekamer and Mitchell, 1998; Evensen, 2003, 2004), usually rely on the hypothesis that both model error and observational error have a Gaussian distribution, and that the background random error can be reduced in the sense of maximum likelihood. However, in reality, this hypothesis is always violated be- cause errors in both models and observations are often sys- tematic rather than random. The bias naturally introduced into observation increment in assimilation process can degrade the quality of data assimilation, and even results in large flow pattern adjustment (Keppenne., 2005).

A considerable amount of work has been conducted on bias estimation and ‘bias-aware’ assimilation methods (Dee, 2005). The bias estimation algorithms can be classified into two types. One type is the ‘offline’ estimation,the bias is predetermined based on statistics. In the satellite data assimilation operated at the European Centre for Medium-range Weather Forecasts (ECMWF), the observational bias is estimated according to the temporally averaged (about 2 weeks) difference between observational and background values. The problem with the off- line bias estimation method is that parameters have to be manually tuned for changes in detection system, observation operators, and aging of observation sensors. The other type is the ‘online’ estimation (Keppenne., 2005), or the state augmentation method, in which bias is regarded as part of model state and is updated at each assimilation cycle. In the design of an ‘online’ algorithm, a bias model should be formulated based on correct attribution of the bias to particular sources. Keppenne. (2005) assimilated TOPEX/Poseidon altimeter data with the online bias correction EnKF, which has replaced the ‘offline’ method in the operational satellite data assimilation at ECMWF since September 2006.

In the assimilation of high quality in situ sounding data, model errors may be caused by inaccurate surface forcing, poor resolution of the boundary layer, simplified representations of moisture physics and clouds, or various other imperfections (Dee, 2005). Since the forecast error terms are modeled as random vectors, model bias can be regarded as the mean error of a forecast model (Baek., 2006). Baek. (2006) considered three kinds of bias numerical forecast models according to the relationship between attractors of the forecast model and the true system. In one model, they assumed that there exists a transformation from orbits of a forecast model to that of the true system, and also indicated that it is better to let the forecast model follow its own attractor than to force the model state to be close to the truth. Model bias, presenting a challenge for the model development (Dee, 2005), is commonly assumed constant or simple in evolution, and its uncertainty is usually assumed to be uncorrelated with the forecast model state (Dee and Todling, 2000; Bell, 2004; Dee, 2005; Keppenne., 2005).

However, in numerical weather forecast, the bias related to physics schemes may evolve with the flow pattern. The hypothesis of the slow evolvement is no longer valid. In addition, the ‘online’ method needs a number of assim- ilation cycles to approach a convergent value (Baek., 2006). Thus the state augment method is not computa- tionally efficient for the regional forecast and much research work needs to be done for the model bias estimation. In this paper, a new bias model and a bias estimation method are introduced. The methodology is presented in Section 2. A case experiment and results are analyzed in Section 3, and discussion and conclusions are given in the final section.

2 A Model Bias Estimation Method

2.1 Physical Background and Motivation

An EnKF, used in data assimilation here, can be briefly described with the same notation as that used in Evensen (2003):

, (2)

, (3)

. (5)

In the equations above,andare the variables of model state and observation, respectively;denotes the error for the observation;is the observation operator;is the Kalman gain matrix;the covariance matrices for model forecast, analysis and observations are denoted byP,xand, respectively; and(=1, 2, …, N) is the number of ensemble members.

If the attractor determined by model dynamics,. the true model state is represented by x, and real atmosphere state is represented by, model bias=x−x, andd=d+d, wheredis real observations,dis the observation computed from true model state, which is called model observation in this paper, anddis model bias corre- sponding to observations. In most geophysical fluid cases, it might be desirable to let the forecast model state be its own attractor, as proposed by Baek(2006). Therefore, the model observation should be used instead of real observations, and the observation increment should bed−H(). Otherwise, ifthe real observation is assimilated,Kdwill be the erroneous increment caused by model bias.

With respect to a specified variable, the correlation between any two points in a model domain can be calculated from ensemble model fields. By taking any grid point as a reference, a three dimensional (3-D) covariance field of the specified variable can be obtained, defined as ‘covariance field’. Covariance fields of the specified variable change with different reference points. However, their characteristic space scales, defined as ‘correlation scale’ here, do not change. Different variables have their own correlation scale, which is an important parameter to study the characteristics of a covariance matrix.

Once one observation is assimilated and the observation point is taken as a reference, the background field will gain increment with the similar structure to the covariance fields. The erroneous increments caused by bias also has similar structure. For variables with different correlation scales, bias has different effects on the analysis. If one observation variable has a large correlation scale and the observations come from a region with nearly homogenous correlation, model bias at each observation point will result in erroneous increment with similar structure. Furthermore, the amplitude of erroneous increment is positively proportional to the number of observations, and large number of observations will lead to a large error increment, which may alter the flow pattern. Ideally, the bias should be eliminated from observation increment, especially for the element with a large correlation scale.

2.2 Formulation

In reality, it is difficult to obtain exact values of model bias and observation. However, those values can be estimated under some hypothesis. For example, linear function can be a good approximation of the relationship between model bias and background for variables, such as SLP, surface wind, temperature, dew temperature. A large part of model bias can be removed with linear correction as done in weather forecast using direct model output (DMO). Because observations can be organized into batches and assimilated sequentially (Houtekamer and Mitchell, 2001), it is feasible to perform model bias elimination for different variables with different bias models. This paper mainly focuses on the homogeneously linear part of model bias, which is a special case for specific variables. It is assumed that true model back- ground observation and real observations have homogeneously linear relationship, and that model bias evolves with changes in flow pattern. Let

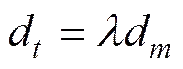
where, because forecast model state is Gaussian and centered around true model state,.,,can be estimated based on the statistics of the real observations and model observations, and updated in every assimilation cycle, as,

. (7)

Using Eqs. (2), (6) and (7), Eq. (3) can be written as

Thus Eq. (8) has a combined property of both ‘online’ (Harris and Kelly, 2001) and ‘offline’ algorithms. The model bias can be computed more easily using statistics rather than the state augmentation method. Compared to the ‘online’ method, the new method does not contain the slow-evolvement hypothesis, reduces number of iterations for bias convergence, and therefore, is more computationally efficient and suitable for regional short range forecasts.

3 Numerical Experiments

3.1 Study Case

In this study, a squall line event occurred in the south Shandong province of China is simulated. Yang(2007) and Zhu(2009) analyzed the synoptic and meso-scale systems of this squall line. As shown in the synoptic charts at 06 UTC 28 April 2006 (Fig.1) from the Global Forecast System analyses (GFS) of the National Center for Environmental Prediction (NCEP), a northeast-southwest (NE-SW)-oriented shallow trough on 500hPa preceded the shear line on 850hPa over the Shandong peninsula. Significant cold advection on 500hPa, a warm advection in lower troposphere, and strong surface heating were favorable conditions for the accumulation of unstable energy over the south Shandong province, where the maximum value of convective available potential energy (CAPE) was greater than 700Jkg. The intrusion of cold air triggered the convection in the northwest Shandong province and generated a squall line, which swept Shandong and Jiangsu provinces and caused great property damage and casualties.

Fig.1 GFS Analysis fields at 06 UTC 28 April 2006. (a) Heights and temperatures (red) at 500hPa, and CAPE (shaded); (b) Stream and temperatures (red) at 850hPa.

3.2 Description of the EnKF System

The regional EnKF data assimilation system is set up with WRF (Version 3.1) and the ensemble square root filter (EnSRF) with 24 members (Whitaker and Hamill, 2002; Evensen, 2004). The WRF integration is performed with 31 η-levels, and 3 nested domains, which have grid sizes of 45, 15 and 3.75km, respectively (Fig.2). The top level of the model is set to 100hPa. Data assimilation is carried out in the largest domain which is used to depict the synoptic flow pattern. The smallest domain is used to catch the characteristics of meso-scale systems. The ensemble covariance is relaxed with a coefficient of 0.6 following Zhang (2004), and no inflation is implemented. To improve the quality of covariance and reduce the long distance spurious correlation resulting from the finite ensemble number, the localization procedure is carried out horizontally using the convolution correlation function proposed in previous studies (Gaspari and Cohn, 1998; Mitchell and Houtekamer, 2000; Hamill., 2001; Mitchell., 2002). The Schur cutoff is set to 2000km, and no vertical localization is implemented for simplicity. To all the ensemble members apply the Betts-Miller-Jan- jic convection scheme (Betts and Miller, 1986), the Mellor-Yamada-Janjic planet boundary layer (PBL) scheme with the Monin-Obukhov surface layer scheme (Mellor and Yamada, 1974, 1982; Janjic, 1994), and the Noah land-surface scheme (Chen and Dudhia, 2001). The difference between ensemble members lies only in their different initial conditions and lateral boundary conditions that are generated based on the GFS data and a new ensemble generation method (see details in the appendix).

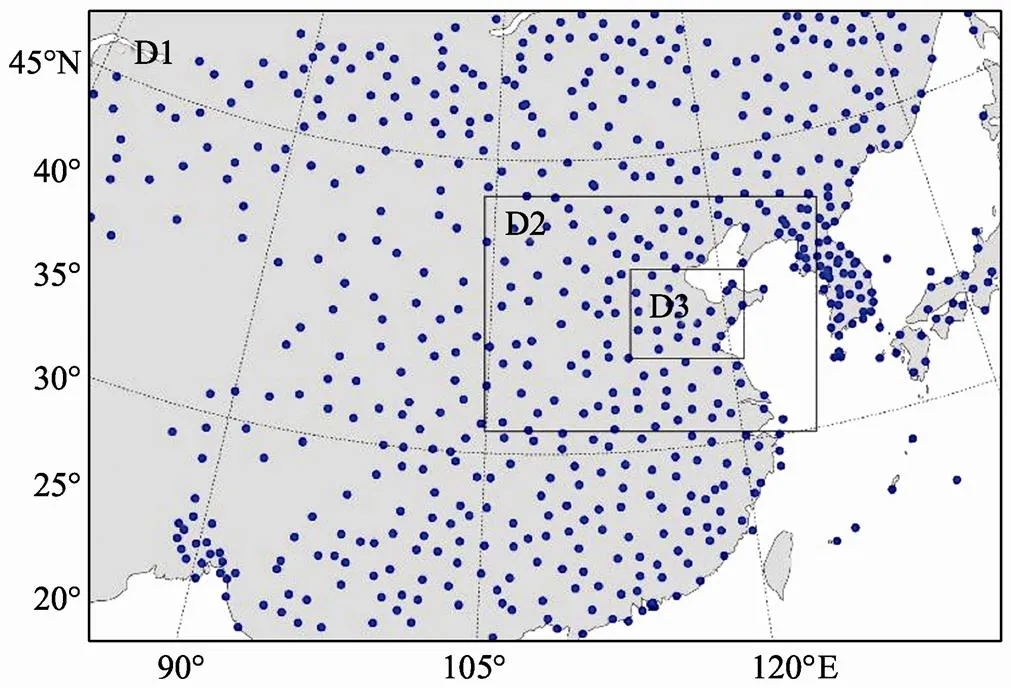
Fig.2 WRF domains and the locations of assimilated observations.

Only observations with 3h intervals from the basic observation stations, which are more reliable, are assimilated. Because the observations within the largest domain unevenly scatters over the 3-ladder topography of landmass, surface observations with the altitude higher than 1500m are excluded to avoid the representative error. The quality of observations is controlled by the criteria similar to, but more strict than those of Torn and Hakim (2008). If the ensemble mean innovation,, is more than 3 times of the standard deviation of the background variance,HPH, the observationis assumed to be erroneous and excluded in the assimilation process.

3.3 Design of Numerical Experiments

The prelude circulation from 12 UTC 27 to 00 UTC 28 April (night at local time,, Beijing Time) is simulated by the EnKF system within the domain D1 only, and surface observations at 18 UTC 27, 21 UTC 27, and 00 UTC 28 April are assimilated to improve the quality of background field. The deterministic forecast is initialized with the ensemble mean as the background field at 00 UTC 28 April. By the interpolation and two-way nesting, the information of in situ observations contained in the ensemble mean of the domain D1 is passed to the two smaller domains.

Besides the controlled forecast experiment without data assimilation, two more experiments with data assimilation are carried out, in which SLP observations at 18 UTC, 21 UTC 27, and 00 UTC 28 April are assimilated. The three experiments are denoted by CTRL, Exp-A and Exp-B, respectively. No model bias correction is implemented in Exp-A, while model bias of SLP is corrected before the data assimilation in Exp-B.

3.4 Results

3.4.1 Distribution of ensemble spread

Figure 3 shows the ensemble spread at the time of 18 UTC 27 April. It is seen that both SLP and 700hPa temperature show higher variance around the frontal area (Fig.1). In North China, a specially concerned region in this study, a high SLP spread center occurs around the low pressure system and its adjacent area with high pressure gradient. From temperatures at 700hPa (Fig.3b), a high spread band is located over the region of the Shandong province and Beijing, which overlays the area with short waves and great temperature gradient. The spread of geo-potential height also gets high value centers around the trough and ridge, and the spread of surface specific humidity gets high value centers at the frontal area (not shown). The close relationship between the distribution of ensemble spread and synoptic system is consistent with the findings by previous studies, demonstrating the validity of the ensemble initialization method developed in this study.

Fig.3 Ensemble mean (solid lines) and ensemble spread(shaded) at 18UTC 27, April 2006. (a) Sea level pressure (hPa); (b) Temperature on 700hPa (℃).

The average vertical profiles of some observed variables are also studied in this section. Opposite to the profiles of specific humidity in PBL, the spread of specific humidity in this case reduces rapidly from the top of planet boundary to surface level and the spread of temperature follows the same trend as that of humidity. Although wind speed increases with height in troposphere, the spread of it shows higher values at the middle and lower levels. As discussed in Section 2, the effect of data assimilation is mainly determined by the ensemble spread, and if the spread of model observations is small, the spurious increment caused by model bias can be much larger, which explains the difficulty in the assimilation of surface air temperature and humidity (Mitchell and Houtekamer, 2000).

3.4.2 Structure of background error covariance

Background error covariance plays a fundamental role in data assimilation. The structure of model error covariance of different variables is studied to examine the impact of bias on data assimilation in detail. The observation site, Beijing (116.4˚E, 39.80˚N), is taken as a reference point and the covariance fields are computed at the location. For simplicity, no localization procedure is implemented. As one of intrinsic advantages of EnKF, the distribution of forecast error covariance evolves with changes in flow patterns during the whole integration period (Meng and Zhang, 2007). In general, the evolution of the structure of error covariance demonstrates the ‘adjustment progress’ and the ‘adaptation process’. After ensembles are initialized, the structure of forecast error covariance adjusts quickly to be compatible with the flow pattern, and then it adapts slowly together with the air flow. At the initial stage of the ensembles, the long-dis- tance spurious correlation related to limited number of ensembles is large, but it decreases significantly as the integration goes on.

At 12 UTC 27 April, the error covariance of SLP has a structure of synoptic scale or meso-scale (Fig.4). After 6 hours of adjustment, the error covariance shows a large scale space distribution, and it seems that for a large part of model domain, SLP at different locations are highly positively correlated with that at the reference point. At 00 UTC 28 April, the entire domain D1 shows high positive correlations. The great changes of scale in SLP error covariance do not show up for other variables, such as surface temperature and humidity at the 2 m level (T2, Q2) and surface wind at the 10m level (two components denoted by U10 and V10). The large scale of forecast error covariance indicates that each SLP observation has broad representative characteristics, and assimilation of it affects a large area in the model domain. Therefore, the SLP observation increment−should have high accuracy. As discussed in section 2, large number of SLP observations will lead to enormous erroneous increment if bias exists. Furthermore, as the average spatial distance of the surface observation network is much smaller than that of the SLP error covariance, ‘saturation’ may occurs in the SLP assimilation (Anderson., 2005). Different from SLP, the spatial scale of the horizontal covariance of four other surface variables, T2, Q2, U10 and V10, does not change much with the integration, though their structures are adjusted to flow (Fig.5). Because the four surface variables have smaller correlation scales, the information contained in these observations has a limited space of effectiveness. Therefore, to effectively improve the quality of modeled fields, observations of these four variables should have larger spatial density than that of SLP. The characteristics of the spatial scales of surface variables’ covariance distribution can provide us with an approach to the design of an optical observation network.

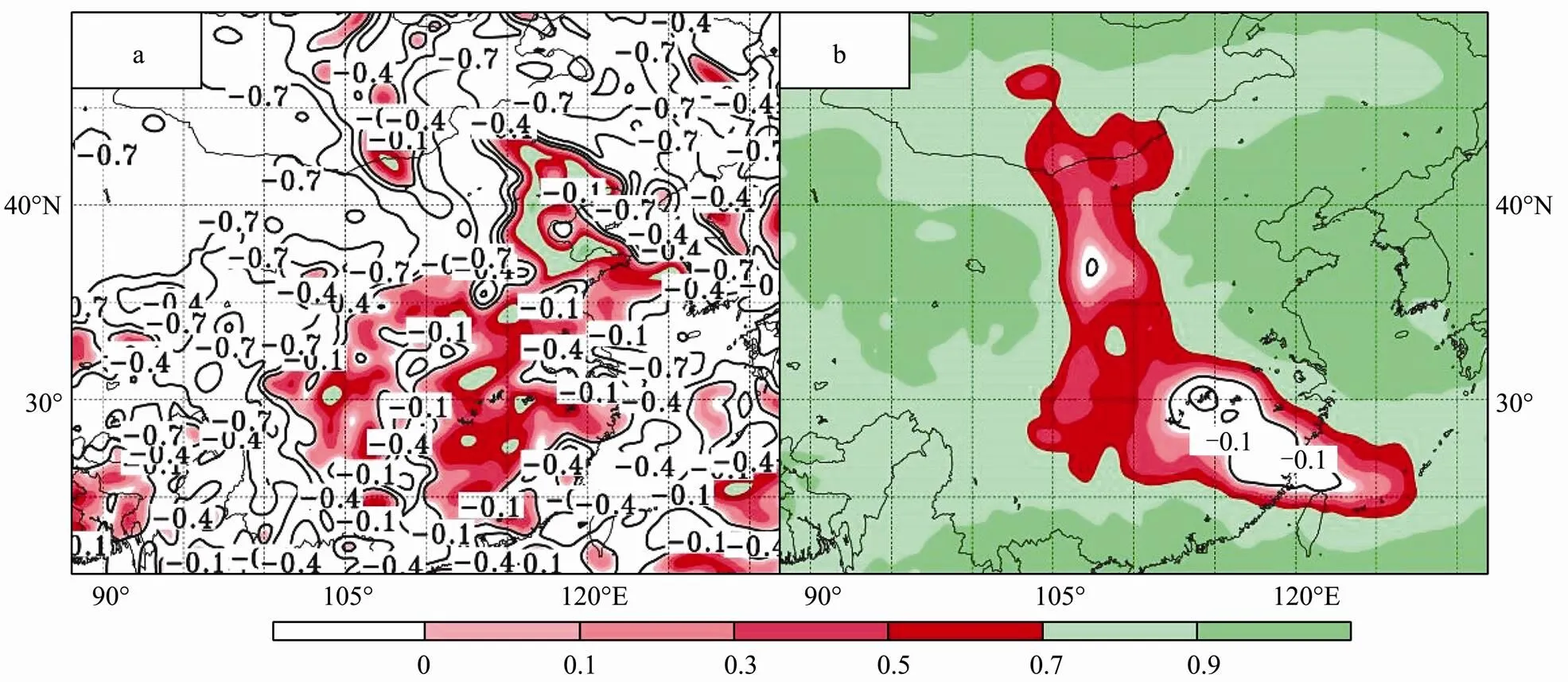
Fig.4 Forecast error correlation of SLP at 12 UTC 27 April (a) and 18 UTC 27 April (b). Shaded area represents positive correlation and contoured area negative correlation.

Fig.5 Same as in Fig.4, but for forecast error correlation of surface specific humidity.

The average coefficient profiles between surface variables and variables at high levels are calculated to study the propagation of surface observation information to the model space. In general, the average covariance of a model variable between surface and other vertical levels decreases with height. Between surface and high levels, different model variables tend to have little covariance except for the covariance of surface temperature correlated with geo-potential height. The coefficient profiles have significant diurnal changes within boundary layer. During daytime, strong vertical mixing in boundary layer can result in close correlation between variables at different levels. However, the correlation between surface variables and variables at different levels sharply reduces during night time.

Though the structure of error covariance may be dif-ferent under different model settings, such as domain size, spatial resolution and physics schemes used, the conclusions drawn in this section might be broadly valid.

3.4.3 Comparisons of SLP assimilation experiments

Analyzed fields of both Exp-A and Exp-B at 00 UTC 28 April are compared in the followings.

First, the GFS analyzed field at 00 UTC 28 April is taken as the ‘real state’ for the verification of circulation pattern. In general, the analyzed error of geo-potential height in Exp-B is smaller than that in Exp-A (Fig.6), except over north China, where the amplitude of a short wave seen in Exp-B is a little larger than that in Exp-A. As for temperature, the effect of model bias correction is significant. The isothermal contours, as well as surface humidity, in Exp-B are much closer to GFS’ results than in Exp-A. The results demonstrate that circulation pattern can be improved if model bias correction is implemented through SLP data assimilation.

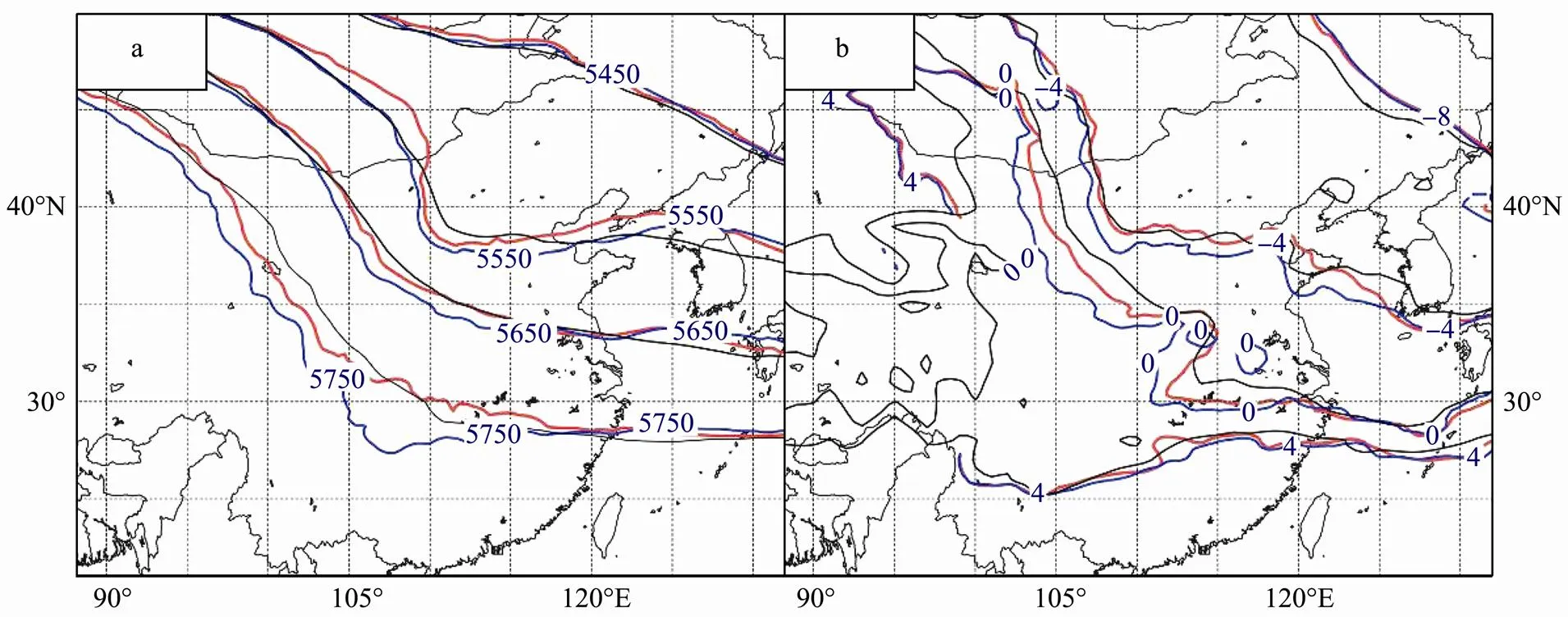
Fig.6 Circulation at 00 UTC 28 Aprilof Exp-A (blue), Exp-B (red) and GFS analysis(black). (a) geo-potential heights on 500hPa; (b) temperatures on 700hPa.

Second, surface observations and sounding data are taken as the ‘real atmosphere state’. Table 1 shows that the analysis error of Exp-B is less than that of Exp-A in general. Bias correction contributes to significant reduction of SLP analysis error, and the error of surface temperature is reduced by 5.1%. Little reduction is showed for the analyzed error of x-directional wind speed, and the error increases for the y-directional wind speed.

Table 1 Comparisons of analysis errors and ensemble spreads of Exp-A and Exp-B

Notes: T2, surface temperature at 2 m height; U10 and V10, surface wind speeds at 10m height forandcomponents, respectively.

Using the sounding data at 00 UTC 28 April as reference, the spread of ensemble is smaller than analysis errors of all variables (Fig.7). Dirren. (2007) indicated that this imbalance may be due to a single variable assimilation. The spread of geo-potential height is close to analysis error, and the balance is maintained especially in low troposphere, which demonstrates that the low level geo-potential height can be significantly improved through the SLP data. Because temperature and wind observations are not assimilated with the assimilation of SLP data, the corresponding spreads greatly decrease with forecasting time (not shown). The analyzed error of temperature reduces with height under 700hPa, but those of geo-potential height and wind increase with height. This is in accordance with Houtekamer.’s (2005) statement that in middle and lower troposphere, the error growth rate of ensemble mean is greater than that of perturbation; however, in higher troposphere near the top of model space, weakening perturbation results in the underestimate of fast growing error.

Fig.7 Average profiles of analysis error of Exp-A (thin line) and Exp-B (thick line) and ensemble spread(broken line) on sites of radio sounding at 00 UTC 28 April. (a) geo-potential height; (b) temperature; (c) x-component wind (U); (d) y-component wind (V).

Fig.8 Calculated maximum radar echo (>=30dbz only) at 09 UTC 28 April. Shaded area is the results of Exp-A and red line is the results of Exp-B in (a); red line is the results of Exp-CTRL and streams are the results of the objective analysis of surface winds in (b).

Fig.9 (a) Surface wind vectors and (b) streams at 03 UTC 28 April. Blue line is for Exp-A and red line for Exp-B in (a);red line is for objective analysis and blue line for Exp-CTRL in (b).

In general, EnKF with model bias correction produces higher quality analysis than that without bias correction. Among the different variables, the analysis error of geo-potential height reduces most significantly. On levels below 700hPa, the results of Exp-B show that the spread of geo-potential height is in good accordance with the analyzed error that is reduced effectively with bias correction.

Third, to further verify the effect of SLP data assim- ilation, the analysis fields at 00 UTC 28 are used as the initial condition to simulate the evolution of meso-scale systems during the daytime of 28 April. The maximum radar echo is computed within the domain D3 for the depiction of convective systems. In Exp-B, the small scattered convection system first occurs in the central part of Shandong province, slightly earlier than that in Exp-CRTL, but later than the real state (Fig.8). The delay of convection may be the result of a stable vertical structure in the forecast. The surface temperature in these experiments is relatively lower compared to the observations. In the forecast, the squall line moves across the boundary between Shandong and Jiangsu provinces with a slower speed in Exp-B than in Exp-CTRL, which is consistent with the observations. By the comparison of the forecasted surface wind field at 03 UTC 28 April, it is found that the surface flow pattern and the cold frontal position are significantly improved in Exp-B (Fig.9), which is important for the accurate forecast of the convection system. The correction of model bias also has significant effects on the forecast of meso-scale systems. Therefore, the assimilation of SLP significantly improves the squall line forecast.

4 Summary

This paper proposes a new homogeneous linear estimation method to study the impact of model system error on an EnKF. Through modeling a severe weather event caused by a squall line, the forecast error covariance structure of different variables and the roles those variables play in the EnKF are examined. The homogeneous linear error correction method is also demonstrated in the data assimilation experiment. The new method has significant effects on circulation and meso-scale system forecasting, and the reduction of the analysis errors.

A new concept, ‘correlation scale’, is introduced in this paper. For variables with larger correlation scale, such as sea level pressure, model bias can greatly degrades the quality of data assimilation, with the result that the more SLP observations are assimilated, the more errors can be introduced into analysis field. The erroneous gain of a variable has a similar structure to its forecast error covariance. The forecast error covariance scale can be regarded as the effective radius of observations, and can be used to determine the suitability of observation density. The study indicates that the scale of forecast error covariance of sea level pressure is much greater than the average scales of other variables such as surface temperature and humidity, and that the assimilation of SLP observations will result in the problem of ‘saturation’.

Associated with the boundary layer physics, humidity and temperature tend to have small ensemble spread in the boundary layer. It may be problematic in data assimilation, especially when model bias exists. The averaged vertical covariance profile in boundary layer often has a significant diurnal cycle over land.

Undoubtedly, further researches need to be done in the assimilation of surface observations. The adaptation process of error covariance structure also needs further study. As forecast leading time increases, the contribution of assimilation to forecast skill will decrease gradually. For example, the effect of assimilated surface wind may diminish quickly under stable flow pattern (Chou, 2007). However, because low level wind field plays an important role in triggering convection, further investigation is needed for the assimilation of wind observations.

Acknowledgements

This research is supported by the Provincial Science and Technology Development Program of Shandong under Grant No. 2008GG10008001; Key Technology Integration and Application Program of China Meteorological Administration, under Grant No. CMAGJ2011M32; Fore- caster Research Program of China Meteorological Administration, under Grant No. CMAYBY2012-031; Science and Technology Research Programs of Shandong Provincial Meteorological Bureau, under Grant Nos. 2012sdqxz03, 2012sdqxz01, 2010sdqxz01. The development of the EnKF system got help from http://enkf.nersc.no/ provided by Geir Evensen. The authors also wish to thank NCAR for providing the WRF model system.

Appendix

The Ensemble Generation Method

To get the best ensemble forecast results, the initial ensemble should mostly contain the fast-growing modes and produce a good estimation of the subspace of fast growing perturbations (Ehrendorfer and Tribbia, 1997; Toth and Kalnay, 1997; Wei2006). In order to prevent the loss of difference and to keep the ensemble variance in the domain where the data assimilation is carried out (Dowell., 2004; Fujita, 2007), more efforts need to be made in a limited area ensemble forecast than in a global ensemble forecast (Ehrendorfer and Errico, 1995; Houtekamer, 1995; Houtekamer and Derome, 1995; Anderson, 1997; Ehrendorfer and Tribbia, 1997; Toth and Kalnay, 1997; Fisher, 2001). As in some previous researches (Nutter., 2004a, b; Torn., 2006), the ensemble lateral conditions are also provided to ensemble members in this study.

Without the global ensemble background, the generation of limited area ensemble will be difficult. Several methods have been proposed, such as GEV (global ensemble values), CTS (climatology time series) (Torn, 2006; Dirren, 2007), GES (global ensemble sampling), LAES (limited-area ensemble sampling), FCP (fixed covariance perturbations). Compared with these ensemble generation methods, the present method has the following advantages: 1) the lateral conditions contain the main error pattern in a region, 2) the initial ensemble perturbation is adapted for the flow pattern, 3) similar amplitude is created as the background error, and 4) it has less computational cost. The followings are the implementation procedures of the method:

Step 1: Leading typical fields of the GFS 24h forecast error, covering the main error spaces, are computed and are combined to generate a number of random orthogonal perturbations (the number is 12 in this paper), which is further resized according to the GFS 700hPa temperature with 6h forecast error in the sense of mean square root. These perturbations are added to the analyzed GFS fields in pairs (negative and positive) with the increasing coefficient according to GFS forecast leading time. Altogether 24 perturbed and one non-perturbed GFS background fields are prepared.

Step 2:After WRF is initialized for each member, the initial perturbation is greatly weakened due to the imbalance between it and the dynamics of first-guessed fields. Therefore the balanced perturbation is increased again in the same way as in Step1. Based on empirical tests, the criteria is determined such that the spread of 700hPa temperature equals one-fifth of its 6 h forecast error.

Step 3: After a 6–12h ensemble integration, the perturbations are adapted by the flow, and the growing perturbations are strengthened and the error spaces are covered. The ensemble perturbations are greatly improved, the spread is similar to the GFS forecasted error, and therefore, the ensemble can be used for the EnKF.

Anderson, J. L., 1997. The impact of dynamical constraints on the selection of initial conditions for ensemble predictions: Low-order perfect model results., 125: 2969-2983.

Anderson, J. L., Wyman, B., Zhang, S. Q., and Hoar, T., 2005. Assimilation of surface pressure observations using an ensemble filter in an idealized global atmospheric prediction system., 62: 2925-2938.

Baek, S. J., Hunt, B. R., Kalnay, E., Ott, E., and Szunyogh, I., 2006. Local ensemble Kalman filtering in the presence of model bias., 58: 293-306.

Bell, M. J., Martin, M. J., and Nichols, N. K., 2004. Assimilation of data into an ocean model with systematic errors near the equator., 130: 873-893.

Betts, A. K., and Miller, M. J., 1986. A new convective adjustment scheme part II: single column tests using GATE wave, BOMEX, ATEX and artic air-mass data sets., 12: 693-709

Burgers, G., Leeuwen, P. J., and Evensen, G., 1998. Analysis scheme in the ensemble Kalman filter., 126: 1719-1724.

Chen, F., and Dudhia, J., 2001. Coupling an advanced land surface hydrology model with the Penn State/NCAR MM5 modeling system. Part 1: Model description and imple- mentation., 129: 569-586.

Chou, J. F., 2007. An innovative road to numerical weather prediction–from initial value problem to inverse problem., 65: 673-682.

Dee, D. P., 2005. Bias and data assimilation., 131: 3323-3343.

Dee, D. P., and Todling, R., 2000. Data assimilation in the presence of forecast bias: the geos moisture analysis., 128: 3268-3282.

Dirren, S., Torn, R. D., and Hakim, G. J., 2007. A data assimilation case study using a limited-area ensemble Kalman filter., 135: 1455-1473.

Dowell, D. C., Zhang, F. Q., Wicker, L. J., Snyder, C., and Crook, N. A., 2004. Wind and temperature retrievals in the 17 may 1981 arcadia, oklahoma, supercell: ensemble Kalman filter experiments., 132: 1982-2005.

Ehrendorfer, M., and Errico, R. M., 1995. Mesoscale predict- ability and the spectrum of optimal perturbations., 52: 3475-3500.

Ehrendorfer, M., and Tribbia, J. J., 1997. Optimal prediction of forecast error covariances through singular vectors., 54: 286-313.

Evensen, G., 1994. Sequential data assimilation with a nonlinear quasi-geostrophic model using Monte Carlo methods to forecast error statistics., 99: 10143-10162.

Evensen, G., 2003. The ensemble kalman filter: Theoretical formulation and practical implementation., 53: 343-367.

Evensen, G., 2004. Sample strategies and square root analysis schemes for EnKF., 54: 539-560.

Fisher, 2001. Assimilation techniques: Approximate Kalman Filters and singular vectors. http://www.ecmwf.int/newsevents/training/lecture_notes/pdf_files/ASSIM/Kalman.pdf.

Fujita, T., Stensrud, D. J., and Dowell, D. C., 2007. Surface data assimilation using an ensemble Kalman filter approach with initial condition and model physics uncertainties., 135: 1846-1868.

Gaspari, G., and Cohn, S. E., 1998. Construction of correlation functions in two and three dimensions.,125: 723-757.

Hamill, T. M., Whitaker, J. S., and Snyder, C., 2001. Distance-dependent filtering of background error covariance estimates in an ensemble Kalman filter., 129: 2776-2790.

Harris, B. A., and Kelly, G., 2001. A satellite radiance-bias correction scheme for data assimilation., 127: 1453-1468.

Houtekamer, P. L., 1995. The construction of optimal pertur- bations., 123: 2888-2898.

Houtekamer, P. L., and Derome, J., 1995. Methods for ensemble prediction., 123: 2181-2196.

Houtekamer, P. L., and Mitchell, H. L., 1998. Data assimilation using an ensemble Kalman filter technique., 126: 796-811.

Houtekamer, P. L., and Mitchell, H. L., 2001. A sequential ensemble Kalman filter for atmospheric data assimilation., 129: 123-137.

Houtekamer, P. L., Mitchell, H. L., Pellerin, G., Buehner, M., Charron, M., Spacek, L., and Hansen, B., 2005. Atmospheric data assimilation with an ensemble Kalman filter: Results with real observations., 133: 604-620.

Janjic, Z. I., 1994: The step-mountain eta coordinate model: Further development of the convection, viscous sublayer, and turbulence closure schemes., 122: 927-945.

Keppenne, C. L., Rienecker, M. M., Kurkowski, N. P., and Adamec, D. A., 2005. Ensemble Kalman filter assimilation of temperature and altimeter data with bias correction and application to seasonal prediction., 12: 491-503.

Mellor, G. L., and Yamada T., 1974: A hierarchy of turbulence closure models for planetary boundary layers., 31: 1791-1806.

Mellor, G. L., and Yamada T., 1982: Development of a turbulence closure model for geophysical fluid problems., 20: 851-875.

Meng, Z., and Zhang, F., 2007. Tests of an ensemble Kalman filter for mesoscale and regional-scale data assimilation. Part II: Imperfect model experiments., 135: 1403-1423.

Mitchell, H. L., and Houtekamer, P. L., 2000. An adaptive ensemble Kalman filter., 128:416-433.

Mitchell, H. L., Houtekamer, P. L., and Pellerin, G., 2002. Ensemble size, balance, and model-error representation in an ensemble Kalman filter., 130: 2791-2808.

Nutter, P., Stensrud, D., and Xue, M., 2004a. Effects of coarsely resolved and temporally interpolated lateral boundary con- ditions on the dispersion of limited-area ensemble forecasts., 132: 2358-2377.

Nutter, P., Xue, M., and Stensrud, D., 2004b. Application of lateral boundary condition perturbations to help restore dis- persion in limited-area ensemble forecasts., 132: 2378-2390.

Torn, R. D., Hakim, G. J., and Snyder, C., 2006. Boundary conditions for limited-area ensemble Kalman filters., 134: 2490-2502.

Torn, R. D., and Hakim, G. J., 2008. Performance characteristics of a pseudo-operational ensemble Kalman filter., 136: 3947-3963.

Toth, Z., and Kalnay, E., 1997. Ensemble forecasting at ncep and the breeding method., 125: 3297-3319.

Wei, M., Toth, Z., Wobus, R., Zhu, Y. J., Bishop, C. H., and Wang, X. G., 2006. Ensemble transform Kalman filter-based ensemble perturbations in an operational global prediction system at NCEP., 58: 28-44.

Whitaker, J. S., and Hamill, T. M., 2002. Ensemble data assim- ilation without perturbed observations., 130: 1913-1924.

Yang, X. X., Li, C. H., Yang, C. F., Tai, Q. G., Chen, Y. K., and Zhou, X. S., 2007. Analysis of a squall line event on 28 April 2006 in Shandong province., 33: 74-81.

Zhang, F., Snyder, C., and Sun, J., 2004. Impacts of initial estimate and observation availability on convective-scale data assimilation with an ensemble Kalman filter., 132: 1238-1253.

Zhu, L. L., Wu, Z. M., Tai, Q. G., Wu, W., and Zhang, J. Y., 2009. Analysis of gravity wave characteristics of a strong squall line process in April 2006 in Shandong province., 25: 465-474.

(Edited by Xie Jun)

10.1007/s11802-013-1918-1

ISSN 1672-5182, 2013 12 (3): 335-344

. E-mail: wuwei_sd@163.com E-mail: gaosh@ouc.edu.cn

(December 12, 2011; revised January 31, 2012; accepted November 26, 2012)

© Ocean University of China, Science Press and Springer-Verlag Berlin Heidelberg 2013