联合采用高通低通滤波与Hilbert-黄变换的非线性信号分析

张 璨，文福拴，王建军，刘焕磊

(1.浙江大学 电气工程学院，浙江 杭州310027;2.山西省电力公司 长治供电分公司，山西 长治046011)

0 引 言

中国台湾中央大学的黄锷教授(Norden E.Huang)在美国航空暨太空总署 (The National Aeronautics and Space Administration，NASA)工作期间提出了一种新的时间序列信号分析方法，即著名的Hilbert-黄变换(Hilbert-Huang Transform，HHT)［1，2］。HHT是对以傅里叶变换为基础的线性和稳态谱分析的一个重大突破，可以对非线性非平稳信号进行分析［3］。HHT 包含两个过程:a.通过经验模态分解 (empirical mode decomposition，EMD)将信号分解成有限个本征模态函数(intrinsic mode function，IMF)分量;b.对IMF进行Hilbert 变换得到瞬时频率和瞬时幅值。EMD是HHT 的核心过程，因为只有对经过EMD 之后的IMF 进行Hilbert 变换，得到的瞬时频率和瞬时幅值才具有物理意义［4］。然而，在实际应用时EMD 存在模态混叠问题，即当信号中的2 个组成分量的频率在2 倍频内时，EMD 无法将其分解开［5，6］。为提高EMD 的频率分辨率，解决2 倍频内不可分的问题，有些学者已经做了一些研究工作。例如，文献［7］ 提出了掩蔽信号EMD 法，通过采用比最高频率分量频率更高的掩蔽信号将该高频分量分离出来，这在一定程度上解决了常规EMD 方法无法分离2 倍频分量的问题，但并未给出如何系统地选取掩蔽信号方法;文献［8］提出了利用快速傅里叶变换构造掩蔽信号的方法;文献［9］ 提出了基于快速傅里叶变换和信号能量的掩蔽信号构造方法，较好的解决了文献［7］ 中的方法不能有效分解低频信号的问题;文献［10］ 提出了频率外差EMD 方法，通过频率外差将高低频信号翻转，从而扩大了高频和低频信号间的差距，进而可采用常规EMD 方法分解，但由于EMD 分解的误差和边界效应会导致在低频段产生伪模态分量，经频率外差后这些伪模态分量将翻转为高频分量，与真实高频分量混在一起而难以分辨。文献［11，12］ 通过改进外差频率选择方法使得信号中各组成分量的频率只发生偏移而不翻转，这就避免了伪模态分量翻转为高频分量的问题。

针对EMD 的模态混叠问题，现有的研究工作大多集中于改进掩蔽信号EMD 方法和频率外差EMD 方法，而很少有采用滤波方法来解决这一问题;对于是否发生模态混叠通常只是基于EMD 分解得到的各IMF 图来直观判断，缺乏量化指标。

在上述背景下，本文将HHT 应用于非线性信号分析之中，并研究了EMD 模态混叠问题的解决方法。首先，通过对非线性信号采用HHT 瞬时频率图分析，判断是否发生模态混叠。之后，对于发生模态混叠的部分利用傅里叶变换确定发生模态混叠的信号频率，并将高通低通滤波与HHT 结合，较好的解决了EMD 无法对2 倍频内信号分解的问题。最后，用算例说明了所提方法的有效性。

1 Hilbert-黄变换

1.1 经验模态分解 (EMD)

EMD 将信号分解为具有不同尺度特征的本征模态函数(IMF)分量，这些IMF 分量满足以下两个条件［7］:

(1)极值点个数和过零点个数相等或者最多相差1;

(2)在任意时刻，由极大值和极小值构成的上下包络线的平均值为0。

对于任意信号S(t)，将其分解为各本征模态函数分量的步骤如下［1，3，7］:

(1)对所有局部最大值点做3 次样条插值，形成上包络线;

(2)对所有局部最小值点做3 次样条插值，形成下包络线;

(3)计算上下包络线的平均值曲线M1(t)，则信号S(t)与M1(t)之差即为P1(t):

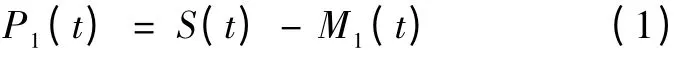
(4)如果P1(t)满足上述IMF 的两个条件，则其为第一个IMF，否则将其作为原始信号重复步骤(1)到步骤(3)，得到P11(t):

式中:M11(t)为P1(t)的上下包络线均值。

(5)重复筛选直到第k 次筛选时由式(3)得到的P1k(t)满足IMF 的两个条件:

在实际计算时，可利用由式(4)求得的VD值判断每次筛选结果是否为IMF:

式中:r 为信号采样点数;VD的值通常在0.2 ～0.3之间。

(6)令C1(t)= P1k(t)，则C1(t)即为第一个IMF，其包含了原信号中周期最短的分量。将C1(t)从S(t)中分离出来:

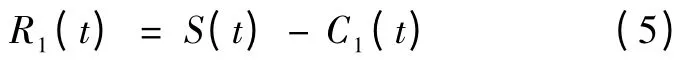
(7)将R1(t)作为原始信号重复以上步骤n次，可获得信号S(t)的n 个IMF:

(8)当Rn为单调函数而不能从中再分解出IMF 时，分解过程结束。最后可以得到:

1.2 Hilbert 变换

对经过EMD 得到的各IMF 进行Hilbert 变换［1，3，7］。定义C(t)的Hilbert 形式为

构造解析信号

幅值函数为

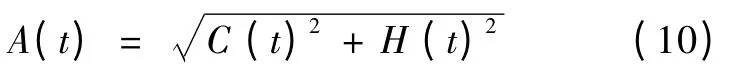
瞬时相位为

瞬时频率为

2 采用HHT 的非线性信号分析

2.1 EMD 模态混叠评判指标

采用HHT 分析非线性信号，若不存在模态混叠则可直接得到各次组成分量的信息;否则，就需要采取进一步的措施。对于是否发生模态混叠，目前常用的方法是通过EMD 分解得到的各IMF 图直观判断，缺乏量化指标。有鉴于此，这里提出一种通过HHT 瞬时频率判断是否发生模态混叠的指标。定义频率落差为

式中:fl和fr-m 分别为HHT 瞬时频率图中第l 个和第r-m 个频率点。由于EMD 存在边界效应，所以在式 (13)中求取最大值和最小值时去除了边界的部分点。

用dset表示阈值，则可通过下式判断是否发生模态混叠:

dset由专家根据所分析的具体信号以及对误差的容忍情况来确定。当某个本征模态函数分量的瞬时频率不满足式 (14)时，则判定存在模态混叠，需采取措施消除。

2.2 基于高通低通滤波的EMD

可以首先采用傅里叶变换确定信号中的组成分量，之后应用高通低通滤波将位于2 倍频内的高频信号和低频信号分别分离出来，最后采用EMD 方法对分离开的信号进行分解。

假设对发生模态混叠的信号X(t)采用傅里叶变换后确定的各组成分量的频率为fa，fb和fc(fa＜fb＜fc)，且fc/fb＜2，fb/fa＞2。由于fb和fc的频率位于2 倍频内，所以采用EMD 时会发生模态混叠。采用高通低通滤波可得到如下2 个信号:

式中:FH(·)和FL(·)分别为高通滤波变换和低通滤波变换。

频率为fc的分量位于XH(t)中，频率为fa和fb的分量位于XL(t)中。对XH(t)和XL(t)采用EMD 方法就不会发生模态混叠。

2.3 非线性信号分析步骤

采用HHT 分析非线性信号的步骤如下:

(1)对所要分析的信号采用HHT 得到各模态分量的瞬时频率图;

(2)计算各模态分量的频率落差，找到开始发生模态混叠的模态函数分量;

(3)从原始信号中去除发生模态混叠之前的各个分量，得到分析信号;

(4)对分析信号进行傅里叶变换，并对位于2 倍频内的分量分别进行高通和低通滤波;

(5)对滤波后的信号采用HHT 得到各模态分量图及其瞬时频率图和瞬时幅值图;

(6)将步骤(5)中的分量与步骤(2)中未发生模态混叠的分量整合，得到完整的信号各模态函数分量。

采用HHT 分析非线性信号的流程如图1所示。

3 算例分析

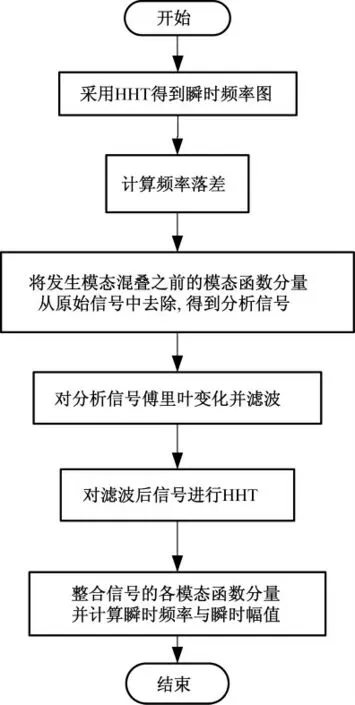
图1 采用HHT 分析非线性信号的流程Fig.1 The flowchart of the HHT based nonlinear signal analysis

为验证所提方法的有效性，本节给出算例结果。假设信号 S (t)= 10 sin (2π50t)+ 5 sin(2π100t)+4 sin (2π150t)+6 sin(2π350t)，dset=50 Hz。首先利用常规EMD 方法对原始信号s(t)进行分解，得到各IMF 的结果如图2 所示，IMF 的瞬时频率如图3 所示。

从图2 的EMD 分解结果中可直观看出IMF2发生了模态混叠。由图3 可得到前2 个IMF 的频率落差，即 df1= 28 Hz，df2= 84 Hz;由式(14)可判断出从第2 个IMF 开始出现模态混叠。从原始信号S(t)中除去IMF1 后可得到分析信号X(t)。对X(t)进行傅里叶变换，可得到图4所示的结果。

从图4 可看出X(t)中包含了150 Hz，100 Hz和50 Hz 这3 个分量，150 Hz 与100 Hz 以及100 Hz与50 Hz 位于2 倍频内，这就解释了图2中IMF 发生模态混叠的原因。对X(t)经过高通低通滤波后再采用EMD 方法分解，并与图2 中未发生模态混叠的分量整合，结果如图5 所示。各IMF 的瞬时频率和瞬时幅值分别如图6 和图7所示，端点处的异常是由滤波器的延迟造成的。从图5 ～图7 可看出采用所提方法可有效解决模态混叠问题，最后所得到的结果与原始信号S(t)一致。

图2 采用常规EMD 方法对信号的分解结果Fig.2 Signal decomposition results by the conventional EMD method

图3 各IMF 的瞬时频率Fig.3 The instantaneous frequency of each IMF

图4 X(t)的傅里叶谱分析Fig.4 Fourier spectrum analysis results of X(t)

4 结 论

在对Hilbert －黄变换的基本原理和存在问题进行分析的基础上，提出了基于HHT 瞬时频率来判断是否发生模态混叠的指标。之后，通过顺序采用傅里叶变换和高通低通滤波这两种方法，来解决常规经验模态分析方法无法分解2 倍频内信号的问题。将滤波后再采用EMD 获得的各模态函数分量与之前未发生模态混叠的分量整合，获得了原始信号完整的各模态函数分量及相应的频率和幅值。最后，用算例说明了所提方法的正确性。

图5 滤波后EMD 分解结果Fig.5 The signal decomposition results by employing the EMD method after filtering

图6 滤波后应用HHT 得到的各IMF 的瞬时频率Fig.6 The instantaneous frequency of the IMF by applying the HHT after filtering

图7 滤波后应用HHT 得到的各IMF 的瞬时幅值Fig.7 The instantaneous amplitude of the IMF by applying the HHT after filtering

［1］Huang N E，Shen Z，Long S R，et al.The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis［J］.Proceedings of the Royal Society of London Series A，1998，45(4):903 －995.

［2］Huang N E，Shen Z，Long S R.A new view of non-linear water waves:the Hilbert spectrum［J］.Annual Review of Fluid Mechanics，1999，31(1):417 －457.

［3］苏玉香，刘志刚，李科亮，等.Hilbert-Huang 变换在电气化铁路谐波检测中的应用［J］.电网技术，2008，32(18):30 －35.

［4］胡维平，莫家玲，杜明辉.经验模态分解中的频域分辨率及其改进方法［J］.华南理工大学学报(自然科学版)，2007，35(5):15 －19.

［5］李成鑫，刘俊勇，杨嘉湜，等.移频经验模态分解在低频振荡参数提取中的应用［J］.电力系统自动化，2011，35(20):1 －6.

［6］杨德昌，REHTANZ C，李 勇，等.基于改进希尔伯特－黄变换算法的电力系统低频振荡分析［J］.中国电机工程学报，2011，31(10):102 －108.

［7］Deering R，Kaiser J F.The use of a masking signal to improve empirical mode decomposition［C］// Proceedings of IEEE International Conference on Acoustic，Speech，and Signal Processing.NC，USA:Durham，2005:485 －488.

［8］Senroy N，Suryanarayanan S，Ribeiro P F.An improved Hilbert-Huang method for analysis of time-varying waveforms in power quality ［J］.IEEE Trans on Power Systems，2007，22(4):1843 －1850.

［9］Laila D S，Messina A R，Pal B C.A refined Hilbert-Huang transform with applications to interarea oscillation monitoring［J］.IEEE Trans on Power Systems，2009，24(2):610 －620.

［10］Senroy N，Suryanarayanan S.Two techniques to enhance empirical mode decomposition for power quality applications［C］// Proceedings of IEEE Power Engineering Society General Meeting，June 24 －28，2007，Tampa，FL，USA:Tampa，2007:1 －6.

［11］胡红英，殷福亮.频率外差经验模式分解改进算法［J］.农业机械学报，2010，41(10):209 －213.

［12］李成鑫，刘俊勇，姚良忠，等.基于改进频移经验模态分解的低频振荡参数提取［J］.电力系统自动化，2012，36(15):8 －13.