DEM坡向提取的向量场模板匹配方法

李润超，袁林旺，李 硕，朱晓林，俞肇元

南京师范大学 虚拟地理环境教育部重点实验室，江苏 南京 210023

1 引 言

坡向在数学上定义为地表面一点切平面的法线矢量在水平面的投影与过该点的正北方向的夹角，坡向表征了地面点高程改变量的最大变化方向。目前计算坡向的数学计算模型主要利用DEM 数据采用二阶或三 阶差分 的方法［1－2］，均属于直接基于标量场进行计算，受DEM精度误差传递特性、地形复杂度等影响，多数坡向算法对DEM 高程数据误差敏感，算法稳定性不强［3－5］。DEM精度场数据可以描绘空间相关性规律，并可通过趋势面拟合来揭示地形整体结构性的变化［6］。矢量场数据除包含表征地理现象影响强度大小的数值外，还同时包含了方向信息，因此，利用DEM数据构建矢量场来表征和计算坡向，更能真实地描述其本质特征，具有更好的整体结构性。

几何代数（克利福德代数）是基于四元数和格拉斯曼扩张代数等发展的具有多维统一和维度无关特性的代数系统，已在计算机视觉和人工智能等领域得到广泛应用。利用几何代数的旋转rotor算子，可以实现多维场数据局部特征的自适应模板匹配，进而可构建同时揭示数据整体和局部特征的自适应性通用模板，进而可构建求解场数据特征解析的算法［7－11］。本文通过构建正北方向的模板向量场和栅格高程梯度向量场，利用几何代数中旋转算子rotor来拟合两个向量场进行坡向求解。基于高斯曲面模拟数据对方法的正确性、窗口选择、误差分布进行了验证，最终基于实际DEM数据进行了案例验证与对比。

2 基于几何代数的坡向表达方法

2.1 梯度场和模板向量场的几何代数表达

在几何代数中，空间可以直接被定义为向量集合间的运算，空间维数直接由运算法则确定。给定几何代数空间Cln，空间格网场F中的任一向量a可定义为：a＝xae1＋yae2＋…＋waen，其中e1、e2、…、en为几何代数空间Cln的基向量，xa、ya、…、wa为a在各基 向量 上的 投影大小［12－13］。几何代数中几何积的结果为一个混合维度的向量，也叫做多重向量，多重向量是几何代数的基本数学结构，其定义为

式中，A＝｛n，s，…，t｝。可定义以多重向量为基本元素的多重向量场函数f（M）为

上式将不同维度向量间计算直接统一于几何积，实现了不同维度场的统一表达与计算。

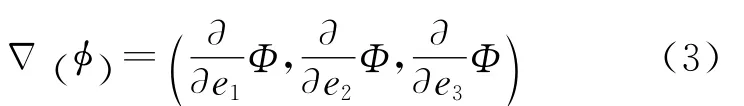
对于栅格DEM数据，可以将其视为简单的标量场数据（如图1）。通过DEM的高程值来构建几何代数中的多维向量（multivector），每个栅格点都对应一个multivector。坡向的高程变化梯度即高程变化率，可以分别求X方向和Y方向的高程变化梯度grad（x）（x，y）和grad（y）（x，y），利用文献［14］介绍的中心梯度求解模板，X方向和Y方向的梯度求解公式为

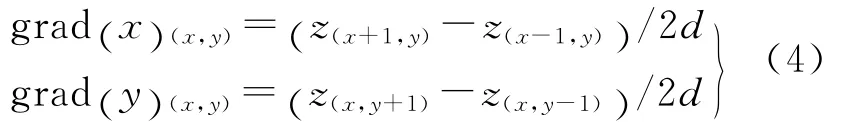
式中，z（x，y）表示点（x，y）处的高程；d表示格网精度；grad（x）（x，y）表示点（x，y）处X方向的梯度；grad（y）（x，y）表示点（x，y）处Y方向的梯度；grad（x，y）表示点（x，y）的梯度。对于多重向量场f（x），上式可写成如下形式

2.2 基于平行模板的坡向求解

对DEM的栅格点，可以通过构建以该点为中心和行列为奇数的窗口来表示目标梯度场。定义平行模板g（x，y）＝e1sinθ＋e2cosθ，其中角度θ用于限定模板朝向，图2所示为窗口大小为3，朝向正北方向（θ＝0°）的平行模板。根据rotor的定义，多重向量场f（x，y）可写成如下形式

式中，R表示由模板g（x，y）变换为f（x，y）的rotor；ε（x，y）为残差项，由rotor的定义可知，当选取g（x，y）指向正北方向时，R即表示由正北方向变换到f（x，y）的旋转，则坡向θ的求解可转化为对rotor的求解。

图1 高程标量场和正北方向模板Fig.1 The scalar field of elevation and the northern template

3 基于几何代数的坡向求解与提取

3.1 基于矩阵分解SVD方法的rotor反解

几何代数中的旋转算子rotor具有可合成性、保形性和自反性等特性，可实现任意几何体旋转变 换 的 多 维 统 一 表 达［15－16］。 给 定 任 意 multivector对象和rotorR，其旋转变换为

由于rotor的整体保形性，可将上述公式推广至向量场，给定向量场F＝ ｛a1，a2，…，an｝，其旋转变换为RFR－1＝ （Ra1R－1）＋ （Ra2R－1）＋…＋（RanR－1），R作用于向量ai的旋转包括两个要素：基平面和角度，基平面的对偶向量即ai绕过的旋转轴。将R写为指数形式，可显式求得其所内蕴的旋转轴和旋转角度

式中，I为旋转平面；φ为旋转角度；p、q为旋转平面上任意两个角度为φ的vector；I也可用两向量的外积p∧q来表示。

定义n维几何代数空间Cln，rotorR可用几何代数方程RAR－1＝B表示，也可记为RA＝BR。在该形式下等同于特征多重向量方程RA＝λR，λ为标量。如果存在一系列的多重向量JB：＝｛J∈Cln：JB＝BJ｝满足（JBR）A－B（JBR）＝0，则JB为rotor的解空间，且JB的维度是2n。在三维欧式空间中，rotor是一个标量和一个二维向量的和，定义两个单位向量a、b∈Cl3。需要求解R使其满足RaR－1＝b，由于rotor可以写作R＝eUabθ／2，Uab是bivector表示的单位平面的二重矢量，θ是旋转角度。通过求解式中Ra－bR＝0的R，可得结果集JR：＝｛Rab，bRab，UbRab，IRab｝，其中I是Cl3空间中的伪标量并且Ub＝bI－1，解集JR中最优解即为所求。

对标准向量场F′＝ ｛a1，a2，…，an｝和目标向量场F＝ ｛b1，b2，…，bn｝，可根据F＝RF′R－1来求解rotorR。构建向量场矩阵F，求解rotorR的最优解可以转化成对矩阵F的SVD分解，求得酉矩阵U、V，并通过公式R＝VUT求解最佳拟合rotor［11］。矩阵F的SVD分解为

3.2 基于几何代数解析坡向角度

在几何代数空间中，rotor算子不仅实现了任意对象的旋转变化，其表达中也包含了变换的角度与旋转平面等信息。据式（8）所示的rotor的指数形式表达，有如下关系

式中，θ和i2分别为rotor的旋转角度和旋转平面，再利用取维度算子〈〉n，旋转角度θ可通过下式求得

解析出角度θ的余弦值，反解三角函数cosθ／2得到θ的角度值，即为坡向角度。将求得角度按照8个方向对栅格坡向角度进行分类赋值（如表1），即可得各位置点坡向值。

表1 坡向值分类Tab.1 Classification of slope value

4 算法设计与试验验证

4.1 基于几何代数坡向提取算法流程

根据上述分析，基于几何代数坡向提取算法的基本步骤如图2。

图2 几何代数提取坡向算法流程Fig.2 The algorithm flow of slope extracting based on geometric algebra

（1）根据窗口大小n和公式（5），求解n×n窗口的每个栅格的梯度grad（x，y），构建梯度向量场Fi。

（2）构建同样窗口大小的正北方向的向量模板M，初始化相关参数。

（3）利用正北模板向量场M和梯度向量场Fi基于rotor拟合逼近，建立关系式，Fi＝RMR－1，基于SVD反解rotor，对该rotor解析，获取rotor的类型及特征参数，通过对角度值θi的分类，得到n×n窗口中心栅格点的坡向。

（4）移动窗口，迭代数据，反解并解析rotor，得到θ并存储在栅格中，直至所有数据都被处理得到全部栅格的坡向。

4.2 模拟试验与验证

传统的DEM坡向计算均是基于高程变化率的窗口卷积运算，其计算模型为

式中，fx、fy分别是东西和方南北方向的高程变化率。根据求解fx和fy的不同而演化成不同方法。现有算法中三阶差分算法有平滑和过滤作用，避免极端数据影响，误差相对较小，可靠性较高［17－18］，被 ArcGIS等行业软件普遍采用。本文选取了三阶反距离平方权差分法进行算法对比。

为考察算法的正确性，试验应用模拟高斯地形合成曲面，并离散为特定尺度的DEM曲面，高斯合成曲面参数方程的定义为

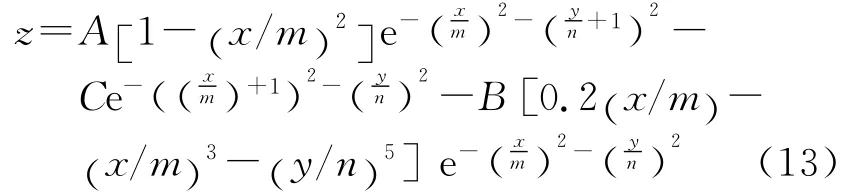
式中，A、B、C为地势起伏参数；m、n为范围控制参数。基于数学曲面建立的DEM数据由于消除了格网点数据误差，同时可根据Z的表达式直接求解出x和y方向上的偏导数fx和fy，结合公式（12）求得坡向真值，即可支撑算法对比与精度验证［19－20］。

取A＝3，B＝10，C＝1／3，m＝500，n＝500，标准差为1.314 6，均值为0.627 1，格网分辨率为10×10构建地形曲面（图3a）。在3×3、5×5、7×7窗口下，利用rotor算子拟合和基于ArcGIS的三阶反距离平方权差分进行坡向计算，两种算法三种窗口的计算结果与真值坡向均一致，表明算法计算结果的正确性。

为验证算法的稳定性，对模拟DEM数据分别添加0.02、0.04、0.06、0.08、0.1倍标准差的高斯噪声，对加噪声DEM数据同样在3×3、5×5、7×7窗口下应用两种方法分别计算坡向，与真值坡向的比较分析结果如图3（b）所示。结果表明，随噪声增加，三阶反距离平方权差分法的精度变低，表明当地形较破碎时，算法的稳定性降低，噪声干扰的影响加大，与真值坡向的一致性也变差。而几何代数算法受到的干扰相对要小，且窗口越大受到噪声的干扰越小。表明本文算法的抗噪性较反距离平方法要好。

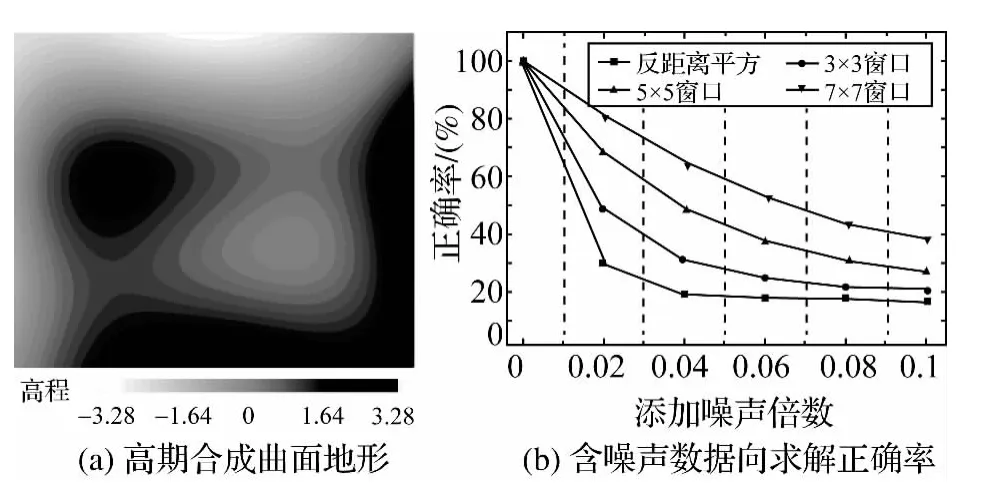
图3 高斯地形合成曲面和坡向求解结果对比Fig.3 The topography surface composited by Gaussian function and the compare of slope solving results

为验证方法的普适性、抗噪能力以及不同窗口大小下坡向精度的分布特征，对添加数据0.02倍标准差噪音的每组DEM数据，分别提取不同大小窗口中各曲面的山脊线和山谷线，坡向计算误差点的空间分布（图4）。对于不同的DEM数据，各种窗口的算法对地形复杂度不敏感，正确率大致相当。在误差点的空间分布上，误差点随着窗口增大而减少，并且总体构型和山脊线和山谷线吻合。这可能与山脊线和山谷线是两个不同坡向地形面的交线有关。总体上，窗口越大，正确率越高，保形性越好，但窗口过大容易导致边界数据缺失。基于不同窗口大小的多次模拟试验结果显示，当原始采样数据精度较高，需要细节的坡向分布时，3×3窗口即可获得较好的效果。当数据中存在明显噪音时，选取5×5或7×7窗口可获得很高精度。

图4 不同场景下错误点位的空间分布Fig.4 The distribution of slope error computed by different algorithms

4.3 DEM坡向求解案例验证

为验证算法在不同窗口下的稳定性和适用性，选取不同窗口的坡向求解模板，对黄土高原地区丘陵、梁、峁等典型地貌类型5m×5m分辨率的DEM数据进行统计和对比分析。选用方向统计量计算工具包CircStat［21］分别计算坡向数据的均值、标准差、峰度和偏度。计算结果如图5和表2所示。各地貌类型的坡向统计值均存在跃变过程（图中虚线），且不同统计量发生跃变的窗口大小大体一致。考虑到小窗口对地形保真度较好，而大窗口去噪能力较强，该跃变大致对应于坡向计算的最优窗口。黄土丘陵、梁、峁、塬和风沙地貌的最优窗口大小分别是13、11、11、11和17。

图5 真实地形数据坡向结果Fig.5 The slope results of real terrain data

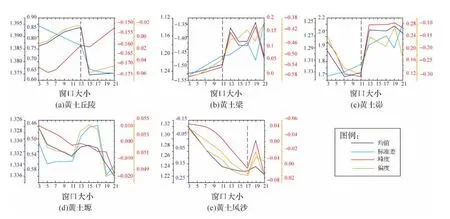
图6 不同窗口坡向统计量结果Fig.6 The statistical result of terrains slope with different window size

5 结 论

坡向作为向量的方向，常用算法多将其视为标量来计算，基于向量场拟合方法对求解实际地形坡向更具有现实意义。本文通过几何代数模板匹配方法构建了用于地形坡向计算的标准模板与地形变化率向量场模板，用rotor旋转算子进行向量场拟合，反解rotor进行角度解析获取地表坡向值。结果显示，该算法较反比例平方权算法有更好的整体性，且抗噪性好。基于5种典型地形的实例分析显示，黄土丘陵、梁、峁、塬和风沙地貌的最优窗口大小分别是13、11、11、11、17。黄土梁、黄土塬地貌一致性较强，所需计算窗口较小，而风沙和峁由于细节结构相对较多，选取更大的窗口更有助于获得稳定的结果。而黄土丘陵的窗口则介于上述两类之间。由于窗口越大，计算复杂度增加，计算效率趋于降低，建立面向大范围坡向计算的并行算法并进行经验参数率定是本文未来的研究方向。

［1］ AI Tinghua，LIU Yaolin，HUANG Yafeng.The Hierarchical Watershed Partitioning and Generalization of River Network ［J］.Acta Geodaetica et Cartographica Sinica，2007，36（2）：231－236，243.（艾廷华，刘耀林，黄亚锋.河网汇水区域的层次化剖分与地图综合［J］.测绘学报，2007，36（2）：231－236，243.）

［2］ CHEN Nan，WANG Qinmin，TANG Guoan.Comparative Analysis of the Algorithms of Aspect Deriving from DEM：Take the Study of Loess Hill and Gully Area as the Case［J］Remote Sensing Information，2007，（1）：70－75.（陈楠，王钦敏，汤国安.基于DEM的坡向提取算法对比分析：以黄土丘陵沟壑区的研究为例［J］.遥感信息，2007，（1）：70－75.）

［3］ LIU Xuejun，BIAN Lu，LU Huaxing，et al.The Accuracy Assessment on Slope Algorithms with DEM Error Spatial Autocorrelation［J］.Acta Geodaetica et Cartographica Sinica，2008，37（2）：200－206.（刘学军，卞璐，卢兴华，等.顾及DEM误差自相关的坡度计算模型精度分析［J］.测绘学报，2008，37（2）：200－206.）

［4］ LU Huanxing，LIU Xuejun，JIN Bei.Stochastic Process Based Accuracy Field Model for Grid DEM ［J］.Acta Geodaetica Et Cartographica Sinica，2012，41（2）：273－277.（卢华兴，刘学军，晋蓓.基于随机过程的格网DEM精度场模型［J］.测绘学报，2012，41（2）：273－277.）

［5］ LI Tianwen ，LIU Xuejun，TANG Guoan.Influence of Terrain Complexity on Slope and Aspect［J］.Journal of Mountain Research，2004，22（3）：272－277.（李天文，刘学军，汤国安.地形复杂度对坡度坡向的影响［J］.山地学报.2004，22（3）：272－277.）

［6］ BI Xiaoling，LI Xiaojuan，HU Zhuowei，et al.Analysis of the Influence of DEM Grid Size on the Accuracy of Topographical Factors［J］.Science of Surveying and Mapping，2012，37（6）：150－152.（毕晓玲，李小娟，胡卓玮，等.DEM网格尺寸对地形因子精度的影响分析［J］.测绘科学，2012，37（6）：150－152.）

［7］ ZHANG Juqing，LIU Pingzhi.Combining Fitting Based on Robust Trend Surface and Orthogonal Multiquadrics with Application in DEM Fitting［J］.Acta Geodaetica et Cartographica Sinica，2008，37（4）：526－530.（张菊清，刘平芝.抗差趋势面与正交多面函数结合拟合DEM数据［J］.测绘学报，2008，37（4）：526－530.）

［8］ GREEN A C，MARSHALL S，GREENHALGH D，et al.Design of Multi－mask Aperture Filters［J］.Signal Processing，2003，83（9）：1961－1971.

［9］ YANG J，LI S.Smoothness of Multivariate Refinable Functions with Infinitely Supported Masks［J］.Journal of Approximation Theory，2010，162（6）：1279－1293.

［10］ MA T，WANG S.Structural Classification and Stability of Divergence－free Vector Fields［J］.Physica D：Nonlinear Phenomena，2002，171（1－2）：107－126.

［11］ LUO Wen，YUAN Linwang，YU Zhaoyuan，et al.Adaptive Template Matching Method for Convergence and Divergence Characteristics of Multi－Dimensional Vector Fields［J］.Acta Electronica Sinica，2012，（9）：1739－1734.（罗文，袁林旺，俞肇元，等.多维向量场辐散辐合结构特征自适应匹配方法［J］.电子学报，2012，（9）：1739－1734.）

［12］ DORST L，FONTIJNE D，MANN S.Geometric Algebra for Computer Science［M］∥The Morgan Kaufmann Series in Computer Graphics.San Mateo：Morgan Kaufmann，2008.

［13］ PERWASS C，LASENBY J.A Unified Description of Multiple View Geometry［C］∥Proceedings of Geometric Computing with Clifford Algebra（G.Som－mer，ed.）.Berlin：Springer－Verlag，2001.

［14］ EBLING J，SCHEUERMANN G，CLIFFORD.Convolution and Pattern Matching on Vector Fields［C］∥ Proceedings of IEEE Visualization＇03，IEEE Computer Society.Los Alamitos：［s.n.］，2003：193－200.

［15］ DORAN C，LASENBY A.Geometric Algebra for Physicists［M］.Cambridge：Cambridge University Press，2003.

［16］ HESTENES D.New Foundations for Classical Mechanics［M］.New York：Kluwer，2002.

［17］ LI Tianwen，LIU Xuejun，CHENG Zhengjiang，et al.Study on the Accuracy and Algorithms for Calculating Slopes and Aspects Based on the Digital Elevation Model［J］.Arid Land Geography，2004，27（3）：398－403.（李天文，刘学军，陈正江，等.规则格网DEM坡度坡向算法的比较分析［J］.干旱区地理，2004，27（3）：398－403.）

［18］ LIU Xuejun，GONG Jianya，ZHOU Qiming，et al.A Study of Accuracy and Algorithms for Calculating Slope and Aspect Based on Grid Digital Elevation Model（DEM）［J］.Acta Geodaetica et Cartographic Sinica，2004，33（3）：258－263.（刘学军，龚健雅，周启鸣，等.基于DEM坡度坡向算法精度的分析研究［J］.测绘学报，2004，33（3）：258－263.）

［19］ TANG G.A Research on the Accuracy of Digital Elevation Models［M］.Beijing：Science Press，2000.

［20］ JIA Yini，TANG Guoan，LIU Xuejun，et al.The Impact of Elevation Interpolation on the Accuracy of Gradient and Aspect from DEMs［J］.Journal of Geo－Information Science，2009，11（1）：36－41.（贾旖旎，汤国安，刘学军.高程内插方法对DEM所提取坡度、坡向精度的影响［J］.地球信息科学学报，2009，11（1）：36－41.）

［21］ BERENS P.CircStat：A MATLAB Toolbox for Circular Statistics［J］.Journal of Statistical Software，2009，31（10）：1－21.