多尺度分形压缩感知遥感成像方法
刘佶鑫,孙权森
1.南京邮电大学 宽带无线通信技术教育部工程研究中心,江苏 南京 210003;2.南京理工大学 计算机科学与技术学院,江苏 南京 210094
1 引 言
随着软硬件技术的进步,对地遥感观测在测绘领域的作用越来越重要。而高分辨率和大视场角已成为遥感成像的一种主流发展趋势。以新近发射的光学遥感卫星(如美国的 WorldView-2、法国的Pleiades、以色列的EROS-C等)为例,其分辨率普遍优于1m且轨道高度普遍达到600km及以上。遥感成像的这一特点将为测绘应用的信息处理提供高精度的数据保障,同时也对中、高分辨率遥感的成像质量和处理效率提出了要求。
遥感成像的基础是数字信号处理技术,而以香农采样定理为基础的传统数字信号处理技术随着遥感成像的发展将面临海量数据处理的难题。香农采样定理指出:对于任意带限信号,采样频率必须达到信号带宽的两倍及以上。因此,传统数字信号处理的研究重点集中在两方面:其一,提高采样频率。对遥感成像而言意味着需要研制分辨率更高的大型面阵传感器,这将大幅提高遥感卫星的生产及发射等综合成本。为此,文献[1]对LMCCD提出了改进,而文献[2]则尝试消除大面阵CCD影像的多通道不一致性;其二,限制信号带宽(如低通滤波器)。这必将损失大量的细节信息,降低高分遥感的数据高精度优势。在滤波器研究领域,文献[3]基于学生化残差提出了模糊自适应滤波算法,而文献[4]则运用推扫成像滤波器模型来进行星载相机轨道末期成像及图像复原。可见,以香农采样定理为基础的传统信号处理方式从某种程度上制约了数字遥感成像的发展。
作为一种新型信号处理技术,压缩感知(compressive sensing,CS)为海量数据处理提供了不同于传统方式的新思路。CS理论是由文献[5—6]和文献[7]分别提出的。该理论认为,通过随机过完备观测矩阵的投影运算能够在保持全局信息的条件下合并完成信号的采样与压缩,而在此基础上求解一个欠定方程的l1范数最小化问题来完成信号重构。目前,CS理论在数字成像方面已得到初步应用,如单像素相机[8]、光谱成像[9]、MRI成像[10]等。此外,文献[11]阐述了 CS对解决数字洪灾的重要意义。但是,在CS遥感成像方面,除了文献[12—13]以小波阈值为基础的系列研究外,其他成果相对较少。
本文针对CS遥感中重构运算开销大和成像细节质量低的问题,提出一种以多尺度透镜组为基础的分形压缩感知遥感成像方法。多尺度透镜成像模式能够大幅降低基于稀疏字典的CS成像的运算开销,而以分形维度代替l1范数作为目标函数能够较好的改善弱约束条件下CS成像质量,并在较大限度上提高细节信息的复原效果。
2 压缩感知成像原理
CS成像分为采样和重构两部分。首先,假设原始信号x∈RN,其CS采样如下

式中,Φ为随机观测矩阵。式(1)是对信号x的降维投影(即压缩);而Φ列的集合具备过完备不相干性,保证了y包含原始信号x的几乎全部信息,因此称为感知。观测结果y即所谓的感知数据。
其次,重构的核心是欠定矩阵伪逆运算。如果x具有稀疏性(即x中有K个非零元素且K≤M)且Φ满足RIP(restricted isometry property)时,式(1)求逆可等价为
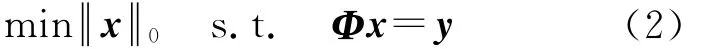
虽然式(2)在理论上有全局最优解,但是l0范数最小化是NP难题,且运算开销极高。文献[14]提出了基追踪(basis pursuit,BP)算法来解决这个问题,描述如下
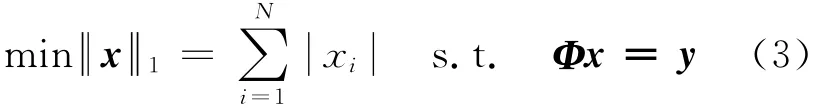
式(3)可以通过线性规划求解。而将BP用于CS重构是文献[5-7]完成的证明。CS理论认为:在一定条件下,式(3)中l1范数最小化的最优解等价于式(2)中l0范数最小化的全局最优解。这就为CS框架的应用提供了重要的理论支撑。
对二维图像,多数CS框架是将图像拉伸为一维向量进行处理。这种方式能够较好地满足CS运算的要求,且处理方式简便、运算开销相对较小,但是其重构质量往往不能令人满意。为此,文献[5]采用 TV(total variation)模型将CS重构算法改进为

式中,D为梯度算子。但是这种二维处理模式显然比一维的l1范数最小化方式复杂,不能较好地适用于对时效性要求较高的数字成像等应用。
但是在实际应用中,信号直接满足稀疏性的情况并不常见。实际上,大多数遥感数字图像在空域下都不具有稀疏性。而CS成立则必须满足两个重要条件:① 过完备观测矩阵必须具备RIP。② 待重构信号必须是稀疏的。为此,一种更为普遍的CS改进算法可以描述如下

式中,α即为x在基空间Ψ下的稀疏表示。文献[5-6]的研究指出,几乎所有的信号总能找到合适的基空间(如小波域、傅里叶域等)来实现稀疏表示。因此,稀疏字典的应用解决了遥感成像在CS框架下的有效性问题。
虽然稀疏表示的引入既保留了BP算法的简易性又解决了重构信号对稀疏性的要求,但是稀疏表示本身的运算开销却十分巨大。假设一个过完备不相干字典可由如下Gabor函数生成

3 多尺度分形压缩感知遥感成像框架设计
3.1 多尺度透镜组成像
在图1中,横坐标表示5种图像分块大小,纵坐标表示各级尺寸大小对应的CS程序运算开销。由于运算开销正比于稀疏字典的维度,因此其关系描述如下

式中,n2为图像分块大小;c为常数。由此可见,分块成像的这种思路能够适合于高分辨率和大视场角遥感成像的应用需求,同时可以大幅缓解CS成像算法在高维图像处理中的海量运算开销难题。但是,新的问题是能否找到符合分块成像模式的图像传感器。

图1 图像大小与基于稀疏字典的CS成像运算开销水平Fig.1 The relationship between different image size and its computation cost level based on sparse dictionary
文献[16]设计的多尺度透镜组(multi-scale lens)成像模型为本文的研究提供了重要参考。如图2所示,大尺度透镜成像的优势在于有较大的视场角,缺点是成像面阵的工艺成本将随分辨率的提高呈现指数级增长;而小尺度透镜成像的优势则是以较低的工艺成本保持高分辨的图像细节信息,缺点却是较小的成像面阵难以满足大视场角观测的需要。在此基础上,文献[16]尝试将不同尺度的透镜组合用于形成多尺度透镜,其试验结果(见图2)取得了较好的大视场角高分辨成像效果。因此,多尺度透镜组能够集合两种成像方式的优点,不仅满足本文对遥感CS成像的分块需求,而且其各子块成像面阵的研制成本和工艺难度也远低于传统上用于大视场角遥感成像的大尺度面阵。

图2 多尺度透镜组的成像原理Fig.2 The principle of multi-scale lens Imaging
3.2 分形压缩感知成像方法
多尺度透镜组的引入解决了CS遥感成像中大视场角的问题,但是作为测绘领域定量遥感的特殊需求,中、高分辨率遥感图像细节信息的质量直接决定了其应用效果,因此如何提高CS重构精度是关系到中、高分遥感成像的另一个关键问题。
在遥感成像领域,普遍认可的压缩比通常在4∶1左右。从图3中可见,压缩比在4∶1左右的CS重构质量十分不理想,而感知次数越高往往成像精度越佳。因此,在传统的CS成像应用中,低压缩比的成像质量并不能满足遥感的要求。这就与遥感应用的需求形成了矛盾。

图3 传统CS成像在不同感知次数下的图像重构Fig.3 Image recovery under different sensing time of traditional CS imaging
传统CS成像的实质是求解如式(3)或式(6)的l1范数最小化问题。对于高维信号CS重构而言,如果约束条件过于严格也将大幅增加运算开销。因此,普遍的处理思路是将式(6)弱化为如下关系

式中,ε为任意小的正数。尽管这一处理方式使得CS重构求解的可行性大为提高,但是由于作为目标函数的l1范数的自身特性,使得CS重构在信号细节复原上的质量不佳。
与l1范数相比,分形维度作为一种测度函数适用于欧几里得空间Rn中各种维度集合的测度。由于分形维度能够包含信号的几何结构信息,因此它可以作为一种分析复杂数据集的有效工具。在各类分形维度中,计盒维度(box counting dimension,BCD)非常适合计算机实现。BCD的定义为:假设F是Rn的任意非空有界子集,由覆盖F的最长直径δ的最小集合数量计为Nδ(F),则F的BCD的下界和上界分别表示为
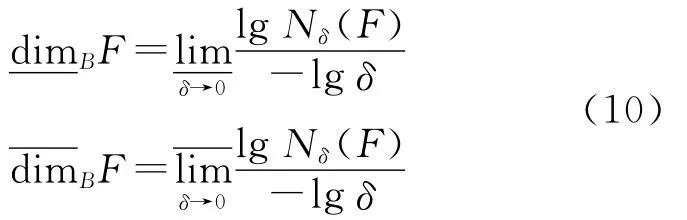
若二者相等,则称其为F的BCD,记为

假设两组离散信号的向量形式为V1=[30,50,-20,40,10]T和V2= [31,49,-20,38,11]T,分别按照l1范数和分形维度进行度量。图4中横坐标i为向量元素序号,纵坐标V(i)表示与之对应的元素值。图4显示,当信号存在细节差异时,l1范数不能有效地进行区分,而分形维度则明显的反映了二者的差异。因此,对于采用公式(9)的CS重构算法,以分形维度代替l1范数作为目标函数,本文将CS成像问题改进为

这里采用的目标函数是BCD的一种广延性更好的改进形式,即 Minkowski维度[17]。因此,将这种新的CS框架称为分形压缩感知(fractal compressed sensing,FCS)。在多尺度透镜组和分形压缩感知成像的基础上,笔者提出一套适合遥感成像的CS框架。
3.3 本文提出的遥感成像框架
图5是本文设计的多尺度分形压缩感知(multi-scale fractal compressed sensing,MFCS)遥感成像的系统框架,包括3个主要步骤:
(1)多尺度CS遥感采样。通过基于多尺度透镜组的卫星载荷平台传感阵列,实现大视场角的中、高分辨率遥感信号采样。
(2)感知数据稀疏字典选取。由模/数转换和信号传输,将感知数据传输到地面处理系统,选取合适当前感知数据的过完备冗余字典,用于后续的基于信号稀疏表示的成像重构运算。
(3)多尺度分形CS成像。以基于字典的稀疏表示为基础,通过迭代求解由式(12)和式(13)描述的分形最优化问题,最终计算完成中、高分辨率遥感CS成像。
至此,本文的MFCS遥感成像框架已经构建完成,下文将通过一系列试验及相关评价指标来讨论该成像方式的特性。

图4 l1范数与分形维度对信号细节差异的度量Fig.4 Measurement of l1-norm and fractal dimension to signals with details’difference
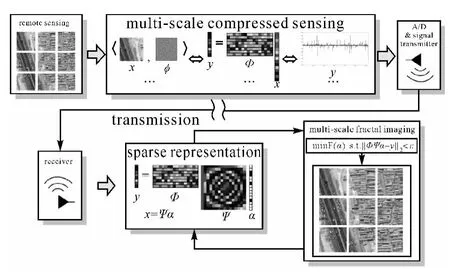
图5 多尺度分形压缩感知遥感成像框架Fig.5 Multi-scale fractal compressed sensing remote sensing imaging framework
4 试验及分析
试验选取3组卫星数据:① 由 WorldView-2提供的在2011年日本地震后拍摄的关于福岛第一核电站受损情况的0.5m级遥感图像[18]中的部分(图6(a)左边)。② 由SPOT 5拍摄的匈牙利某村庄在泥石流发生前的2.5m级遥感图像[19]中的部分(图6(a)中间)。③ 由 CBERS-2提供的北京市区的20m级遥感图像[20]中的部分(图6(a)右边)。由于试验是在普通PC(CPU是Intel Core Duo i5,内存4GB)上进行,当样本图像画幅过大,如果直接进行针对完整尺度下的CS重构,则会导致内存溢出等问题,因此所有遥感图像(完整尺度)的大小均采用200像素×200像素。这里主要研究BP和FCS两种方法分别在完整(200像素×200像素)和多尺度(100像素×100像素、50像素×50像素、25像素×25像素)情况下的成像效果。以100像素×100像素为例,当采用该尺度模式时,某一200像素×200像素的图像将分为4个100像素×100像素子区域进行处理。以此类推可知,对200像素×200像素的图像50像素×50像素的模式需要划分为16个子区域,25像素×25像素需要64个子区域。


图6 BP和FCS方法的成像效果Fig.6 The imaging result of BP and FCS
CS的信号压缩比采用4∶1。成像质量的评价指标包括3种:① 峰值信噪比(peak signal-tonoise ratio,PSNR)是一种基于像素级统计信息的客观评价标准,其数值越大说明成像结果在数值上越接近实际情况;② 结构相似性(structural similarity,SSIM)是模拟人眼视觉系统对几何结构的感知近似程度,其数值越接近1说明图像越有利于人工解译;③ 运算时间开销反映了各成像过程的求解时间开销情况,以s为单位。假设原始图像x为m×n,其CS成像结果为xCS,则PSNR按如下计算[21]

式中,μx是x的均值;μxCS是xCS的均值是x的方差是xCS的方差;是x和xCS的协方差;c1=(k1L)2和c2=(k2L)2中通常取L=28-1,k1=0.01,k2=0.03。
从图6可以看出,无论对中分辨率(20m)还是对高分辨率(2.5m和0.5m),FCS成像方式得到的图像在视觉效果上总体优于BP成像的效果;而MFCS成像方式又普遍强于完整尺度CS成像。图7则表明:① 从PSNR和SSIM可知,两种方式的指标数值基本随不同尺度图像大小的增加而呈现递减趋势,而MFCS方式的成像质量远高于BP方式。但无论是BP还是MFCS,若尺度划分太小则可能导致成像质量的略微下降(见25像素×25像素和50像素×50像素的对比)。② 尺度划分不大时,BP与MFCS的在运算时间开销上基本在持平。而多尺度CS成像方式与完整尺度CS成像相比,其运算开销将随尺度的降低大幅递减,这一点在中分辨率和高分辨率成像结果中都有所体现。总的来说,FCS方法符合遥感量化应用在中、高分辨率成像上对细节图像的质量要求,而MFCS成像方式则大幅降低了在稀疏表示基础上的运算开销,符合大视场角遥感成像的时效性需求,因此,本文提出的MFCS框架使得CS成像方式能够满足遥感成像及应用的需要。
5 结 论
本文在压缩感知成像理论的基础上,研究了其在遥感成像领域的应用方法。通过引入多尺度透镜组解决了基于稀疏表示的CS成像方式在大视场角观测条件下面临的运算开销大和时效性差等问题。并提出基于分形维度的CS成像方法用于改进中、高分辨率遥感成像在细节等级上的成像质量。在此基础上,构建了一种新的MFCS遥感成像框架。相关试验表明,MFCS方法无论在成像质量还是运算开销上都优于传统的以BP为代表的CS成像模式,能够适用于遥感在中、高分辨率和大视场角条件下的成像要求(图7)。

图7 BP和MFCS成像的3种评价指标对比Fig.7 Three indices of evaluation between BP and MFCS imaging
根据本文方法的适用条件,在今后的工作中有必要重点开展以下两方面研究:① 由于引入了多尺度透镜组的概念,因此需要研究在实际应用中如何平衡透镜组的尺度设置与成像平台的研制成本;②考虑到稀疏表示对CS成像的重要影响,因此需要进一步研究适用于遥感应用的稀疏字典设计。
[1] WANG Renxiang,HU Xin,YANG Junfeng,et al.Proposal to Use LMCCD Camera for Satellite Photogrammetry[J].Acta Geodaetica et Cartographica Sinica,2004,33 (2):116-120.(王任享,胡莘,杨俊峰,等.卫星摄影测量LMCCD相 机 的 建 议 [J].测 绘 学 报,2004,33 (2):116-120.)
[2] TONG Xiaochong,WU Yundong,WANG Hui,et al.The Eliminate Inconsistent Algorithm of Large Plane Array CCD Multiple Channel Images [J].Acta Geodaetica et Cartographica Sinica,2006,35(3):234-239.(童晓冲,吴云东,王慧,等.大面阵CCD影像多通道不一致性消除算法[J].测绘学报,2006,35(3):234-239.)
[3] LI Qingkui,LV Zhiping.Fuzzy Adaptive Kalman Filtering Algorithm Based on the Statistic oftDistribution[J].Acta Geodaetica et Cartographica Sinica,2008,37 (4):428-432.(李庆奎,吕志平.基于学生化残差的模糊自适应滤波算法[J].测绘学报,2008,37(4):428-432.)
[4] HE Xiaojun,JIN Guang,YANG Xiubin,et al.Imaging Model and Image Recovering Algorithms of Spaceborne Camera in the End of Orbit Life[J].Acta Geodaetica et Cartographica Sinica,2010,39(6):579-584.(贺小军,金光,杨秀彬,等.星载相机轨道末期成像模型及图像复原算法[J].测绘学报,2010,39(6):579-584.)
[5] CANDÈS E,ROMBERG J,TAO T.Robust Uncertainty Principles:Exact Signal Reconstruction from Highly Incomplete Frequency Information[J].IEEE Transactions on Information Theory,2006,52(2):489-509.
[6] CANDÉS E,ROMBERG J,TAO T.Near Optimal Signal Recovery from Random Projections:Universal Encoding Strategies?[J].IEEE Transactions on Information Theory,2006,52(12):5406-5425.
[7] DONOHO D L.Compressed Sensing[J].IEEE Transactions on Information Theory,2006,52(4):1289-1306.
[8] TAKHAR D,LASKA J N,WAKIN M B,et al.A New Compressive Imaging Camera Architecture Using Opticaldomain Compression[C]∥ Proceedings of Computational Imaging IV at SPIE Electronic Imaging.San Jose:[s.n.],2006.
[9] GEHM M E,JOHN R,BRADY D J,et al.Single-shot Compressive Spectral Imaging with a Dual-disperser Architecture[J].Optics Express,2007,15(21):14013-14027.
[10] LUSTIG M,DONOHO D L,PAULY J M.Sparse MRI:The Application of Compressed Sensing for Rapid MR Imaging[J].Magnetic Resonance in Medicine,2007,58(6):1182-1195.
[11] BARANIUK R.More Is Less:Signal Processing and the Data Deluge[J].Science,2011,331(6018):717-719.
[12] MA J,LE D F.Deblurring from Highly Incomplete Measurements for Remote Sensing[J].IEEE Transactions on Geoscience and Remote Sensing,2009,47(3):792-802.
[13] MA J.Single-pixel Remote Sensing[J].IEEE Geoscience and Remote Sensing Letters,2009,6(2):199-203.
[14] CHEN S S,DONOHO D L,SAUNDERS M A.Atomic Decomposition by Basis Pursuit [J].SIAM Journal on Scientific Computing,1998,20(1):33-61.
[15] ARTHUR P L,PHILIPOS C L.Voiced/unvoiced Speech Discrimination in Noise Using Gabor Atomic Decomposition[C]∥IEEE International Conference on Acoustics,Speech and Signal Processing.Texas:[s.n.],2003:820-828.
[16] BRADY D J,HAGEN N.Multiscale Lens Design[J].Optics Express,2009,17(13):10659-10674.
[17] TANG Y Y,TAO Y,LAM E C M.New Method for Feature Extraction Based on Fractal Behavior[J].Pattern Recognition,2002,35:1071-1081.
[18] WorldView-2Satellite Images.Japan’s Troubled Fukushima I Nuclear Power Plant[EB/OL].[2011-03-04].http:∥www.satimaging--corp.com/galleryworldview-2.html.
[19] SPOT-5Satellite Images.Toxic Red Sludge Village of Kolontar,Ajka,Hungary[EB/OL].[2011-01-05].http:∥www.satimag--ingcorp.com/gallery-spot5-images.html.
[20] CBERS-2Satellite Sensor Images.CBERS-2Satellite Image of Beijing[EB/OL].[2010-12-15].http:∥www.satimagingcorp.co- -m/gallery-cbers-2.html.
[21] HUYNH T Q,GHANBARI M.Scope of Validity of PSNR in Image-video Quality Assessment [J].Electronics Letters,2008,44(13):800-801.
[22] WANG Z,BOVIK A C,SHEIKH H R,et al.Image Quality Assessment:from Error Visibility to Structural Similarity[J].IEEE Transactions on Image Processing,2004,13(4):600-612.

