评五年命题 谈教学启示——江苏近五年高考解析几何命题的分析与启示

☉江苏省常熟市教育局教学研究室 江苏省常熟市殷伟康特级教师工作室 陈志江

江苏省从2005年全面实施高中新课程，2008年进行第一次新课程下的高考至今已五次．新课程下无论是教学方法还是教学内容，和以往相比都有较大的变化，尤其是平面解析几何部分．由于该部分有关知识一直是高考的重点和热点，对学生来说这部分内容一直是难点，对老师来说又往往感到这部分内容的教学效果总不如人意，教学中存在很多疑惑点，因此本文想通过对江苏近五年高考解析几何命题的分析来谈一些对这块内容的教学思考，以供大家参考，希望能让大家对这部分内容的高考复习有所收获．

一、试题概况

下表是江苏近五年高考解析几何命题的简要情况，包括题号、题型、考查知识及能力、分值．

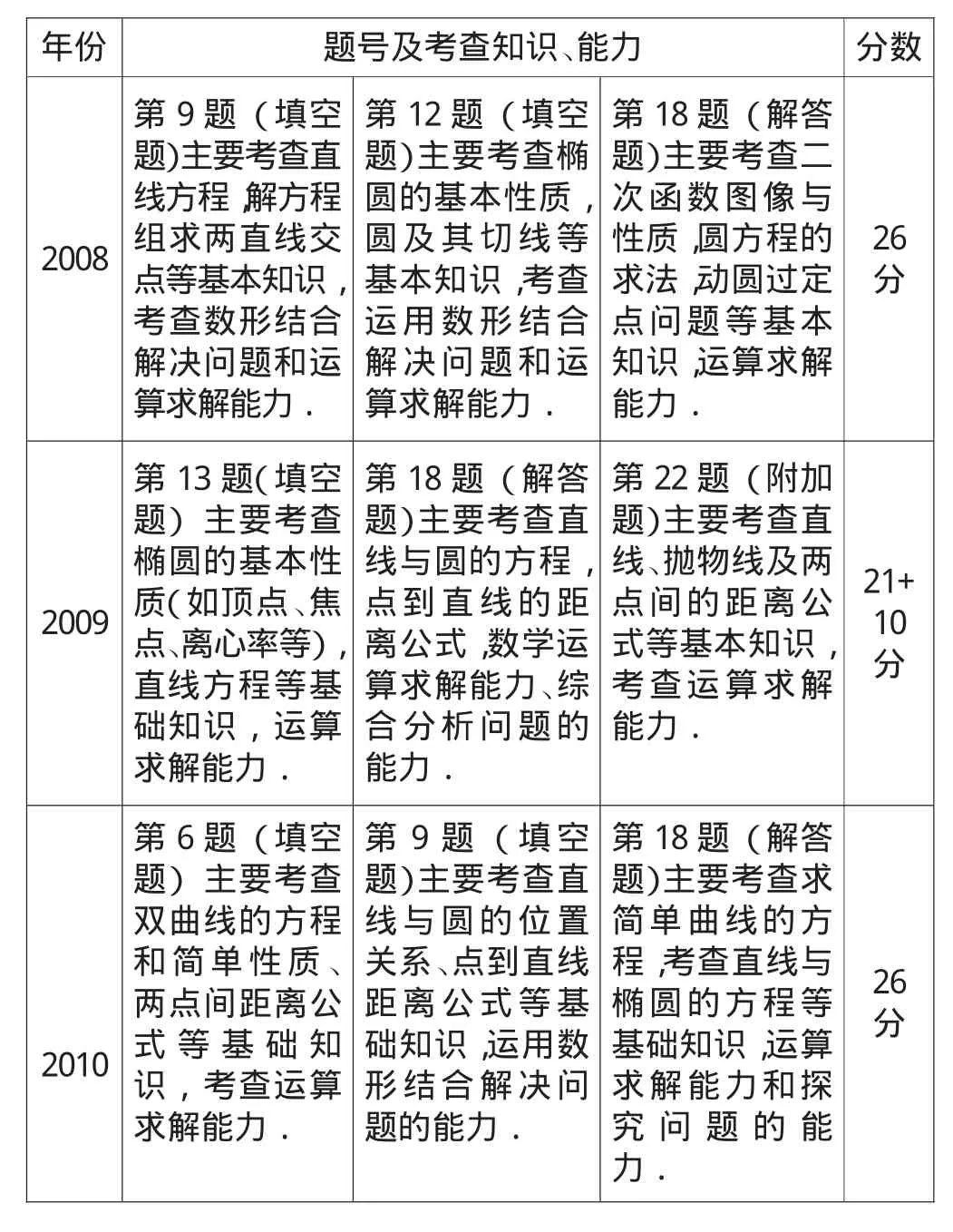
年份 题号及考查知识、能力 分数2008第9题（填空题）主要考查直线方程，解方程组求两直线交点等基本知识，考查数形结合解决问题和运算求解能力．第12题（填空题）主要考查椭圆的基本性质，圆及其切线等基本知识，考查运用数形结合解决问题和运算求解能力．第18题（解答题）主要考查二次函数图像与性质，圆方程的求法，动圆过定点问题等基本知识，运算求解能力．26分2009第13题（填空题）主要考查椭圆的基本性质（如顶点、焦点、离心率等），直线方程等基础知识，运算求解能力．第18题（解答题）主要考查直线与圆的方程，点到直线的距离公式，数学运算求解能力、综合分析问题的能力．第22题（附加题）主要考查直线、抛物线及两点间的距离公式等基本知识，考查运算求解能力．21+10分26分2010第6题（填空题）主要考查双曲线的方程和简单性质、两点间距离公式等基础知识，考查运算求解能力．第9题（填空题）主要考查直线与圆的位置关系、点到直线距离公式等基础知识，运用数形结合解决问题的能力．第18题（解答题）主要考查求简单曲线的方程，考查直线与椭圆的方程等基础知识，运算求解能力和探究问题的能力．

2011第14题（填空题）主要考查集合的表示与运算、圆环、二元一次不等式（组）表示平面区域等基础知识，灵活运用数形结合、等价转化的思想方法分析解决问题的综合能力．第18题（解答题）主要考查椭圆的标准方程及几何性质、直线方程、直线的垂直关系、点到直线的距离等基础知识，运算求解能力和推理论证能力．21分2012第8题（填空题）主要考查双曲线的方程及离心率等基础知识，考查运算求解能力．第12题（填空题）主要考查直线与圆的位置关系、点到直线距离公式等基础知识，运用数形结合解决问题的能力．第19题（解答题）主要考查椭圆方程的求解，直线与椭圆位置关系，两点间距离公式等基本知识，运算求解能力和运用数形结合、等价转化的思想方法分析解决问题的综合能力．26分

二、试题分析

1.试题命制遵循《考试说明》，突出重点内容的考查

从上表各题考查的知识来看，大部分题目是围绕直线、圆、椭圆来命制的，就解答题来说，2008、2009两年考查的是圆为载体的问题，2010、2011、2012三年考查的是椭圆为载体的问题．对照江苏高考《考试说明》解析几何部分所示的2个C级考点、6个B级考点和3个A级考点，我们可以看出五年的试题命制是完全遵循《考试说明》的．对要求理解和掌握的内容作为重点考查的内容（如圆与椭圆），每年都考，且有一定的难度，可能以难题形式出现（例如2011年14题、2012年19题）；对要求了解的内容也要考查，不过考查次数少，难度较小，往往以容易题形式出现（例如2010年第6题、2012年第8题）．

2.试题命制体现解析几何的本质，突出了对学生能力的考查

解析几何的本质是用代数方法去解决几何问题，即通过建立坐标系将几何问题归结为代数问题，然后通过对代数问题的研究去得到几何结果．从表中可以看出，五年的试题很好地体现了这一点，例如2009年的第18题就淋漓尽致地体现了用代数的方法解决几何问题的本质．

《数学课程标准》指出：高中数学课程应注重提高学生的数学思维能力，这是数学教育的基本目标之一．其中直观感知、观察发现、归纳类比、空间想象、抽象概括、符号辨识、运算求解、数据处理、演绎证明、反思与建构等思维过程，是数学思维能力的具体体现．不言而喻，从表中可以看出这些题目承载着对学生的运算求解、归纳类比、演绎证明等能力的考查．

3.试题的区分作用很好，对学生的考试成败影响很大

从表中分数栏看，2009、2011两年为21分，其余三年为26分，五年平均为24分，占试卷总分约为15%．解析几何题目的难度总体应属中上等，特别简单的很少，从考试来看这些题目无疑有很好的区分度．以2010年为例，三个题目的全省平均得分和难度系数如下表：

题号 第6题 第9题 第18题平均得分 4.06 2.25 6.67难度系数 0.81 0.45 0.42

应该说学生是否能做好这些题目，尽量多的拿到这15%的分数对他们的考试成败起着至关重要的作用．

三、教学启示

1.解析几何教学要遵循《教学要求》

江苏普通高中《课程标准教学要求》指出：理解直线的斜率和倾斜角的概念，理解直线的斜率和倾斜角之间的关系，掌握直线方程的几种形式的特点与适用范围……；掌握圆的标准方程与一般方程，能根据问题的条件选择恰当的形式求圆的方程……；掌握椭圆的定义和几何图形，掌握椭圆的标准方程，会求椭圆的标准方程；掌握椭圆的简单几何性质……

结合《考试说明》和五年的高考题可以看出，三者是非常吻合的，直线与圆是教学也是考查的重点内容，圆锥曲线部分椭圆是教学和考查的重点，双曲线和抛物线要求较低．所以在教学中，我们一定要明确这些内容，要按《教学要求》进行教学，要把新课程的理念真正落实到位．

2.新课程下不能穿新鞋走老路，要让学生真正减负

新课程下我们不能穿着新鞋走老路，要深入研究，给学生真正减负．例如随着韦达定理的淡出，很多利用韦达定理求解的直线与圆锥曲线问题也应随之退出舞台，再加上双曲线和抛物线教学要求的降低，那些不用韦达定理解决的直线与椭圆问题就是我们需要重点研究的问题了，因此这其实减轻了学生的学习负担，所以教学中老师要把握好方向．再如轨迹问题，由于“曲线与方程”内容仅是理科学生的选学内容，所以在文理科学生同卷的数学Ⅰ试卷部分出现考查轨迹问题可能性不大，而作为理科考生考的数学Ⅱ试卷附加题部分出现轨迹问题还是很有可能的，不过由于对该内容的教学要求是：“了解求曲线方程的一般步骤，能求一些简单曲线的方程”，所以即使考，难度应该也不会太大．因此我们老师在教学中要合理选择有关题目，大胆舍弃那些难度很大的轨迹问题，让我们的学生少做甚至不做无用功．

3.教学中要重点培养学生的数形转化能力和运算能力

解析几何题的解题过程大致可以归结为：几何条件——代数式子——运算求解——得出结论——还原几何结论．在这个过程中，几何不应该是考查的重点，它只是这个过程的开头和结尾，重点应该是如何将几何条件转化为代数式子和对代数式子进行运算求解，这当然也是难点．

（1）注重数形结合培养学生的转化能力

“数”和“形”是数学中的两个基本概念，它们是对立又统一的．数学大师华罗庚说过：“数无形少直观，形无数难入微．”而解析几何题是考查数形结合思想方法的最好载体之一．

教学中我们首先要让学生储备好平面几何的一些基本知识．例如与三角形相关的有三角形的三线，三角形面积的求法，三角形四心（外心、内心、重心、垂心）的性质；与圆相关的垂径定理，切线长定理，圆的切线与弦，圆心角与圆周角等；与曲线位置关系相关的有两直线的垂直与平行，直线与圆（椭圆）的相交、相切、相离，圆与圆的相交、相切、相离等．其次，要在数与形的相互转化这点上进行专项训练．例如2010年的第18题第三小问“设t=9，求证：直线MN必过x轴上的一定点（其坐标与m无关）”和2011年的第18题第三小问“对任意k>0，求证：PA⊥PB”，都要求先确定一个可以得到几何结论的数学式子，然后再看由条件如何来求得这个数学式子．由此看出，能否将几何条件（结论）与代数式子进行正确的相互转化是解决解析几何题的一大关键点．因此我们老师在平时的教学中要有意识地让学生体会转化过程，培养学生的转化意识，最终提高学生的转化能力．

（2）注重代数方法培养学生的运算能力

有效的转化是解题的前提，但是能否解出题目，还在于学生的运算求解能力．从近五年高考解答题的具体求解来看，并没有可用几何法直接简单获证的题目，所以教学中我们要注重代数方法培养学生的运算能力，这是解答解析几何题的另一大关键．笔者认为教学中要注意以下三点：第一要注意方程思想的应用．解析几何题目往往条件较多，需要引入多个变量，得到多个方程，因此用方程（组）解决解析几何题是不变的主题．由于涉及多个变量，所以学生往往感觉难以下手，教学中教师要重点分析如何处理方程（组），消元、整体代换、确定变量的主次转化为恒成立问题等都是常用的处理方法，教学中应结合题目让学生切身体会这些方法的应用；第二要注意培养学生耐心细致的运算习惯．由于韦达定理已不作要求，所以江苏省高考解析几何题的解题过程发生了变化，从“设而不求”转变成“设而求之”，这样就对学生的运算能力提出了更高的要求．例如2012年第19题第二问，解题思路很清楚，目标很明确，就是解出直线和椭圆的交点坐标，再利用两点间距离公式求出线段长度，但运算量较大，学生往往难以一算到底．第三，要注意解题后的反思和总结．孔子曰：“学而不思则罔．”我们的功夫不能仅仅花在解题上，更要用在反思和总结上，只有这样，我们才能实现新旧知识的同化和迁移，建构知识网络，深化对知识的理解，才能积累解题经验，优化解题方法，防止错误再犯，提高解题能力．

1.中华人民共和国教育部制订．普通高中数学课程标准（实验）［S］．北京：人民教育出版社，2003.

2.江苏省教育考试院．2012年普通高等学校招生全国统一考试（江苏卷）说明［M］．南京：江苏教育出版社，2011.

3.江苏省中小学教学研究室．普通高中课程标准教学要求［M］．南京：江苏教育出版社，2006.