纵观“立几”试题 感悟高考命题

☉江苏省丹阳市吕叔湘中学 李姣娟

综观全国各地的新课程高考数学试卷，不难发现对立体几何内容的考查，突出了对点、线、面之间的位置关系、角与距离的求解方法等立体几何主干内容的考查．试题设计比较灵活，以教材为基础、考能力为主．下面举例说明，供复习参考.

一、目标明确，循序渐进，倡导通性通法

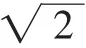
（1）证明：A′O⊥平面BCDE；

（2）求二面角A′-CD-B的平面角的余弦值.

图1

图2

同理可证A′O⊥OE.又OD∩OE=O，所以A′O⊥平面BCDE.

（2）几何法：如图3，过O作OH⊥CD交CD的延长线于H，连接A′H.

因为A′O⊥平面BCDE，所以A′H⊥CD，所以∠A′HO为二面角A′-CD-B的平面角.

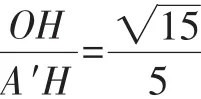
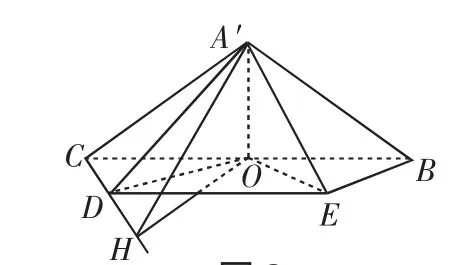
图3

图4

设n=（x，y，z）为平面A′CD的法向量，则

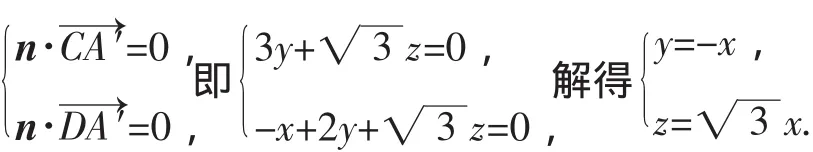
评析：常规方法往往需要构造空间辅助线、面，经过严密的逻辑推理进行论证和计算，而通过建立空间坐标系运用向量，则可以把“定性”问题转化为“定量”问题来研究，从而降低了解题思维量.

二、立足教材，注重双基，突显命题理念

例2（2011年北京文）如图5，在四面体PABC中，PC⊥AB，PA⊥BC，点D，E，F，G分别是棱AP，AC，BC，PB的中点.

（1）求证：DE∥平面BCP；

（2）求证：四边形DEFG为矩形；

（3）是否存在点Q，到四面体PABC六条棱的中点的距离相等？说明理由.

证明：（1）因为D，E分别为AP，AC的中点，所以DE∥PC.又因为DE⊄平面BCP，所以DE∥平面BCP.

图5

（2）因为D，E，F，G分别为AP，AC，BC，PB的中点，所以DE∥PC∥FG，DG∥AB∥EF.所以四边形DEFG为平行四边形.又因为PC⊥AB，所以DE⊥DG，所以四边形DEFG为矩形.

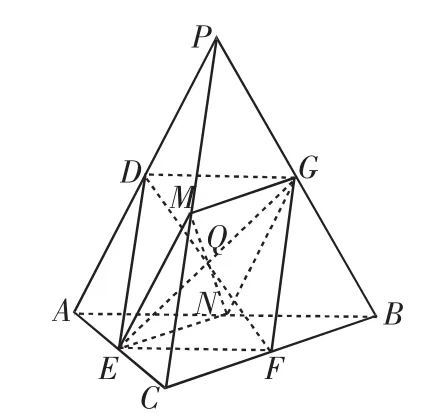
图6

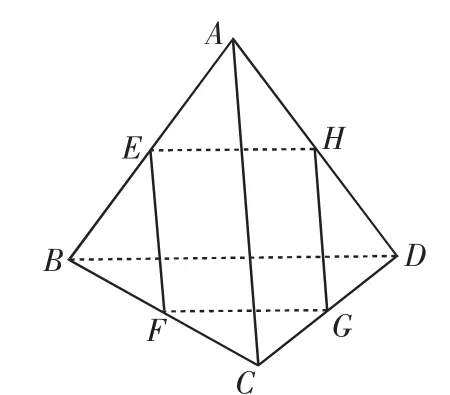
图7

课本探源：本题源自人教B版必修2第41页练习2：

如图7，已知在四面体ABCD中，AC=BD，而且E，F，G，H分别为棱AB，BC，CD，AD的中点，求证：四边形EFGH为菱形.

三、知识关联，纵横交汇，注重综合运用

例3（2013年福建理）如图8，在四棱柱ABCD-A1B1C1D1中，侧棱AA1⊥底面ABCD，AB∥DC，AA1=1，AB=3k，AD=4k，BC=5k，DC=6k（k＞0）.

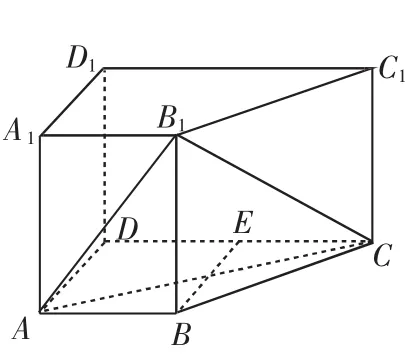
图8

（1）求证：CD⊥平面ADD1A1.

（3）现将与四棱柱ABCD-A1B1C1D1形状和大小完全相同的两个四棱柱拼接成一个新的棱柱，规定：若拼接成的新的四棱柱形状和大小完全相同，则视为同一种拼接方案.问：共有几种不同的方案？在这些拼接成的新四棱柱中，记其中最小的表面积为f（k），写出f（k）的表达式（直接写出答案，不必说明理由）.

解：（1）取CD的中点E，连接BE.

因为AB∥DE，AB=DE=3k，所以四边形ABED为平行四边形，所以BE∥AD且BE=AD=4k.

在△BCE中，因为BE=4k，CE=3k，BC=5k，所以BE2+CE2=BC2，所以∠BEC=90°，即BE⊥CD.又因为BE∥AD，所以CD⊥AD.

因为AA1⊥平面ABCD，CD⊂平面ABCD，所以AA1⊥CD.又AA1∩AD=A，所以CD⊥平面ADD1A1.

图9

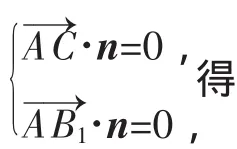
（3）共有4种不同的方案（略）.

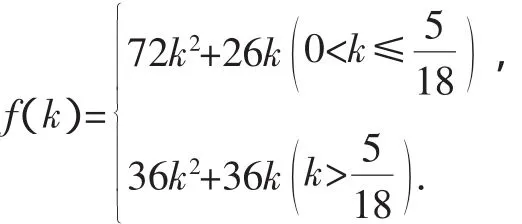
评析：本题主要考查直线与直线、直线与平面的位置关系、柱体的概念及表面积等基础知识，考查空间想象能力、推理论证能力、运算求解能力，考查数形结合思想、分类与整合思想、化归与转化思想、函数与方程思想的交汇综合运用．

四、问题开放，多向发散，考查应变能力

例4 （2013年安徽理）如图10，正方体ABCD-A1B1C1D1的棱长为1，P为BC的中点，Q为线段CC1上的动点，过点A，P，Q的平面截该正方体所得的截面记为S，则下列命题正确的是______（写出所有正确命题的编号）.

图10

解析：如图11，设截面S分别与CD、DD1、CC1、C1D1交 于M、N、Q、R.因为P为BD中点，所以CM=AB=DC，即M为定点，N为射线上的DD1动点，且DN=2CQ，AN=2PQ.通过确定N点再作出截面S与A1D1、C1D1的交点E、R，得答案①②③⑤.

图11