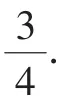拨开迷雾，探求隐藏在深闺中的线性规划问题

☉江苏省扬州市邗江区教育局 许兴震

☉江苏省扬州市邗江区公道中学 何长林 刘 勤

近年来，线性规划的命题方式发生了悄然改变，从以前的单一处理与线性规划有关的截距问题、斜率问题、距离问题等基础题型，向更高层次的中、高档题转变，并且在中、高档题中有关线性规划的特性并没有明显表现出来，这使得线性规划隐藏于深闺之中.笔者认为这种情况的出现恰恰是因为命题者将题目的背景进行了改变.因此探求隐藏在表面背景下的线性规划问题，关键是撇开题目的表面背景，探求题目中具有线性规划本质特征进行处理.由于此类题目比较多，笔者希望通过本文的几道例题，起到一个抛砖引玉的作用.

一、撇开函数、导数的背景，探求具有线性规划的本质特征

解析：因为f′（x）=x2+ax+2b，由题意可知：

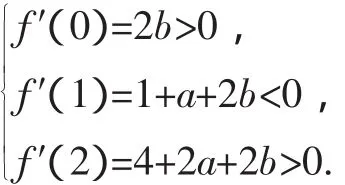
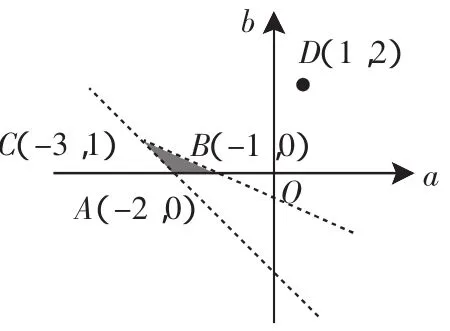
图1

二、撇开圆、向量的背景，探求具有线性规划的本质特征

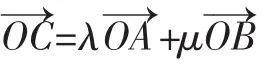
此时线性规划的特征就显露出来，只需以①为线性约束条件，利用线性规划中的有关距离问题处理方法处理即可.

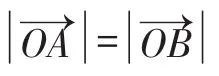
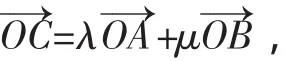
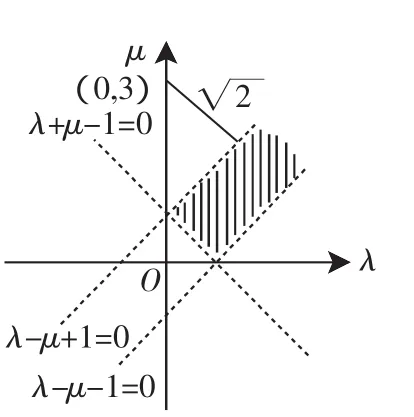
图2

三、撇开不等式的背景，探求具有线性规划的本质特征

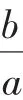
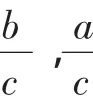
本题是以不等式为背景的线性规划问题.

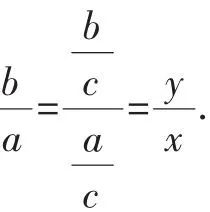
画出可行域.（如图3）

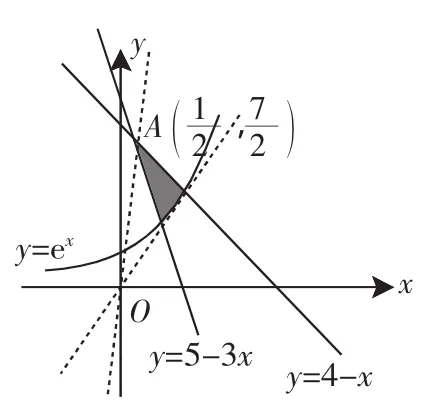
图3

当y=kx与y=ex相切是k取最小值.

设y=kx与y=ex相切于点（x0，y0），

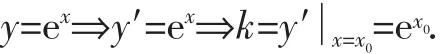
四、撇开数列的背景，探求具有线性规划的本质特征

例4 等差数列{an}中，已知a2≤7，a6≥9，则a10的取值范围是______.

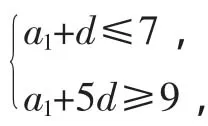
目标函数a10=a1+9d.

作出可行域（如图4），

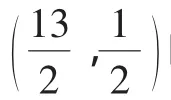
图4

五、撇开“斜率公式”的背景，探求具有线性规划的本质特征

例5 已知点A（2，3），B（-3，-2）.若直线l过点P（1，1）且与线段AB相交，则直线l的斜率k的取值范围是______.

分析：本题若通过数形结合，利用斜率公式求出kAP，kBP，再由k=tanα的图像得到直线l的斜率k的取值范围，不仅烦琐，而且容易出错.如果撇开求斜率，由直线l过点P（1，1）且与线段AB相交，直接得到A（2，3），B（-3，-2）在直线l的两侧（或在直线l上），那么本题利用线性规划知识就可以处理，而且比较容易.

解析：由题意，设直线l的方程为y-1=k（x-1），即kxy+1-k=0.