2012年高考湖南卷文科第16题的完整解答

☉北京市丰台二中 甘志国（特级教师）

高考题1（2012年湖南文16）对于n∈N*，将n表示为n=ak×2k+ak-1×2k-1+…+a1×21+a0×20，当i=k时，ai=1，当0≤i≤k-1时，ai为0或1.定义bn如下：在n的上述表示中，当a0，a1，a2，…，ak中等于 1 的个数为奇数时，bn=1；否则bn=0.

（1）b2+b4+b6+b8=______；

（2）记cm为数列{bn}中第m个为0的项与第m+1个为0的项之间的项数，则cm的最大值是______（.参考答案：3，2.）

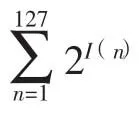
这两道高考题都是以二进制为背景且难度特别大，文献［1］对后者已作了深入研究，下面再对前者作研究.

笔者见到的正式出版的高考卷（比如［2］）及网络对高考题1第（2）问的解答均是错误的：

（2）设{bn}中第m个为0的项为bi，即bi=0，构造二进制数（i）10=（akak-1…a1a0）2，则akak-1…a1a0中 1 的个数为偶数.

①当a2a1a0=000 时，bi+1=1，bi+2=1，bi+3=0，cm=2；

②当a2a1a0=001 时，bi+1=1，bi+2=0，cm=1；

③当a2a1a0=010 时，bi+1=1，bi+2=0，cm=1；

④当a2a1a0=011 时，bi+1=1，bi+2=0，cm=1；

⑤当a2a1a0=100 时，bi+1=1，bi+2=1，bi+3=0，cm=2；

⑥当a2a1a0=101 时，bi+1=0，cm=0

⑦当a2a1a0=110 时，bi+1=1，bi+2=1，bi+3=0，cm=2；

⑧当a2a1a0=111 时，bi+1=1，bi+2=0，cm=1.

所以cm的最大值是2.

在该解答中，①-⑥的推理均是正确的，但⑦⑧的推理均是错误的：

⑦的反例——选a5a4a3a2a1a0=101110，得bi+1=1，bi+2=0，cm=1.

⑧的反例——选a4a3a2a1a0=10111，得bi+1=0，cm=0.

本文将给出这道题及其伴随问题的严谨解答.

定义1设正整数a是二进制数，记：

定义2设m∈N*，记：

（1）c（m）表示数列{A（n）}中第m个为 0 的项与第m+1个为0的项之间的项数；

（2）d（m）表示数列{A（n）}中第m个为 1 的项与第m+1个为1的项之间的项数；

（3）e（m）表示数列{A（n）}中第m个为 1 的项开始连续为1的项的项数；

（4）（fm）表示数列{A（n）}中第m个为0的项开始连续为0的项的项数.

先研究c（m）.

记数列{A（n）}中第m个为0的项对应的二进制数是a（得A（a）=0）.

当a的末位是1时，设a的末尾连续的1恰有k（k∈N*）个.

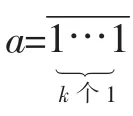
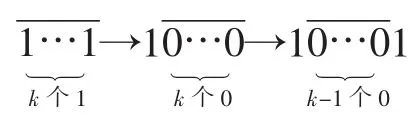
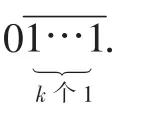
①当k为奇数时，得：

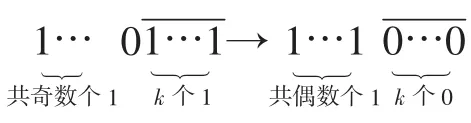
0→0，

c（m）=0.

②当k为偶数时，得：

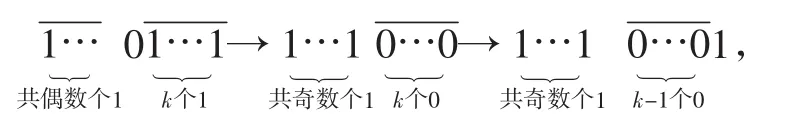
0→1→0，

c（m）=1.

当a的末位是0时，设a的末尾连续的0恰有k（k∈N*）个.

（1）当k≥2时，得：

0→1→1→0，

c（m）=2.

（2）当k=1时，得：

若a+1中无0，得：

0→1→1→0，

c（m）=2.

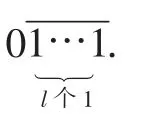
①当l为奇数时，得：

0→1→1→0，

c（m）=2.

②当l为偶数时，得：

c（m）=1.

综上所述，可得：

定理1设数列{A（n）}中第m个为0的项对应的二进制数是a（得A（a）=0），则c（m）=0，1 或 2，具体的情形是：

再研究d（m）.

记数列{A（n）}中第m个为1的项对应的二进制数是a（得A（a）=1）.

当a的末位是1时，设a的末尾连续的1恰有k（k∈N*）个.

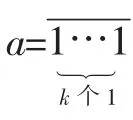
1→1，

d（m）=0.

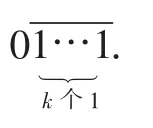
①当k为奇数时，得：

1→1，

d（m）=0.

②当k为偶数时，得：

1→0→1，

d（m）=1.

当a的末位是0时，设a的末尾连续的0恰有k（k∈N*）个.

（1）当k≥2时，得：

1→0→0→1，

d（m）=2.

（2）当k=1时，得：

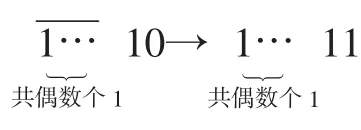
若a+1中无0，得：

1→0→1，

d（m）=1.

①当l为奇数时，得：

1→0→0→1，

d（m）=2.

②当l为偶数时，得：

1→0→1，

d（m）=1.

综上所述，可得：

定理2设数列{A（n）}中第m个为1的项对应的二进制数是a（得A（a）=1），则d（m）=0，1 或2，具体的情形是：

参考以上定理2的推导，还可得出：

定理3设数列{A（n）}中第m个为1的项对应的二进制数是a（得A（a）=1），则e（m）=1 或 2，具体的情形是：

参考以上定理1的推导，还可得出：

定理4设数列{A（n）}中第m个为0的项对应的二进制数是a（得A（a）=0），则（fm）=1或2，具体的情形是：

1.甘志国.对2011年高考湖南卷理科第16题的研究［J］.数学教学，2012（11）：45-46.

2.杜志建，主编.《金考卷特快专递》第1期·数学（文）［Z］.乌鲁木齐：新疆青少年出版社，2012.