一道高考题教学的“三退三进”

☉浙江省绍兴市稽山中学 刘智强

在数学教学中，通常会在茫茫题海中选取一些高考试题作为教学的内容，那么为何选取的是这道题？其理由是什么？如何用之，更能提升其教学价值？其方法是否具有一般可操作性？围绕上述问题，备课组进行了主题研修活动，要求教师以高考二轮专题复习为背景，以函数中的“任意性和存在性”内容为载体，利用高考试题进行教学设计、课堂展示和研讨.

一、选来选去，选中的为什么是这道题目

（2009年浙江理22题）已知函数（fx）=x3－（k2－k+1）x2+5x－2，g（x）=k2x2+kx+1，其中k∈R.

（Ⅰ）设函数p（x）=（fx）+g（x）.若p（x）在区间（0，3）上不单调，求k的取值范围；

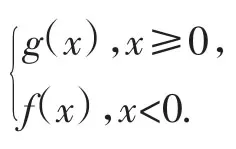
解析：（Ⅰ）略.

（Ⅱ）当x＜0时，有q′（x）=f′（x）=3x2－2（k2－k+1）x+5.

当x＞0时，有q′（x）=g′（x）=2k2x+k，因为当k=0时不合题意，因此k≠0.

下面讨论k≠0的情形，记A=（k，+∞），B=（5，+∞）.

（i）当x1＞0时，q′（x）在（0，+∞）上单调递增，所以要使q′（x2）=q′（x1）成立，只能x2＜0且A⊆B，因此有k≥5；

（ii）当x1＜0时，q′（x）在（0，+∞）上单调递减，所以要使q′（x2）=q′（x1）成立，只能x2＞0且A⊇B，因此k≤5.

综合（i）（ii）k=5.

当k=5时A=B，则∀x1＜0，q′（x1）∈B=A，即∃x2＞0，使得q′（x2）=q′（x1）成立，因为q′（x）在（0，+∞）上单调递增，所以x2的值唯一.

同理，∀x1＜0，即存在唯一的非零实数x2（x2≠x1），使q′（x2）=q′（x1）成立，所以k=5满足题意.

备课组里的教师找来找去，反复比较，最后基本统一意见，选取了这道高考试题作为这节课的核心问题进行教学.理由主要有三点：一是题目符合教学目标.既掌握函数中的“任意性和存在性”问题的解决策略，并通过问题解决的探究过程，形成会用集合观点、函数思想和数形结合方法解决函数综合问题的能力，形成一种能理解“陌生的东西”、解决压轴综合问题的数学思维和心理机制.二是题目形式创新、思维要求层次高，具有综合性.第一问中用了一个否定词“不单调”，明显比通常用“单调”要求思维更灵活更丰富，第二问用了分段函数，导函数以及陌生语句“对任意给定的非零实数x1，存在惟一的非零实数x2（x2≠x1），使得q′（x2）=q′（x1）成立”，题型就显得既平和又有新意，似曾相识而不落套.三是题目符合学生实际，具有针对性.同时在高三二轮复习中，学生薄弱的、需要提高的是解决“压轴问题”的思想和心理.这三点理由也符合高三复习教学中题目选取的一般原则，既题目具有代表性、针对性、综合性、灵活性、整体性.

二、“三退三进”，能提高复习教学的效能

所谓“三退”：一是退到与问题相关的最基本命题上来，既把原来的综合问题进行剖解、分拆、转化为若干最基本命题，弄清这些最基本命题是什么？怎么解决？二是退到与问题相关的数学核心概念、核心思想上来，既弄清问题中涉及的数学核心概念是什么？它们之间的联系是什么？怎样从数学核心思想出发进行思考问题、解决问题？三是退到“适合”学生的“问题引导学习”教学上来，用问题串、变式串来搭建“脚手架”，引导学生自主探究.

在这节课教学中，面对学生对题目语句的不理解、题目形式陌生而不知所措的情况，教师设计了一组“问题串”，退到了这类问题中的四个最基本命题，退到了这类问题涉及的数学核心概念和核心思想，并增设两个具体函数问题做铺垫，启发诱导学生自己去理解、去探究.

课堂片断1：

问题1：已知函数f（x）=2k2x+k，x∈［0，1］，函数g（x）=3x2－2（k2+k+1）x+5，x∈［－1，0］，问k=2时，对任意x1∈［0，1］，是否存在x2∈［－1，0］，使g（x2）=f（x1）成立？

教师：请你画出函数图像，并根据图像之间的关系理解题意，用图像视角作出判断.

学生：从两个图像联系上看，不一定存在.

变式1：当k=6时，对任意x1∈［0，1］，是否存在x2∈［－1，0］，使g（x2）=f（x1）成立？

教师：请你画出函数图像，求出值域，并根据值域之间的关系理解题意，用集合关系视角作出判断.

学生：f（x）的值域A=［6，78］，g（x）的值域B=［5，94］，A⊆B，所以存在.

变式2：对任意x1∈［0，1］，存在x2∈［－1，0］，使得g（x2）=f（x1）成立，求k的取值范围.

教师：请你画出函数图像，求出值域，并根据图像直观及值域之间的关系理解题意，给出解析.

学生：f（x）=2k2x+k，x∈［0，1］的值域A=［k，2k2+k］，g（x）=3x2－2（k2+k+1）x+5，x∈［－1，0］的值域B=［5，2k2+2k+10］，“对任意x1∈［0，1］，存在x2∈［－1，0］，使得g（x2）=f（x1）成立”，等价于值域A⊆B，既5≤k且2k2+k≤2k2+2k+10，所以5≤k.

变式3：存在x1∈［0，1］，x2∈［－1，0］，使得g（x2）=f（x1）成立，求k的取值范围.

变式4：对任意x1∈［0，1］，存在x2∈［－1，0］，使得g（x2）＜f（x1）成立，求k的取值范围.

变式5：存在x1∈［0，1］，存在x2∈［－1，0］，使得g（x2）＜f（x1）成立，求k的取值范围.

教师：请你尝试独立解析上述问题，并进行反思总结.

学生：变式3中的“存在x1∈［0，1］，x2∈［－1，0］，使得g（x2）=f（x1）成立”，等价于g（x）的值域与f（x）的值域的交集非空.

变式4中的“对任意x1∈［0，1］，存在x2∈［－1，0］，使得g（x2）＜f（x1）成立”，等价于gmin（x）＜fmin（x）.

变式5中的“存在x1∈［0，1］，存在x2∈［－1，0］，使得g（x2）＜f（x1）成立”，等价于fmax（x）＞gmin（x）.

学生：对函数中的存在性和任意性问题，相等关系转化为函数值域之间的关系，不等关系转化为函数的最值大小.

所谓“三进”：一是进到问题的细微之处，既具体题目有什么特殊性？题目的解决方案有什么特殊性？题目结构有什么创新性？二是进到问题的拓展变式探究处，既问题条件和结论有哪些变化？解决它们的思想方法有什么联系和不同？三是进到问题链、方法链、思维链的系统之处，既把问题、思想、方法放在一个系统内进行认识、梳理、整合，达到融会贯通，无招胜有招的境界.

在这节课的教学中，教师用“问题串”引导学生“说题”的形式，达到“三进”境地.即教师用一些诱导“怎样去思考”的框架性设问，让学生自己说解题的思考过程、具体解法、解题反思以及题目的变式联系等.

课堂片断2：

问题2：（2009年浙江理22题）

教师：面对“陌生的东西”，应“先做些什么”？

学生：画出q′（x）的图像，看看题意的几何意义，数形结合应理解题目意思，看看是否能转化为“熟悉的东西”，化归于“已经解决的东西”.

教师：这个问题与前面的“问题1”有什么联系？有什么不同？怎样解析？

学生：分段函数q′（x）的两个部分可以类似看成是问题1中的两个函数.“存在惟一”等价于“单调性”，解析略.

教师：请大家再回顾反思总结，有什么经验规律总结？有什么东西可以升华？

学生：这类问题除了与前面所说把问题转化为值域之间的关系之外，还要求考虑单调性，既由单调性得出存在唯一.解题时，可以先画出分段函数q′（x）的图像，结合图像去理解、分析、转化，事实上，因为当x＜0时，有q′（x）=f′（x）=3x2－2（k2－k+1）x+5，是单调递减，当x＞0时，有q′（x）=g′（x）=2k2x+k，单调递增，根据图像，问题就会迎刃而解.

变式1：已知函数f（x）=（2－a）（x－1）－2lnx，g（x）=xe1－x，a∈R，若对任意的x0∈（0，e］，在（0，e］，上总存在两个不同的xi（i=1，2），使得f（xi）=g（x0）成立，求a的取值范围.

变式2：（2011年浙江理22）设函数f（x）=（x－a）2lnx（a∈R），求实数a的取值范围，使得对任意x∈（0，3e］恒有f（x）≤4e2成立.

教师：请大家想一想、说一说思路，作为课后练习.

学生：会做了，思考方法一样的.变式1问题除与前面一样外，还要考虑满足“存在两个”，同样借助图像去理解就能得到问题解决的关系式.变式2问题等价转化为f（x）的最大值不大于4e2.

高考题教学的“三进三退”是一种教学策略，是从无招到有招再到无招，达到无招胜有招的一个过程，是提高教学效能的行之有效的方法，需要教师理解学生、理解数学、理解教学，需要教师共同进行“三进三退”.

1.章建跃.中学数学课改的十个论题［J］.中学数学教学参考（高中），2010，3.

2.刘智强.用“情境+问题串”引导数学课堂教学［J］.教育实践与研究（中学版），2008，2.