从“量”的视角剖析一个“一题多解”案例

☉浙江省绍兴市第一中学 徐 萍

文［1］提供了一个生动的“一题多解”案例，反复学习后，笔者认为进一步探讨：有利于我们对向量的工具性和思想方法有更深刻的理解；有助于我们对“一题多解”教学形式更好地认识与评价.本文选取“量”这一视角，对文［1］“一题多解”进行解题分析.

一、说明

文［1］的“题”是2009安徽数学卷（理）的第14题（附后）.所提5种解法具体过程本文从略，在后续讨论中适当转述.

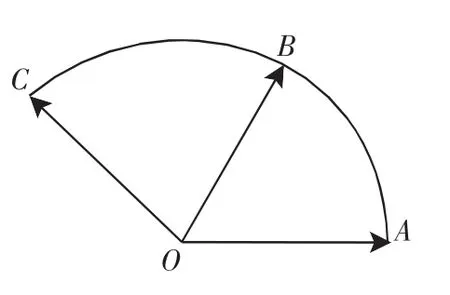
给定两个长度为1的平面向量和，它们的夹角为120°.如图所示，点C在以O为圆心的圆弧（上变动.若，其中x，y∈R，则x+y的最大值是________.

二、从“量”的视角剖析案例

数学是研究数量关系和空间形式的学科，故而从量的视角观察、分析问题及其结构关系应是一种最基本的思维模式.量是一个宽泛的概念，可以分解细化指向一些具体的数学对象和内容.

1.抓住“已知量、未知量和待求量”

抓住上述三量是解决问题的基本保障，思维展开的难点与关键是“如何从向量转入数量？”

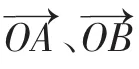
学生的问题是，没养成分析“已知量、未知量和待求量”的解题习惯，不能从整体上认识和把握问题实质；选不准问题切入口，解题盲目性大，过早陷入细节操作，从而缺乏方法选择、判断、调控的所必需的敏捷性和灵活性.从案例呈现授课教师的提问及听课老师的评说，我们感受以上的认识与引导明显缺乏.学会观察已知量、未知量与待求量，寻找它们之间的关系是整个解题活动的中心，教师的一个重要任务，正如波利亚所说：应当对对他的思路稍加渲染，而且向自己提出那些他在帮助学生时所使用的同样的一些问题.受益于这样的引导，学生最终将发现这些问题和建议的正确用法.而且通过这样去做，学生将学到一些比任何具体的数学知识更重要的东西.

2.辨清“常量、参变量和变量”

通过辨识变与不变，将问题升华为用“函数与方程观点”引领思考，对已知量、未知量和待求量作进一步分析，以“变与不变”为切入口，得到以下观察结果：对向量，，它们的模为1，夹角120°为常量虽在动，但它的模为不变量1；变量是x，y，x+y.在此基础上我们分析解法1和解法2的动机、依据和优缺点：

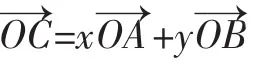
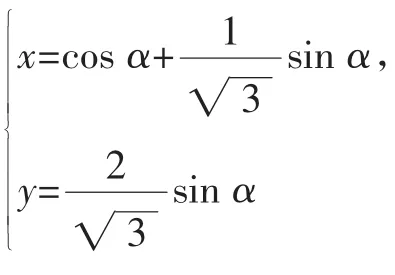
以上的思考，明显是对“已知量、未知量和待求量”进一步深入分析.

3.识别“等量、同一个量”

这是产生形式上不同表示和引入运算而不丧失相等关系的朴素观念.

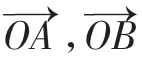
“同一个量”的概念也很重要，它有助于我们透过表象看本质，学会根据解题需要选择恰当方式表示同一量.波利亚说过“列方程的关键就在于应当清楚的认识到‘一个方程就是用两种不同的方式去表示同一个量’”.解法3中对的坐标表示就体现了这一观念，而解法5对两边“作数量积”也有这层味道.

以上分析，等量和同一个量的视角选取，有助于我们灵活选择量的表示、对量实施恰当的运算变形，而它们都是解决问题的重要思维步骤，对形成朴素的、一般意义的数学观也很重要.

4.把握“基向量、基本量”

将复杂关系以简单、统一观点处理，对“量x，y”几何意义的追问使我们获得新发现.

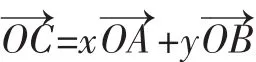
也正是基于对“量x，y”几何意义的追问，笔者对文［1］“缺憾”之“细节的处理不够精准，形成误解”提出两点看法：（1）解法4学生丁的图4和修正后的图6其实或多或少都有点问题，它不足以全面反映向量在基向量，方向分解效果，得到的只是α取特定值时平行四边形（或三角形），需要指出的是，当点C运动到圆弧（中点时，也即α=60°最为特殊（变化界点），得到的平行四边形就是OACB，图4适当调整，可以刻画α＞60°情形，而图6是刻画α＜60°情形，若要全面观察运动变化效果，最好借助信息技术演示；（2）文［1］对原授课教师变式问题没有理解好，限制条件，对“点C在△ABC的内部（包括边界）”是正确的，而改为是错的，它只是对“点C在扇形域OAB的内部（包括边界）”的范围的一种初步刻画，而且还存在问题：因为x，y之间是具有相互约束关系的，譬如当x=0.5时，y的取值还是0≤y≤吗？进而笔者提出一个新问题：将文［1］中变式“点C在△ABC的内部（包括边界）”改为“点C在扇形域OAB的内部（包括边界）”，试问动点M（x，y）所构成的区域面积如何解决.笔者觉得用初等方法难以实现，不知各位有何高招？请不吝赐教！

1.缪荷芳.一节高三“一题多解”课的听课感悟［J］.中学数学教学参考（上旬），2012，1-2.

2.张奠宙，柴俊.欣赏数学的真善美［J］.中学数学教学参考（上旬），2010，1-2.

3.罗增儒.课例反思时时有，教师发展步步高——教学应是一种学术活动［J］.中学数学教学参考（上半月），2008，1-2.