6－UPS并联机床位姿空间图谱

陈小岗 孙 宇 刘远伟 吴海兵

1.南京理工大学，南京，210094 2.淮阴工学院，淮安，223003

0 引言

与传统结构形式的数控机床相比，采用Stewart平台结构形式的六自由度纯并联机床被认为存在工作空间与机床体积之比较小，工作空间内各点的姿态能力、误差、刚度等特性不一致的缺点［1-3］。但该类型机床的工作空间与体积之比小至何种程度，工作空间内各点的姿态能力不一致到何种程度，具有什么样的分布特性，目前鲜有具体而详尽的数据佐证。

吴海兵等［4］对Stewart型并联机床的工作空间进行了分析计算，获得了可达空间呈陀螺状的结论，并给出了圆柱体的推荐工作空间，但未给出两者相对于机床体积的比值，且未对姿态能力进行研究。赵迎祥等［5］对6－SPS并联机床工作空间进行分析时，考虑了动平台的姿态问题，并研究了工作空间随自转角的变化情况。张曙等［1］对姿态角对工作空间的形状、大小、位置等特性的影响进行了研究，此外文献［6-12］对Stewart型并联机构进行了运动学正解、位置奇异、姿态奇异、自运动等问题的研究，但它们均未给出工作空间内姿态能力的具体分布特性。

综合目前的研究现状，本文从杆长约束、转角约束、干涉约束出发，首先对交叉杆式Stewart型并联机床进行了平动工作空间计算，并求取了其最大包容球、最大包容圆柱、最大包容长方体。然后重新定义了“姿态能力角”这一概念，计算了该机床平动工作空间内各点处的姿态能力角，绘制了姿态能力角分布图谱，获得了与刀轴偏摆能力相应的姿态空间。不但更全面地评价了工作空间与机床体积之比，而且获得了姿态空间具体而详细的分布特性。本文的研究结果更全面地揭示了并联机床的加工范围及加工能力。

1 BJ－04－02(A)并联机床运动学模型

1.1 并联机床结构简图

本文的研究对象为BJ－04－02(A)并联机床，其进给机构采用6－UPS交叉杆式Stewart平台变型结构，其中，U副(虎克铰)用轴线垂直相交的2个转动副等效替代，S副(球铰)用轴线两两垂直且相交于一点的3个转动副等效替代。机床的三维模型及实际结构如图1所示。

图1 BJ－04－02(A)并联机床

在该机床上定义2个坐标系:①惯性坐标系OA XYZ，其原点在定平台上铰点分布平面的中心，其X轴平行于铰点A4指向A3的方向，Z轴竖直向上;②随动坐标系OB X'Y'Z'，其原点在刀具平台几何中心，X'轴平行于铰点B5指向B3的方向，Z'轴垂直于刀具平台表面向上，如图2所示。

图2 机床结构简图

铰点Ai(i=1，2，…，6)在惯性系中的位置矢量记作ai，铰点Bi在随动系中的位置矢量记作bi。随动系的原点OB在惯性系中的位置矢量记作rB。随动系在惯性系中的方向余弦矩阵为R。由Ai指向Bi的杆矢量记作Li。上述各矢量间的关系为

1.2 工作空间的约束条件

在求解并联机床工作空间时，主要考虑杆长约束、铰链转角约束、驱动杆之间的干涉约束［4-5］。

(1)杆长约束。机床的6根驱动杆均有各自的伸缩范围(极小值与极大值分别为Lmin、Lmax)。当刀具平台在工作空间内运动时，6根杆的长度|Li|必须满足

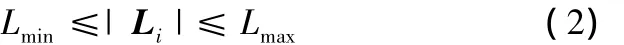
(2)转角约束。该机床的每条支链均有5个转动副，按从定平台到刀具平台的顺序，第2、第4转动副有转角范围限制，即驱动杆中心轴线与第1、第5转动轴线之间的夹角φ有范围限制，记其下限值为φmin。当刀具平台在工作空间内运动时，φ必须满足

(3)干涉约束。6根杆均为圆柱体，其半径记为R。当刀具平台在工作空间内运动时，6根杆的中心轴线之间的距离Dij(i，j=1，2，…，6，且i≠j)必须满足

2 位置空间

并联机床的工作空间有最大空间、定向空间、完全空间之分。最大空间是指刀具平台以任意姿态可达点的集合。定向空间是指刀具平台以指定姿态可达点的集合。完全空间是指刀具平台以所有姿态均可达点的集合。定向空间和完全空间都是最大空间的一个子集。

2.1 位置空间

使固结于刀具平台的随动系的X'、Y'、Z'轴始终分别平行于惯性系的X、Y、Z轴，在该参考姿态下，刀具平台作平动可达点的范围即为本文所称的位置空间。此时矩阵 R=I3×3，则式(1)简化为

其中，矢量ai和bi可从表1、表2获得。

表1 定平台铰点位置参数表 mm

表2 动平台铰点位置参数表 mm

经初步计算后，判定工作空间在x∈［－500，500］mm，y∈ ［－500，500］mm，z∈ ［－1400，－400］mm范围内。对该长方体形空间，按照X向间隔10mm、Y向间隔10mm、Z向间隔20mm进行采样取点。

对每一个采样点，将其位置坐标赋予矢量rB，然后根据式(5)计算各驱动杆的轴线方向及杆长，并根据式(2)～式(4)分别判断是否满足杆长、转角、干涉约束。

在对所有采样点进行计算、判断后，获得平动可达位置空间，如图3所示。该位置空间由Z方向上的一系列片层组成，为直观地体现其立体形状，按照Z坐标“由小到大”的顺序绘制Z向各层的位置点。

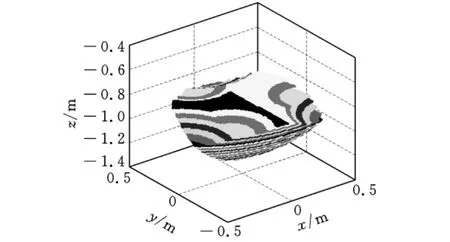
图3 位置空间

图3所示的位置空间包含点数为67 434，占据的体积约为 0.135m3。机床外围体积约为5.86m3，因此该空间与机床体积之比约为2.30%。

Stewart型并联机床不仅工作空间的绝对体积小，而且其与机床体积之比，较之传统机床，也是较小的。相关研究均证实了这一定性结论，但给出定量数据的很少，且不够全面。本文基于上述计算结果，给出并联机床位置空间的相关数据，并将其与串联式五轴加工机床进行对比。

2.2 包容球、包容圆柱、包容长方体

图3所示的位置空间上阔下尖，虽然其在XY平面内的投影具有一定的三角对称性，但并不是严格的规则形体。在利用该机床进行加工的过程中，图3所示的空间并不能完全得到利用，一般取其所能包容的最大球、最大圆柱或最大长方体作为常用工作空间，这三类包容体的中心点位置、几何尺寸、体积及与机床体积(5.86m3)之比如表3所示。具体工作空间如图4所示。

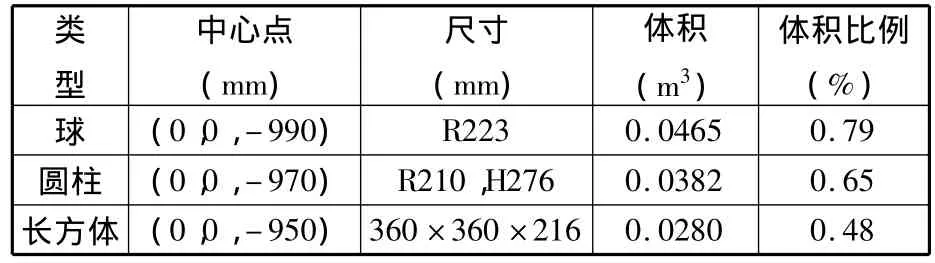
表3 三类包容体参数表

Mikron五轴加工中心UCP800是传统串联结构形式的机床，其五轴为X、Y、Z、A、C，具有曲面加工能力，其外围体积约为7.73m3，由X、Y、Z三个方向的行程获得其常用工作空间为0.26m3，与机床体积之比为3.36%。

图4 三种规则形状的常用工作空间

与表3对比可见，BJ－04－02(A)并联机床的常用平动位置空间与机床体积之比仅为传统结构形式机床的1/7～1/4。

3 姿态能力角及相应的方向余弦矩阵

式(1)中的方向余弦矩阵含有9个参数，用于描述物体的空间方向和姿态时直观性较差，因此常用3个角度来描述物体的空间方向和姿态，如起源于航船姿态描述的“滚动、俯仰、偏航”RPY角以及广泛应用于航海天文的“进动、章动、自旋”欧拉角等［13-14］。

3.1 姿态能力角

“进动、章动、自旋”欧拉角可描述物体的空间任意姿态，尤其适于描述陀螺的运动，但在机床控制中，由于需约束刀具平台发生绕刀轴的自旋，因此需约束自旋角使其始终等于进动角的负值。

本文采用绕基础坐标系XY平面内与X轴成角度ψ的轴线旋转θ角来描述机床刀具平台的姿态，这种姿态描述方法直观性更强，也更简便，如图5所示。

图5 刀轴偏摆示意图

在保持刀尖点不动，利用刀具平台的姿态能力实现刀轴偏摆时，刀轴的偏摆范围是以基础坐标系的Z轴为轴线的倒锥形(锥尖在下，锥底面在上)。该倒立圆锥的半锥顶角(θ角)表征了刀轴的偏摆能力。

姿态能力角:在以Z轴为轴线的360°范围内各方向上，刀轴可达最大偏摆角的最小值。换言之，即在以Z轴为轴线的360°范围内，刀轴向各个方向偏摆均可达的角度的最大值。

3.2 方向余弦矩阵

根据上述(ψ，θ)姿态描述方法，式(1)中的方向余弦矩阵形式如下［15］:

其中，α、β、γ 为旋转轴线与基础坐标系X、Y、Z轴的夹角，且α=ψ，β=π/2－ψ，γ=π/2。

4 姿态空间图谱

对于图3所示的位置空间内每一点，假设刀具平台中心处于该点，在杆长、转角、干涉约束下，计算刀具平台的姿态能力角，并利用MATLAB绘制其在工作空间内的分布，如图6所示。

图6 姿态能力角分布图

图6中，按照位置空间内各点的Z坐标“由小到大”的顺序绘制Z向各层的姿态能力角分布。

依据图6所示的计算结果，在X、Y、Z方向分别取离散片层，可获得各层内姿态能力角的分布情况。图7所示分别为3个离散层(x=－100mm，y= －60mm，z= －880mm)的姿态能力角等值图。

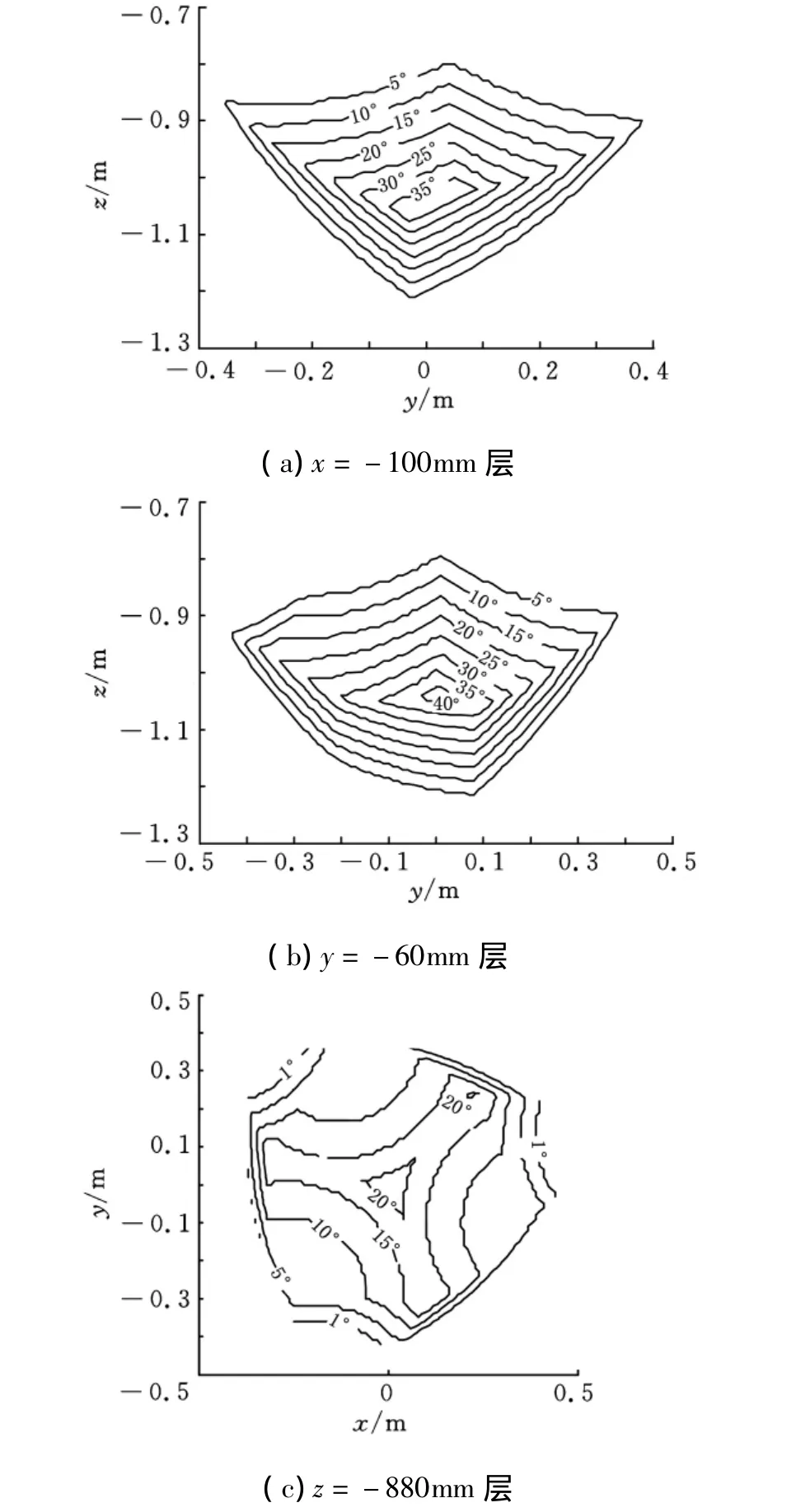
图7 三个离散层上的姿态能力角等值图

依据图6所示的计算结果，可获得任意给定的姿态能力角所对应的工作空间。分别取姿态能力角为 5°、15°、25°，相应的可达工作空间及其最大包容球如图8所示。

姿态能力角分别取为 5°、10°、15°、20°、25°时，对应工作空间最大包容球、最大包容圆柱及最大包容长方体的相关参数如表4所示(机床体积为5.86m3)。

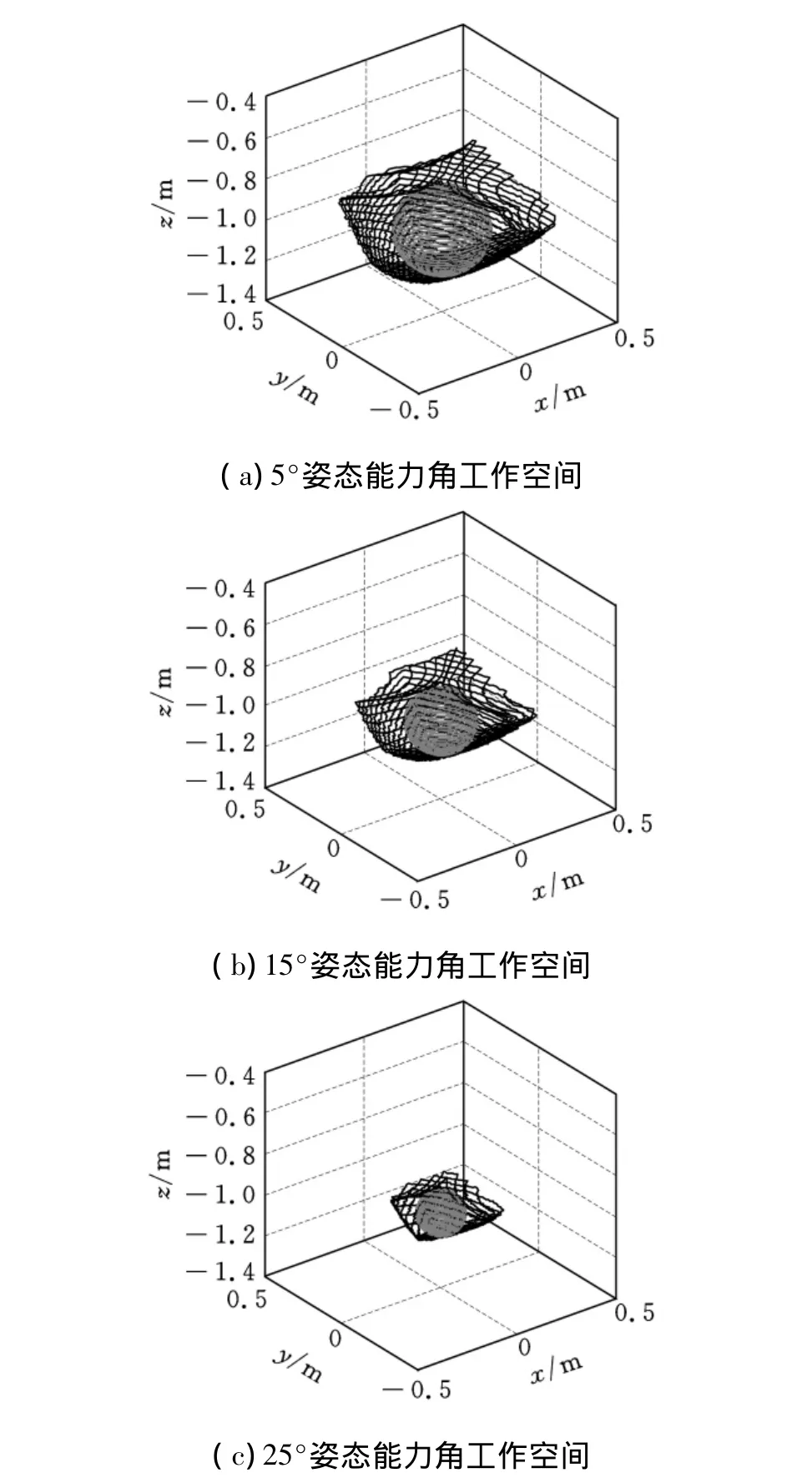
图8 三个姿态能力角对应的工作空间

表4 5°～25°工作空间包容体参数表

与UCP800相比，5°姿态能力角对应的常用工作空间与机床体积之比约为UCP800的1/8～1/6，20°姿态能力角对应工作空间与机床体积之比约为 UCP800的1/28～1/22，25°时则仅为1/56～1/48。

5 结论

(1)该机床的工作空间呈陀螺形，上阔下尖，不是严格的规则体，但其在XY平面内的投影有一定的三角对称性。

(2)参考姿态下，该机床的可达位置空间与机床体积之比约为2.30%。但对于规则形状(球、圆柱、长方体)的位置空间，该比值仅为UCP800的1/7～1/4。5°姿态能力角对应的常用工作空间与机床体积之比仅为UCP800的1/8～1/6，20°姿态能力角时该比值仅为UCP800的1/28～1/22。

(3)在可达位置空间内，各点处姿态能力角的分布具有如下特性:在中心区域，刀具平台的可达偏角较大，越接近边缘区域，可达偏角越小。

［1］张曙，Heisel U.并联运动机床［M］.北京:机械工业出版社，2003.

［2］于大泳，韩俊伟，李洪人.并联机器人位姿误差分析［J］.哈尔滨商业大学学报(自然科学版)，2004，20(3):278-280.

Yu Dayong，Han Junwei，Li Hongren.Study on Pose Errors Analysis of Parallel Robot［J］.Journal of Harbin University of Commerce(Natural Science Edition)，2004，20(3):278-280.

［3］李育文，张华，杨建新，等.6－UPS并联机床静刚度的有限元分析和实验研究［J］.中国机械工程，2004，15(2):112-115.

Li Yuwen，Zhang Hua，Yang Jianxin，et al.Finite Element Analysis and Experimental Study for the Stiffnessofa6－UPSParallel Kinematic Machine［J］.China Mechanical Engineering，2004，15(2):112-115.

［4］吴海兵，刘远伟，左敦稳.交叉式并联机床工作空间分析［J］.机械科学与技术，2009，28(4):472-475.

Wu Haibing，Liu Yuanwei，Zuo Dunwen.Workspace A-nalysis of a Cross － legged Parallel Machine Tool［J］.Mechanical Science and Technology，2009，28(4):472-475.

［5］赵迎祥，鲁开讲，郭旭侠，等.6－SPS并联机床工作空间分析［J］.机械设计，2005，22(8):37-39.

Zhao Yingxiang，Lu Kaijiang，Guo Xuxia，et al.Analysis on Working Space of 6－SPS Parallel Machine Tools［J］.Journal of Machine Design，2005，22(8):37-39.

［6］Cheng Shili，Wu Hongtao，Wang Chaoqun，et al.A Novel Method for Singularity Analysis of the 6－SPSParallel Mechanisms［J］.Science China，2011，54(5):1220-1227.

［7］Cheng Shili，Wu Hongtao，Wang Chaoqun，et al.The Forward Kinematics Analysis of 6－3 Stewart Parallel Mechanisms［J］.Intelligent Robotics and Applications，2010，6424:409-417.

［8］Cao Yi，Zhou Hui，Shen Long，et al.Singularity Kinematics Principle and Position－Singularity Analyses of the 6 － 3 Stewart－ Gough Parallel Manipulators［J］.Journal of Mechanical Science and Technology，2011，25(2):513-522.

［9］Cao Yi，Zhang Qiuju，Zhou Hui，etal.Property Identification of 6－3 Stewart Parallel Manipulators for Special Orientations［J］.Intelligent Robotics and Applications，2008，5314:36-45.

［10］Li Baokun，Cao Yi，Huang Zhen，et al.Orientation －singularity and Orientation－workspace Analysis of the Stewart Platform Using Unit Quaternion［J］.Intelligent Robotics and Applications，2008，5314:131-140.

［11］Wu Peidong，Wu Changlin，Yu Lianqing.An Method for Forward Kinematics of Stewart Parallel Manipulators［J］.Intelligent Robotics and Applications，2008，5314:171-178.

［12］Karger A.Self－ motions of 6 －3 Stewart－ Gough Type Parallel Manipulators［M］//Lenarcic J，Stconistic M M.Advances in Robot Kinematics:Motion in Man and Machine.Dordrecht:Springer Nether Lands，2010:359-366.

［13］黄田，汪劲松.Gough_Stewart平台运动学设计理论与方法［J］.中国科学(E 辑)，1999，29(4):310-320.

Huang Tian，Wang Jingsong.Theory and Method of Kinematics Design for Gough_Stewart Platform［J］.Science in China(Series E)，1999，29(4):310-320.

［14］黄真，赵永生，赵铁石.高等空间机构学［M］.北京:高等教育出版社，2006.

［15］韩建友.高等机构学［M］.北京:机械工业出版社，2004.