考虑空位缺陷的单晶硅纳米级磨削过程的分子动力学仿真

郭晓光 张 亮 金洙吉 郭东明

大连理工大学精密与特种加工教育部重点实验室，大连，116021

0 引言

目前在机械加工领域，分子动力学仿真研究的对象几乎都是无缺陷的理想晶体，没有考虑材料实际存在的微小缺陷，也没有涉及复杂的物理化学过程［1-5］。实际加工的材料即使经过化学机械抛光，仍然或多或少存在一些空位、间隙原子、位错等缺陷，并且材料的性能在很大程度上取决于其内部的缺陷，因此材料内部缺陷对加工过程的影响不容忽视［6］。另外，材料内部缺陷在超精密加工过程中受切削力、切削热等的作用会逐渐发展变化，如微裂纹和微孔洞的形核、扩展和汇合，从而导致材料的微观结构发生不可逆的热力学耗散过程，造成材料表面、亚表面的损伤。因此，对考虑缺陷的单晶材料超精密加工过程进行分子动力学仿真将使分子动力学方法更具有实际应用意义。

本文建立了考虑空位缺陷的单晶硅磨削过程分子动力学仿真模型，并进行了仿真计算，分析了材料的变形、相变等，研究了超精密磨削加工机理中的一些重要问题。

1 分子动力学仿真

1.1 考虑空位缺陷的单晶硅磨削过程分子动力学仿真模型

单晶硅磨削过程的三维分子动力学模型如图1所示。磨粒为金刚石原子，仿真中认为磨粒是绝对刚性的，即不因外力作用而变形磨损。工件为单晶硅原子，仿真中，工件被分为牛顿层、恒温层和固定边界层［7］。牛顿层的原子运动可由牛顿方程来描述;恒温层的引入是为了使磨削过程中产生的热量及时传导出去，通过不断标度原子速度保持该区域温度恒定;固定边界层的原子始终保持不动，起到减小边界效应的作用，其内部原子在仿真过程中不参与计算。

图1 磨削过程分子动力学仿真模型

随机剔除原子来构建相应的带点缺陷的单晶硅模型，在工件原子中剔除0.5%的原子，形成相应的空位。存在的点缺陷会对晶体结构产生一定的影响。基于第一性原理，本文采用Material Studio中的CASTEP(Cambridge sequential total energy package)模块来验证所构建模型的可行性。CASTEP是Cerius2和Materials Studio的量子化学模块之一，用密度泛函理论模拟固体、界面和表面的特性，是一种非常有效的研究点缺陷(空位、间隙、置换杂质)和扩展缺陷(晶界和位错)的性质的模块。图2所示为无缺陷硅晶体的晶胞和存在一个点缺陷的硅晶体晶胞。理想晶体结构硅晶体的参数为:晶胞棱长a=b=c=0.543nm，夹角α=β=γ=90°。经过CASTEP模块的计算，存在一个点缺陷的晶胞的参数为:a=b=c=0.547nm，与理想晶格参数比较，偏差小于0.005nm;α=90.01254°，β = γ =89.98746°，偏差小于 0.005°。可知，当点缺陷不大时，可以近似认为晶体的结构没有发生变化，所以可以采用随机剔除原子的方法构建含点缺陷的单晶硅模型。

图2 无缺陷和有空位缺陷的硅晶体晶胞结构

1.2 势函数的选取和力的计算

单晶硅是金刚石型晶体结构，对硅原子势能的计算应考虑多原子价键之间的相互影响因素，故采用多原子系统的Tersoff势函数u(rij)［8］对单晶Si－Si和金刚石C－C以及Si－C进行计算，公式如下:

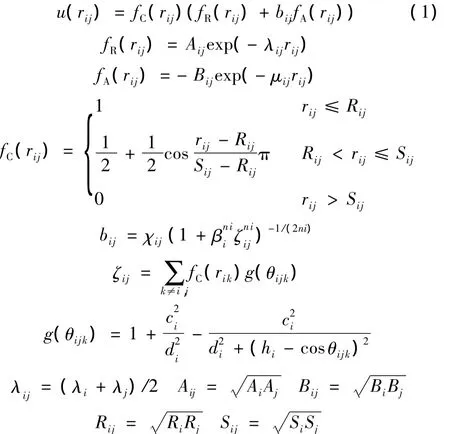
其中，u(rij)为原子i与原子j之间的势函数;fC(rij)为截断函数;fR(rij)为排斥项函数;bij为低价函数，fA(rij)为吸引项函数;rij为原子i与原子j之间的距离;θijk为原子i、j、k之间的夹角。其他参数的值见表1。

表1 Tersoff势函数参数

势函数确定以后，原子之间的作用力Fij就可以通过势函数对rij求导得出，即

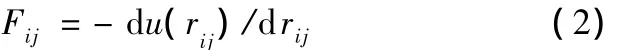
作用在第i个原子上的总原子力等于其周围所有原子对该原子作用力的合力，即

1.3 系统的运动方程

由统计物理可知，对于一个由大量粒子组成的物理系统，其宏观特性是这些粒子运动状态的综合反映，因此，分子动力学仿真的核心问题就是要计算所有粒子的运动规律和轨迹，故可假设系统中的每个原子都各自服从经典牛顿力学规律，可直接用牛顿运动方程来描述:

式中，vi、ri分别为粒子i的运动距离和速度;t为时间;m为原子的质量。

建立了上述模型后，根据现有计算机的能力，选择适合的计算量，编制分子动力学计算机仿真程序，仿真结果主要以三维形式显示，工件尺寸为10nm×10nm×10nm，磨粒半径为1.8nm，仿真温度为293K，磨粒速度为20m/s，时间步长为1fs(10－15s)，磨削深度为0.5430nm。

2 考虑空位缺陷的单晶硅磨削过程分子动力学仿真结果分析

2.1 温度分析

在模拟过程中，系统初始状态设置为293K。模拟过程先对系统进行弛豫，使系统达到平衡状态，然后再进行磨削过程的分子动力学仿真［9］。图3所示为磨削前进行的16ps(1ps=10－12s)弛豫过程中的系统温度变化曲线。初始状态时，系统温度急剧下降，在0.7ps左右时达到温度最小值(约118K)。随后系统温度逐渐上升，至10ps左右达到相对稳定值，随后系统温度在此附近振荡，波动幅度小于2K。随着温度的波动减小，系统逐渐进入平衡状态。温度初期的急剧变化一方面是由于初始模型是按照理想晶体结构模型构建的，存在一定的结构不稳定;另一方面由于工件中存在边界层和自由表面，部分原子在弛豫过程中会重新排列，相互作用力较大。最终，系统通过恒温层的温度控制，在弛豫过程中逐渐达到平衡状态。

图3 弛豫过程中温度的变化

磨削过程中系统牛顿层的温度变化如图4所示，磨削初始状态时系统的温度约为293K，随着磨削过程的进行，金刚石磨粒开始逐渐接触挤压工件，原子间相互作用力增大，牛顿层的温度急剧上升。随着磨粒完全接触挤压工件，温度上升趋势变缓慢，逐渐趋于稳定，最终达到稳定切削温度。这个过程可以理解为:当磨粒开始接触工件后，磨粒与工件相互作用加剧，系统能量逐渐升高，原子间剧烈的相互作用使得牛顿层的温度迅速升高;当磨粒完全接触工件后，恒温层的调控作用使温度上升趋势变缓，通过调控作用，牛顿层温度逐渐达到较为平稳的切削温度。在整个过程中，温度出现波动的原因来自于硅晶体中存在的少量点缺陷。在磨削过程中，新的原子进入空位处，吸收大量能量，形成新的晶体结构。恒温层的温度如图5所示，在仿真中恒温层的初始温度为293K，恒温层的温度采取每10fs一标定的方法，波动范围为283～303K，恒温层用来调控系统的温度。

图4 牛顿层温度

图5 恒温层温度

2.2 势能分析

图6所示为弛豫过程中硅原子间势能变化曲线，在弛豫过程中，系统的能量首先急剧增加，然后迅速降低，在恒温层的调控下又逐渐增加，经过不断的调控，系统的能量趋于稳定。这个现象可以解释为:初始模型在结构上存在大量空位点，这种不稳定结构会导致系统初期原子的剧烈振动。随着系统自身不断的调控，部分原子重新排布，最终达到稳定状态。图7所示为考虑空位缺陷的单晶硅纳米级磨削加工过程的硅原子间势能变化曲线，结果表明:随着金刚石磨粒逐渐挤压切削工件，磨削面积逐渐增加，产生塑性变形，导致硅原子间的势能急剧增加，并伴有一定的往复波动;当磨粒完全接触工件后，系统的能量逐渐趋于稳定，硅原子间势能增加缓慢。磨粒与工件不断相互作用，大量能量以晶格应变能的形式贮存在单晶硅的晶格中，转化为硅原子间的势能，从而导致系统势能逐渐增加。在磨削过程中，原子间势能的反复波动主要是由单晶硅晶格的变形、晶格重构及非晶相变造成的。共价键晶体中位错的发生和运动要克服高能势垒，会导致能量的增减，而图7中势能变化仅有很小的波动，所以带缺陷的单晶硅的纳米级磨削加工过程中没有出现明显的位错。

图6 弛豫过程势能变化曲线

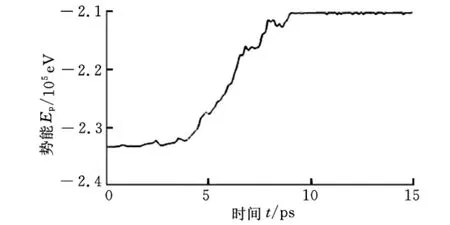
图7 加工中势能变化曲线

2.3 工件受力分析

磨削力是理解磨削过程的一个重要物理参数，它清晰反映了材料的去除过程。纳米级磨削过程中磨削力的来源与宏观磨削过程中磨削力的来源有很大区别:宏观磨削过程中的磨削力是磨削过程中产生的切削力和摩擦力的总和;纳米级磨削过程中磨削力的来源很简单，主要来源于单晶硅原子和金刚石磨粒原子之间的相互作用力。

图8所示为考虑空位缺陷的单晶硅纳米级磨削过程中，工件在X、Y、Z方向的受力曲线，从仿真结果看，X方向的力在波动中逐渐增加，然后趋于稳定，Y、Z方向的力仅在一定范围内波动。通过力的变化分析可知，X方向的力在纳米级磨削过程中起主要的切削作用，即磨粒的推挤作用在纳米级磨削过程中占主导地位，材料的去除依赖于磨粒的推挤。在磨削过程中，工件原子晶阵在磨粒的推挤作用下发生原子键断裂，原子晶格被破坏，形成非晶层。部分原子在磨粒Y方向力的作用下与已加工表层断裂的原子键结合，重构形成已加工表面的变质层。处在磨粒前方的原子在磨粒的推挤作用下，被去除掉，形成切屑。从图8可以看出，X、Y、Z方向的力都在往复波动，有些地方波动很剧烈。力的这种波动与晶格的变形、晶格重构和非晶相变有密切关系。当磨削力增大并超过原子之间结合力临界值且不足以形成位错时，原子点阵被破坏，导致原子键断裂，成为非晶态原子。此时，磨削力会出现陡降至一个较低水平的波动，而且这种作用力的波动在整个磨削过程中不断重复，因此可以认为这是由非晶相变而产生的作用力波动现象。

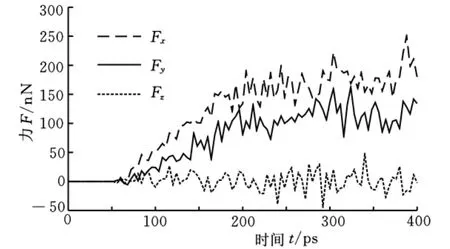
图8 工件X、Y、Z方向受力曲线

2.4 磨削过程分析

磨削过程中瞬间原子位置如图9所示。初始位置时，磨粒并未与工件接触;5ps时，磨粒部分挤压工件，使工件受挤压处原子重新排布;10ps时，磨粒已经完全作用于工件，部分工件原子已经离开工件表面，堆积在磨粒前部。但由于磨削长度较短，故并未堆积成切屑;15ps时，随着加工面积增大，在刀具前方堆积成切屑，如图9d所示。综上所述，带缺陷的单晶硅纳米级的磨削过程可以解释为:随着磨粒逐渐向单晶硅片的挤压，与金刚石磨粒接触的最外层硅原子与金刚石原子间的作用力由引力转化为斥力，同时外层原子又受到内部硅原子的作用力。相比较排斥力，内部作用力比斥力小，故斥力占主导地位。在磨粒的排斥作用下，磨粒下方的硅晶格发生了挤压变形。随着金刚石原子与硅原子之间距离的不断减小，原子间的斥力增大，大量能量以晶格应变能的形式贮存在单晶硅的晶格中，因而此能量也随着力的增大而不断增加。当贮存在变形晶格中的应变能超过一定值且不足以形成位错时，硅的原子键就会断裂，规则的晶格结构将被打破，原子排列逐渐变为无序状态(非晶态)，形成非晶层。另一部分原子离开原位置，堆积在金刚石磨粒的前方形成切屑。

当磨粒继续向前加工逐渐离开带缺陷的单晶硅时，与金刚石磨粒接触的最外层硅原子和金刚石原子间的作用力由斥力慢慢转化为引力，同时它们又受到内部硅原子的作用力，使非晶层的原子重构，释放了部分能量，从而达到新的平衡状态。如图9e所示，被挤压下去的原子会出现一定的回弹，已加工表面并未形成一层平整的“磨痕”。在形成“磨痕”过程中，“磨痕”两侧也不会产生大量侧向原子。这是由于硅是脆性材料，其脆性较大而断裂韧性又较小，材料的弹性极限和强度相差不大。

图9 磨削过程中瞬间原子位置图

2.5 空位缺陷对加工的影响

硅晶体中存在的空位缺陷会对加工中系统温度的变化和加工表面的质量有一定的影响。图10 所示分别为含0.5%、1.0%、1.5% 空位的缺陷硅晶体加工过程中系统温度的变化曲线。加工初始的阶段，三条曲线接近于重合，随着加工的进行，含空位越多的系统温度变化越小。当模拟到40ps时，系统温度随着空位数目的增加而逐渐降低。这是由于在模拟过程中，空位的存在会吸收大量的热，空位越多，吸收的热量越多，系统的温度上升越慢。另一方面，空位的存在会在一定程度上影响到加工表面的质量。含0.5%、1.0%、1.5%空位的晶体加工表面的回弹量分别为0.15nm、0.12nm和0.10nm。出现回弹是由于在磨粒推挤过程中，工件表层部分原子向下运动，形成非晶结构;失去磨粒作用后，此部分原子会受到原有晶格原子的作用，脱离晶格，在晶格上方重新形成已加工表面。在表层原子向下运动过程中，部分原子由于空位的存在，会进入空位处，到达新的平衡状态。当失去磨粒作用后，原子的回弹量将会在一定程度减小。

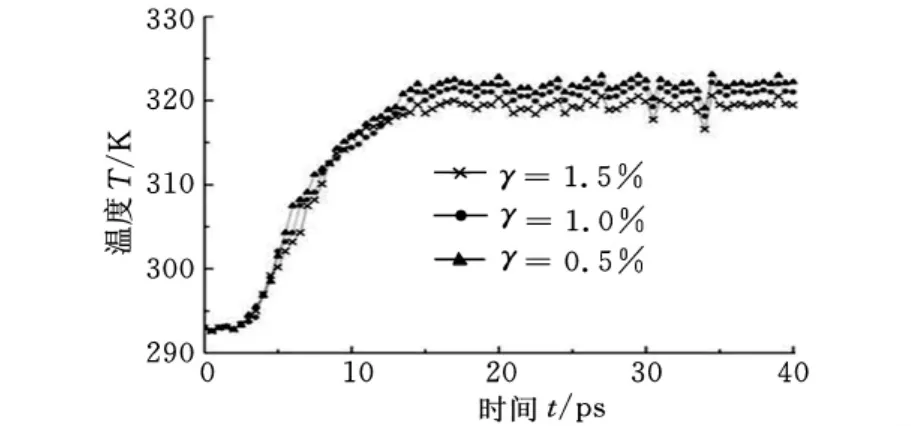
图10 不同空位数γ的系统温度曲线

整个模拟加工过程中，空位缺陷的存在并未对加工过程中切削力的变化有较为明显的影响。同时，在纳米级仿真过程中，空位缺陷对加工表面质量的影响不大。

3 结论

(1)基于第一性原理，建立并验证了含空位缺陷的单晶硅磨削过程的分子动力学仿真模型。

(2)材料的去除过程可解释为:在磨粒的推挤作用下，工件发生变形，去除原子堆积在磨粒的前方;当贮存在变形晶格中的应变能超过一定值时，材料表面的原子键断裂，即完成了材料的去除。

(3)磨削过程中，磨粒前下方的硅晶格在磨粒的压应力作用下发生了变形，当贮存在变形晶格中的应变能超过一定值且不足以形成位错时，硅的原子键断裂，晶格被打破，变为无序状态，形成了非晶层。随着磨粒不断前移，损伤层逐渐向前、向深处扩展，造成了单晶硅亚表面的损伤;同时，部分非晶层原子在压应力的作用下与已加工表层断裂的原子键结合，重构形成已加工表面变质层。磨削过程中，无明显的位错、裂纹等产生。

(4)磨削过程中，工件X、Y和Z方向的受力及硅原子间势能都是往复波动的，在空位集中处会出现较大波动。力和势能的这种波动与晶格的变形、晶格重构和非晶相变有密切关系。

(5)空位缺陷数目会影响到加工过程中温度的变化，从而在一定程度上会影响连续加工的稳定性。空位的存在会减小加工后表面的回弹，但对加工表面质量的影响较小。

［1］Tanata H，Shimada S，Higuchi M，et al.Mechanism of Cutting Edge Chipping and Its Suppression in Diamond Turning of Copper［J］.Annals of the CIRP，2005，54(1):51-54.

［2］Komanduri R，Raff L M.A Review on the Molecular Dynamics Simulation of Machining at the Atomic Scale［J］.Proceeding of the Institution of Mechanical Engineering，Part B:Journal of Engineering Manufacture，2001，215(12):1639-1672.

［3］Tanata H，Shimada S，Anthony L.Requirements for Ductile－mold Machining Based on Deformation Analysis of Mono－crystalline Silicon by Molecular Dynamic Simulation［J］.Annals of the CIRP，2007，56(1):53-56.

［4］Han X S，Lin B，Yu S Y，et al.Investigation of Tool Geometry in Nanometric Cutting by Molecular Dynamics Dimulation［J］.Journal of Materials Processing Technology，2002，129(1/3):105-108.

［5］于思远，林滨，韩雪松，等.分子动力学仿真技术在超精密加工领域中的应用［J］.中国机械工程，2002，13(1):22-25.

Yu Siyuan，Lin Bin，Han Xuesong，et al.The Application of Molecular Dynamics Simulation to Ultraprecision Machining［J］.China Mechanical Engineering，2002，13(1):22-25.

［6］Shimada S，Tanaka H，Ikawa H.Atomistic Mechanism of Surface Generation in Micromachining of Monocrystalline Silicon［C］//Proceeding of the 1st International Euspen Conference.Bremen，1999:230-233.

［7］张伟文，郭钢，黄云，等.纳米磨削磨屑形成分子动力学仿真研究［J］.中国机械工程，2011，22(2):127-131.

Zhang Weiwen，Guo Gang，Huang Yun，et al.A Molecular Dynamics Study of Chip Formation on Nanogrinding Processes［J］.China Mechanical Engineering，2011，22(2):127-131.

［8］Tersoff J.Modeling Solid － state Chemistry:Interatomic Potentials for Multicomponent System［J］.Physics Review B，1989，41:5566-5568.

［9］CheongW CD，Zhang L C.Molecular Dynamics Simulation of Phase Transformations in Silicon Monocrystals due to Nano － indentation［J］.Nanotechnology，2000，11(3):173-180.