基于VAPID的道路清障车扶正控制研究
吕成绪 张为公 李 旭
1.东南大学,南京,210018 2.南京农业大学,南京,210031
0 引言
道路清障车是交通事故救援的主要装备。扶正作为道路清障车的主要功能,是影响道路交通事故救援效率的关键因素。目前国内对道路清障车的研究主要集中在结构设计方面[1-7]。与道路清障车扶正系统类似的汽车起重机起升系统的研究,主要面向其伸缩臂控制及二次起升问题[8-10],而针对扶正控制的研究成果较少。
国内道路清障车主要配备双卷扬[11-12],国外多为四到六个卷扬。清障救援作业时,由清障救援人员手动控制、协调各卷扬位移,实现事故车辆扶正[13-16]。扶正过程中,具体操作因清障救援人员经验而异,缺乏规范,自动化程度低,严重影响救援效率。采用双卷扬扶正时,捆扎复杂,且不能保证扶正过程的稳定性,容易引发二次事故。
为了顺应工程机械自动化、智能化的发展趋势[17],提高救援效率,本文对道路清障车的自动扶正控制进行了研究。根据事故车辆与道路清障车的几何位置关系,建立了扶正控制模型,获得了控制对象的变化规律,并分别利用常规PID控制算法和变参数PID(VAPID)控制算法,对该模型进行了仿真研究。
1 扶正过程建模
为简化模型,将事故车辆以长方体刚体代替,不考虑侧向位移,将扶正过程简化为定轴转动。模型采用四卷扬(主副卷扬各2个)。为保证扶正过程平稳,以扶正过程中事故车辆姿态为控制对象,研究扶正过程中各卷扬之间的位移关系。建立图1所示的扶正模型。图1中,AB为事故车辆高度;BC为事故车辆宽度;CD为事故车辆长度;AJ为事故车辆前悬长度;JK为事故车辆轴距;KF为事故车辆后悬长度;P、Q为道路清障车吊臂上主副卷扬固定滑轮位置;K、J、L、M为事故车辆轮胎钢圈位置;AOEF为事故车辆底盘。

图1 扶正模型
扶正时以4个轮胎钢圈作为捆扎固定位置。捆扎时,要求MN∥LR∥AB,NH∥RI∥OA,绳索PHM和PIL分别连接2个主卷扬,QK、QJ连接2个副卷扬。扶正过程中,设卷扬到吊钩的距离及LI、MH等长度保持不变,只有PH、PI、QK、QJ随事故车辆翻转角度而变化。
图2所示为扶正模型在YOZ平面的投影。设AB=a,BC=b,CD=c,AJ=d,AK=e,P点坐标为(x1,y1,z1),Q点坐标为(x2,y2,z2)。根据几何关系,可得


图2 扶正模型在YOZ平面投影图
扶正过程应安全平稳,避免二次事故,因此控制策略以事故车辆姿态平稳为首要考虑。假设事故车辆以角速度ω匀速扶正,即α=ωt。一旦确定ω及事故车辆特征参数、清障救援车辆与事故车辆的相对位置,根据上述公式即可求得扶正过程各卷扬位移变化曲线。
以一般的家用轿车为例,设事故车辆长宽高为4.8m、1.8m、1.4m,车辆前悬长度为 0.9m,后悬长度为1.2m,轴距为2.7m,即a=1.4m,b=1.8m,c=4.8m,d=0.9m,e=0.9+2.7=3.6m。道路清障车主副卷扬固定滑轮坐标为P(2m,-3m,4m)、Q(2m,-3.5m,3m),角速度ω=10°/min。将上述参数代入式(1)~式(4),可分别求得4个卷扬的位移曲线,如图3所示。

图3 卷扬位移曲线
扶正过程中,该位移曲线的变化量即为各卷扬收放绳索的长度,负值表示绳索收紧,正值表示卷扬放绳。因为扶正过程比较缓慢,以60s为间隔进行计算,将t+60时刻位移与t时刻位移相减,即可得到各卷扬工作时,位移随时间的变化曲线,如图4所示。

图4 卷扬位移变化曲线
2 液压回路AMESim建模
在AMESim环境下,根据道路清障车的实际起升回路[18],建立其扶正系统电液伺服模型,单个卷扬液压回路模型如图5所示。模型主要参数设定见表1。

图5 基于AMESim的道路清障车扶正系统仿真模型

表1 重要液压元件参数
3 AMESim与MATLAB联合仿真
工程实践中,经常采用常规PID控制。常规PID控制中,Kp、Ki、Kd根据对象模型或动态响应曲线进行整定[19]。变参数PID控制器将Kp、Ki、Kd取为偏差E的函数。根据偏差E的大小,实时改变这3个系数,加快对小偏差的反应,提高控制器对干扰的灵敏度,出现干扰时及时调节[20]。
VAPID控制算法的参数调整公式如下:
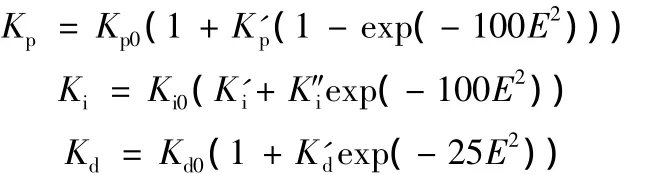

通过设置环境变量等,MATLAB可以实现与AMESim 的联合仿真[21]。在 MATLAB/Simulink环境中,分别搭建常规PID与VAPID控制系统。系统 Simulink模块见图 6、图 7,其中,AMESim Model模块为AMESim中经过系统编译、参数设置等生成供Simulink使用的S函数。图7中封装的VAPID模块内部组成如图8所示。
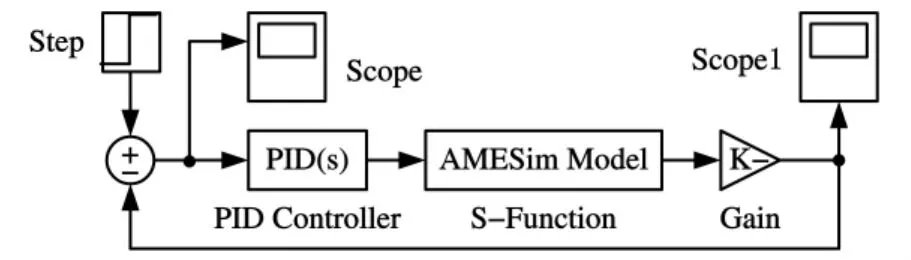
图6 常规PID控制系统Sim ulink模块图

图7 VAPID控制系统Sim ulink模块图

图8 VAPID Sim ulink模块图
常规PID与VAPID阶跃响应曲线如图9所示。将输入信号由阶跃信号改为4个卷扬实际位移变化曲线,仿真得到的跟踪误差见图10。
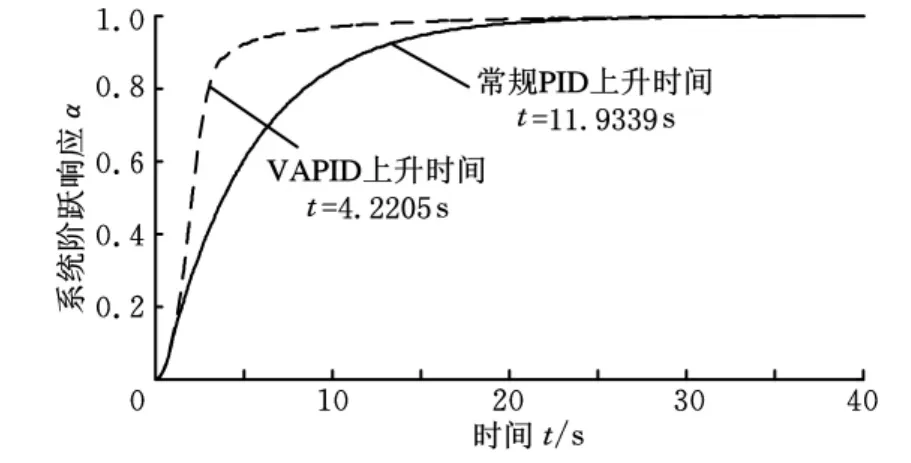
图9 阶跃响应曲线

图10 位移跟踪误差


图11 系统误差E2(t)曲线

图12 系统误差E2(t)的积分
由阶跃响应曲线及跟踪误差曲线可知:
(1)从仿真结果来看,常规PID也可以实现系统的稳定,但是利用VAPID控制,不仅能保证系统稳定,而且能使系统的阶跃响应更快,到达稳态的时间更短,基本无超调。
(2)在跟踪道路清障车各卷扬位移时,VAPID控制的系统跟踪误差比常规PID控制的系统跟踪误差衰减更快,且系统误差无回调现象,可以实现事故车辆的平稳扶正。
(3)在仿真过程中,VAPID控制比常规PID控制增加了3个参数,但设置并不复杂,能够使得控制效果提升明显。
4 结论
(1)建立了道路清障车扶正模型。通过扶正模型,只需确定事故车辆前悬长度、后悬长度、轴距及清障救援车作业位置等参数,即可获得控制对象的变化规律。(2)利用AMESim软件建立了道路清障车扶正系统的液压回路模型,分别采用VAPID与常规 PID算法进行了扶正控制,在MATLAB/Simulink环境中进行了仿真分析。仿真结果表明,VAPID相对于常规PID控制算法,在跟踪各卷扬实际位移时,误差衰减更快,且基本无超调现象出现,可以实现事故车辆的自动平稳快速扶正。研究结果为增强道路清障救援行业自动化水平、提高救援效率奠定了理论研究基础。(3)在实际情况中,车辆外形各式各样,事故对车辆外形的影响也不尽相同,本文将车辆侧翻后理想化为长方体刚体只是其中较为典型的事故形态。对于其他如混凝土车等车辆的扶正,需要根据实际情况进行建模和理论分析。
[1]张占国.重型清障车吊臂和托架强度刚度的有限元分析研究[D].长春:吉林大学,2005.
[2]张占国,周金来.重型清障车吊臂结构模态有限元分析[J].工程机械,2007,38(12):34-39.
Zhang Zhanguo,Zhou Jinlai.Finite Element Analysis in Boom Structural Mode of Heavy Barrier-clearing Vehicle[J].Construction Machinery and Equipment,2007,38(12):34-39.
[3]张占国,于畔光.拖吊分离型清障车拖架有限元模态分析[J].北华大学学报(自然科学版),2010,11(5):449-452.
Zhang Zhanguo,Yu Panguang.Finite Element Modal Analysis for Bracket of the Bracing-hoisting Separated Barrier- clearing Vehicle[J].Journal of Beihua University(Natural Science),2010,11(5):449-452.
[4]王书贤.汽车交通事故模式分析与救援车辆的研究开发[D].武汉:武汉理工大学,2007.
[5]乐韵斐,施俊俊,王临春.可折叠式道路清障车的机构设计及优化[J].现代制造工程,2010(3):115-118.
Le Yunfei,Shi Junjun,Wang Linchun.Mechanism Design and Optimization of the Road FoldableWrecker[J].Modern Manufacturing Engineering,2010(3):115-118.
[6]汤辛华.清障车:一种经济实用的操纵机构[J].商用汽车,2008(1):102-103.
Tang Xinhua.Introduction of Several Operating Methods of Hydraulic Pressure Systems of Wrecker[J].Commercial Vehicle,2008(1):102-103.
[7]汤辛华.道路清障车感应式随动托举装置[J].专用汽车,2006(5):13-14.
Tang Xinhua.Induced Servo Lift- up Equipment of Wrecker[J].Special Purpose Vehicle,2006(5):13-14.
[8]于睿坤,李万莉,周奇才.工程起重机伸缩臂控制回路动态模型与仿真[J].中国机械工程,2006,17(23):2457-2460.
Yu Ruikun,LiWanli,Zhou Qicai.Dynamic Model and Simulation of Crane Telescopic Boom Control Circuit[J].China Mechanical Engineering,2006,17(23):2457-2460.
[9]王宜华.现代大型液压起重机起升性能研究[D].大连:大连理工大学,2006.
[10]安振伟.中小型液压起重机起升系统仿真研究[D].长春:吉林大学,2008.
[11]张启君.清障车市场情况及发展简析[J].商用汽车,2007(1):85-87.
Zhang Qijun.Analysis of the Road- block Removal Truck Market and Its Development[J].Commercial Vehicle,2007(1):85-87.
[12]李忠生.国内清障车的技术现状及发展趋势[J].商用汽车,2003(11):50-51.
Li Zhongsheng.Domestic Technical Status and Developing Trend of Wrecker[J].Commercial Vehicle,2003(11):50-51.
[13]宁文祥.国外清障车救援实例展示[J].专用汽车,2010(3):35-36.
Ning Wenxiang.Foreign Wrecker Rescue Examples Show[J].Special Purpose Vehilce,2010(3):35-36.
[14]Olsen R.Teamwork Can Save Lives[J].On Call 24/7,2008,4(1):12.
[15]Luciano T.A Steep Challenge[J].On Call 24/7,2008,4(2):21-23.
[16]Luciano T.Different Conditions May Require You to“Think Out of the Box”[J].On Call 24/7,2008,4(3):6-8.
[17]王庆丰,魏建华,吴根茂,等.工程机械液压控制技术的研究进展与展望[J].机械工程学报,2003,39(12):51-56.
Wang Qingfeng,Wei Jianhua,Wu Maogen,et al.Progress and Prospects in the Research of Hydraulic Control for Construction Machinery[J].Chinese Journal of Mechanical Engineering,2003,39(12):51-56.
[18]沈全兴.液压传动与控制[M].北京:国防工业出版社,2010.
[19]Rovira A A,Murrill P W,Smith C L.Tuning Controllers for Set- point Changes[J].Instruments and Control Systems,1969,42(12):67-76.
[20]钟庆昌,谢剑英,李辉.变参数PID控制器[J].信息与控制,1999(8):273-277.
Zhong Qingchang,Xie Jianying,Li Hui. PID Controller with Variable Arguments[J].Information and Control,1998(8):273-277.
[21]陈娟娟.基于AMESim的静液传动车辆驱动系统控制及仿真[D].哈尔滨:哈尔滨工业大学,2010.
[22]Slotine J- JE,LiWeiping.Applied Nonlinear Control[M].Upper Saddle River,New Jersey,USA:Prentice Hall,1991.
[23]闵颖颖,刘允刚.Barbalat引理及其在系统稳定性分析中的应用[J].山东大学学报(工学版),2007,37(1):51-55.
Min Yingying,Liu Yungang.Barbalat Lemma and Its Application in Analysis of System Stability[J].Journal of Shandong University (Engineering Science),2007,37(1):51-55.

