立式捏合机搅拌桨曲面的NURBS表示与误差分析

展俊德 李锡文 史铁林

华中科技大学，武汉，430074

0 引言

立式捏合机作为固体推进剂研制和生产的关键设备，是固体推进剂技术的重要组成部分。两桨立式捏合机具有物料混合均匀、生产率高等优点，在固体推进剂的生产中得到了广泛的应用［1］。立式捏合机的混合效率及混合效果在很大程度上取决于搅拌桨的几何形状，故搅拌桨曲面设计是立式捏合机设计和制造过程中的一个重要环节［2］。两桨立式捏合机搅拌桨由实心桨与空心桨组成，搅拌桨曲面是由其水平截面轮廓线按照一定数值的螺旋升角顺时针或逆时针扫掠生成的。搅拌桨水平截面轮廓线是由自由曲线、圆弧和直线段等以一定的几何连续条件依次组合而成的复杂曲线，搅拌桨水平截面轮廓线和搅拌桨曲面不能用初等解析函数来表示。

非均匀有理B样条（NURBS）能够实现二次解析几何和自由曲线曲面的统一，通过局部改变控制点或权因子即可调整局部的曲线曲面形状，而不影响其他部分，具有良好的几何性质［3］。因此，本文根据搅拌桨不同高度的截面轮廓线生成了若干个3次NURBS平面曲线，利用蒙皮法生成了立式捏合机搅拌桨的NURBS曲面；在生成的NURBS曲面误差分析的基础上，提出了一种新的控制顶点投影法计算曲面理论坐标点到NURBS曲面的最小距离的算法，用以评价NURBS曲面的重构精度。

1 NURBS曲线曲面表示

一条k次NURBS曲线可以表示为一分段有理多项式矢函数［4］：

其中，ωi为权因子，分别与控制顶点Pi相关。首末权因子ω0＞0，ωn＞0，其余ωi≥0。Ni，k（u）是节点矢量U＝ （u0，u1，…，un＋k＋1）决定的k次规范B样条基函数，满足德布尔－考克斯递推公式：

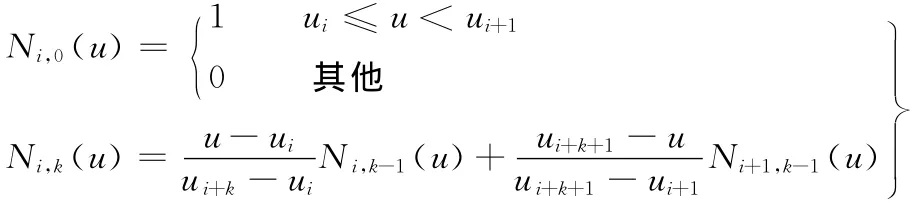
在实际应用中，节点矢量首尾的重复度取为k＋1次，即u0＝u1＝ … ＝uk＝0，un＋1＝un＋2＝…＝un＋k＋1＝1。这样使得曲线具有同次有理Bezier曲线的端点几何性质，即在权因子ω1，ωn－1≠0的情况下，曲线在首末端点处分别与控制多边形首末边相切。

类似于NURBS曲线，一张p×q次的NURBS曲面可表示为

其中，Pi，j呈矩形阵列，形成一个控制网格；ωi，j是与控制顶点Pi，j有关的权因子，规定四角控制顶点处的权因子ω0，0，ωm，0，ω0，n，ωm，n都大于0，其余ωi，j≥0，且顺序p×q个权因子不同时为0；Ni，p（u）和Nj，q（v）分别为沿u向的p次和沿v向的q次规范B样条基函数，同样由德布尔－考克斯递推公式确定；节点矢量U、V与NURBS曲线节点矢量的定义形式相同，这样可使曲面角点具有Bezier曲面的角点性质。

2 立式捏合机搅拌桨曲面的NURBS表示

2.1 立式捏合机搅拌桨的几何特征

立式捏合机两个搅拌桨（实心桨和空心桨）均垂直安装，其支撑轴位于桨叶的上部，两搅拌桨轴线均偏离混合釜中心轴线一定距离，即具有一定的偏心距。其中，实心桨的偏心距es小于空心桨的偏心距ek。两搅拌桨中心距为L，实心桨和空心桨直径为d，基圆直径为db，桨叶高度为h，混合釜直径为D。搅拌桨叶刀尖与混合釜内壁的最小间隙为c1，两搅拌桨叶之间的最小间隙为c2，桨叶底端与混合釜内底部之间的最小间隙为c3。在物料混合过程中，两搅拌桨在混合釜内做行星捏合运动，实心桨和空心桨的自转角速度分别为ωs和ωk，公转角速度均为ωH。为了使物料在混合釜内自上而下、自下而上充分翻动混合，搅拌桨叶表面采用螺旋曲面，根据捏合原理，空心桨和实心桨螺旋角方向应该相反，根据两个桨叶的转速比，螺旋角也应满足一定的比例关系。立式捏合机搅拌桨外形及主要几何尺寸如图1所示。

2.2 立式捏合机搅拌桨的NURBS表示

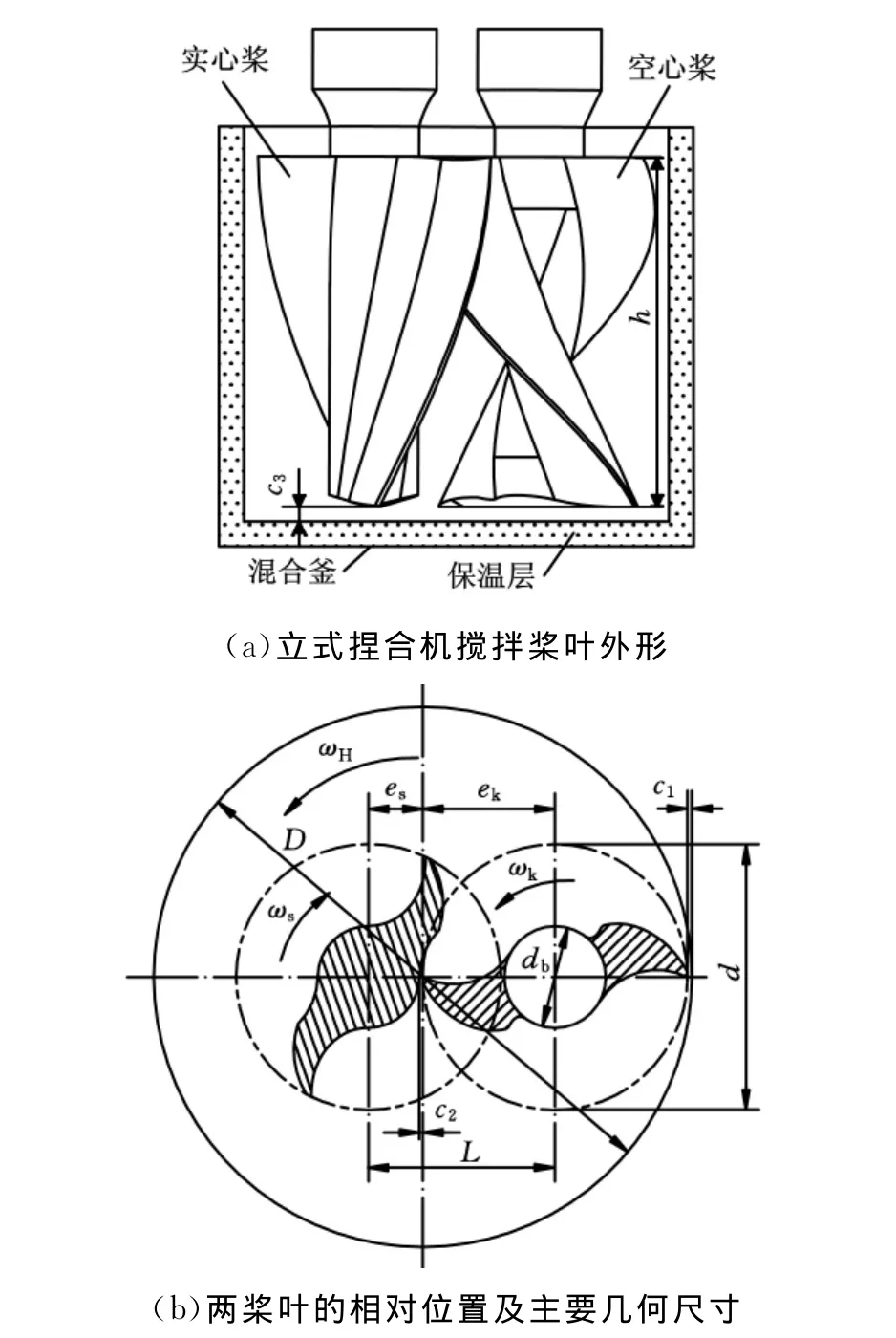
图1 立式捏合机工作原理

立式捏合机搅拌桨曲面的NURBS表示过程是：首先根据搅拌桨水平截面轮廓线上的理论型值点，利用参数曲线方法反算出控制顶点，同理可以求出桨叶不同高度水平截面轮廓线的控制顶点，进而利用蒙皮法反求出桨叶曲面的控制顶点，再用参数曲面方法构造出曲面模型，最后在Visual C＋＋6.0编程环境下，调用 OpenGL 接口函数，生成搅拌桨水平截面轮廓的NURBS曲线和搅拌桨的NURBS曲面。具体构造过程如下［5－7］：

（1）根据搅拌桨水平截面轮廓线上的型值点，依次生成各曲线段（自由曲线、圆弧段、直线段等）的NURBS表示；把阶次小于3次的NURBS曲线段升阶为3次；依次拾取各曲线段的控制顶点和权因子，相邻两段的控制顶点和权因子要满足连接点处的几何连续性要求，确定复合后整条曲线的控制顶点和权因子；计算各曲线段的控制多边形长度在复合曲线的控制多边形总长中所占有的比例，得出各曲线段在整体节点域u∈［0，1］中的定义区间，依次对各曲线段的节点做整体参数变换，得到复合曲线在整体参数下的节点矢量。得出的立式捏合机搅拌桨水平截面轮廓线的3次NURBS曲线如图2所示。图2中左半部分是实心桨的水平截面曲线，右半部分是空心桨中部的水平截面曲线。

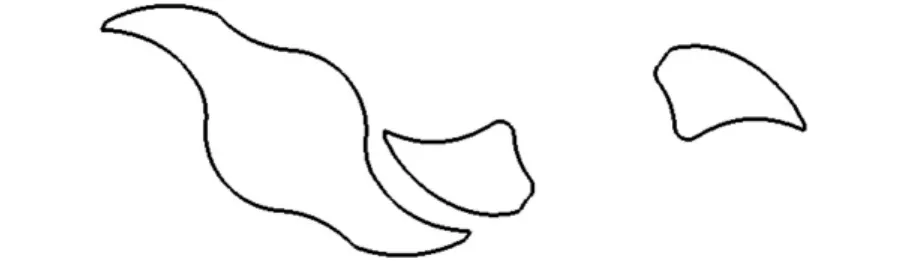
图2 立式捏合机搅拌桨截面轮廓的NURBS表示

（2）由于搅拌桨曲面是由其水平截面轮廓线以一定的螺旋升角顺时针或逆时针扫掠生成的，所以在搅拌桨不同轴向位置处的水平截面曲线形状是相同的，只是在其径向平面内绕轴向做了不同角度的旋转。所以，在求出空心桨和实心桨某一个水平位置截面轮廓线的NURBS表示的基础上，依据NURBS曲线的几何不变性，可以求出桨叶若干个不同高度水平截面轮廓线的NURBS表示。

（3）在复杂曲面的外形设计中，曲面多是由一组给定的截面曲线蒙皮生成的。由于不同高度搅拌桨截面轮廓的NURBS曲线的节点和阶次相同，不需要进行截面曲线间的u向相容处理，只需计算相邻截面NURBS曲线的对应控制顶点之间的距离，故采用累积弦长参数法计算v向节点矢量。以各截面曲线的NURBS控制顶点为型值点反算出NURBS曲面的控制顶点。对于空心桨，由于上下实心部分曲面与中间空心曲面的交线满足文献［8］提出的条件，故在曲面拼接处至少是G1连续的。利用蒙皮法生成的立式捏合机搅拌桨的NURBS曲面如图3所示。

图3 立式捏合机搅拌桨曲面的NURBS表示

3 曲面误差分析

为了验证所生成的NURBS曲面的精确性，本文以计算得到的曲面理论坐标点到NURBS曲面的最小距离作为评价NURBS曲面的误差值［9］。最小距离越小，说明生成的NURBS曲面精度越高。关于点到NURBS曲面的投影和距离的算法，国外相关学者已经做了很多研究［10－14］。通常地，计算一点P到曲面S（u，v）的最小距离通常可以转化为计算点在曲面上的投影［15］，即要满足：

由于点P在曲面S（u，v）上可能不存在或存在若干个投影点，即式（3）可能无解或存在若干个解，为此，本文提出了一种新的利用控制顶点投影法计算点到NURBS曲面最小距离的算法。该算法首先将控制顶点投影到NURBS曲面上，得到相应的投影点；其次在NURBS曲面上依次生成相邻投影点之间的曲线，这些曲线将NURBS曲面分割成若干个至少是G1连续的曲面片，使得点P在每个曲面片上至多存在一个投影点；最后通过判断点P与每个曲面片边界曲线之间的关系，可以得出点P在曲面片上是否存在投影点，计算点P与投影点（如果存在）之间的距离，即为点P到该曲面片的最小距离；同理可以求出点P到其他曲面片的最小距离，这些最小距离中的最小值即为点P到整个NURBS曲面的最小距离。下面给出该算法的具体实现步骤。

3.1 将控制顶点投影到NURBS曲面上

依次将每行控制顶点向NURBS曲面进行投影，得出对应的投影点。以控制顶点Pi，j为例，Pi，j在曲面上的投影点Pti，j应该满足式（3），即控制顶点Pi，j与其在曲面上的投影点Pti，j的线段分别和投影点Pti，j的u向、v向切矢之间的点积为0。特别地，对于第一行和最后一行的u向控制顶点，投影到对应的NURBS曲面u向边界曲线上，仅要求控制顶点与投影点的线段和投影点的u向切矢之间的点积为0；同样地，对于第一列与最后一列的v向控制顶点，也投影到对应的NURBS曲面v向边界曲线上，仅要求控制顶点与投影点的线段和投影点的v向切矢之间的点积为0；如果控制顶点在NURBS曲面上，则该控制顶点与投影点重合；如果曲面上存在u向或v向G0连续的折痕曲线时，在折痕曲线两侧，找出一个距离折痕曲线最近的控制顶点，将该控制顶点投影到折痕曲线上，仅要求该控制顶点与投影点的线段与投影点的v向或u向切矢之间的点积为0。

在求投影点的计算过程中，目前一般利用Newton－Raphson迭代方法对式（3）进行求解，此方法计算速度快，可以达到较高的计算精度，迭代公式为

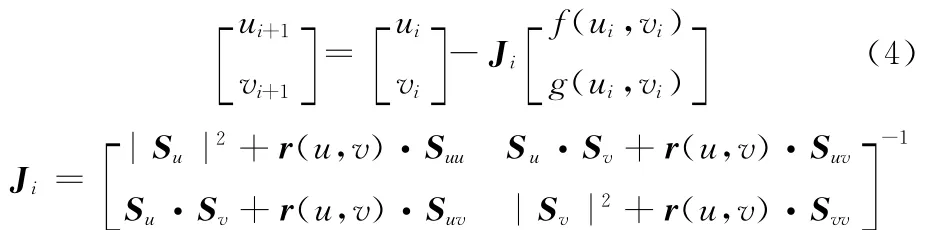
假定上一个控制顶点Pi，j－1在曲面上的投影点Pti，j－1对 应 的 节 点 值 为 （uti，j－1，vti，j－1），以（uti，j－1，vti，j－1）作为迭代初始值，其收敛准则为

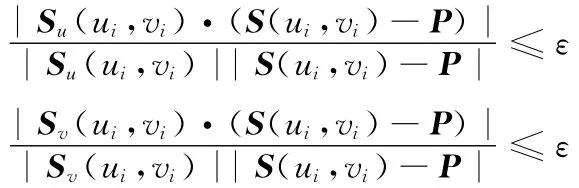
ε为计算精度，这里ε取1×10－10，求出控制顶点Pi，j在NURBS曲面上的投影点对应的节点值（uti，j，vti，j），再利用式（2）求出Pi，j在曲面上的投影点Pti，j。类似地可以求出其他控制顶点在NURBS曲面上的投影点以及投影点对应的节点值。

3.2 NURBS曲面片的生成

由于在曲面尖点、角点等只满足G0连续的位置处有一个或多个控制顶点投影点，故在u向或v向折痕曲线上也有多个控制顶点的投影点。这样，u向或v向相邻投影点之间至少满足G1连续。以控制顶点Pi，j、Pi＋1，j、Pi，j＋1和Pi＋1，j＋1在 NURBS曲面对应的投影点Pti，j、Pti＋1，j、Pti，j＋1和Pti＋1，j＋1为例，投 影 点 对 应 的 节 点 值 分 别 为 （uti，j，vti，j）、（uti＋1，j，vti＋1，j）、 （uti，j＋1，vti，j＋1） 和 （uti＋1，j＋1，vti＋1，j＋1），当 节 点 变 量 （u，v）在 （uti，j，vti，j）与（uti＋1，j，vti＋1，j）之间以微小量（Δu，Δv）变化时，可以得到投影点Pti，j与Pti＋1，j之间在 NURBS曲面上的连续曲线，由多元函数的微分公式知，这些曲线至少是G1连续的。类似地可以得到其他相邻投影点之间在NURBS曲面上的曲线。这些曲线把NURBS曲面分割成若干个至少是G1连续的曲面片，而曲面上尖点、角点或折痕曲线等G0连续的位置被分割在曲面片的边界曲线上。

图4形象化地说明了控制顶点投影点间的曲线将NURBS曲面分割成若干个曲面片的实现过程。

图4 控制顶点投影法分割NURBS曲面

3.3 计算点P到每个曲面片的最小距离

对 于 曲 面 片Pti，jPti＋1，jPti，j＋1Pti＋1，j＋1， 由NURBS曲面的凸包性质及曲面片边界曲线的变差缩减性质可知，曲面片内在u向或v向上至多存在一条极值点曲线。由于曲面片内的Su和Sv是连续的，所以曲面片的Su和Sv变化边界值在曲面片的四条边线上，又由于边线也是连续的，所以曲面片的Su和Sv边界值在曲面片的四个角点Pti，j、Pti＋1，j、Pti，j＋1和Pti＋1，j＋1处。将曲面片四个角点的Su和Sv分别投影到XY平面、XZ平面和YZ平面，得出四个角点的Su和Sv二维投影向量，依据连续函数极值存在的判别条件，可以点积四个角点Pti，j与Pti＋1，j、Pti，j＋1与Pti＋1，j＋1的Su，Pti，j与Pti，j＋1、Pti＋1，j与Pti＋1，j＋1的Sv在三个投影面上的向量，如果点积值均是正，说明曲面片的Su或Sv是单调连续的；如果存在负值，说明曲面片内存在u向或v向的极值曲线，则利用二分法可以在相应边线上找出极值点，在曲面片上连接极值点，极值点间的曲线将曲面片分为两片u向或v向单调连续的小曲面片。类似地，可以使得其他曲面片在u向和v向上是单调连续的。

由于曲 面 片Pti，jPti＋1，jPti，j＋1Pti＋1，j＋1或 其 子曲面片在u向和v向上是单调连续的，则在曲面片上f（u，v）与g（u，v）是连续函数，可以通过计算f（u，v）与g（u，v）在曲面片四个角点的值，判断点P在曲面片内的投影点Pt是否存在。具体过程如下：

f（u，v）如果在Pti，j与Pti＋1，j的值异号，或在Pti，j＋1与Pti＋1，j＋1的值异号，说明点P在曲面片上的u向投影存在；如果都是同号，说明点P在曲面片上的u向投影不存在。同样地，g（u，v）如果在Pti，j与Pti，j＋1的值异号，或在Pti＋1，j与Pti＋1，j＋1的值异号，说明点P在曲面片上的v向投影存在；如果都是同号，说明点P在曲面片上的v向投影不存在。

如果点P在曲面片上的u向投影和v向投影同时存在，说明点P在曲面片上的投影点存在；如果点P在曲面片上的u向投影和v向投影同时不存在，说明点P在曲面片上的投影点不存在。

如果投影点存在，则点P到曲面片的最小距离就是点P与其投影点Pt之间的距离。如果投影点不存在，则点P到曲面片的最小距离点存在于曲面的四个边线上。如果仅u向投影存在，则在相应的曲线段Pti，jPti＋1，j或Pti，j＋1Pti＋1，j＋1上利用二分法求出u向投影点；同样地，如果仅v向投影存在，则在相应的曲线段Pti，jPti，j＋1或Pti＋1，jPti＋1，j＋1上利用二分法求出v向投影点；点P到曲面片的最小距离就是点P与u向投影点或v向投影点之间的距离。如果u向投影和v向投影都不存在，计算点P与曲面片四个角点之间的距离，其中最小值就是点P到曲面片的最小距离。

在投影点的计算上，以曲面片一个角点作为初始值，利用Newton－Raphson迭代方法求解式（3）。由于曲面片至少是G1连续的，在u向和v向是单调连续的，u向边界曲线间Su变化不大，v向边界曲线间Sv变化也不大，所以，以曲面片的角点为初始值，一般都可以使迭代过程收敛。

3.4 计算点P到NURBS曲面的最小距离

比较点P到各曲面片的最小值，找出全局最小值，即为点P到整个NURBS曲面的最小距离。取多组搅拌桨水平截面轮廓线上的理论坐标点，利用控制顶点投影法计算理论点到搅拌桨NURBS曲面的最小距离，得出的最大距离为0.1mm，说明立式捏合机搅拌桨的NURBS曲面精度是较高的。

4 结语

本文在立式捏合机搅拌桨水平截面曲线的NURBS表示的基础上，利用蒙皮曲面方法，生成了立式捏合机搅拌桨的NURBS曲面。在此基础上，提出了一种新的控制顶点投影法计算点到NURBS曲面最小距离的方法，验证了立式捏合机搅拌桨曲面的NURBS表示的精确性和可靠性，为搅拌桨的优化设计打下了较好的基础。同时，控制顶点投影法计算点到NURBS曲面最小距离的算法具有重要的实用价值，可以在CAD/CAM等领域内进行进一步推广和应用。

［1］叶定友，张德雄.中国航天固体火箭推进技术的发展［J］.中国航天，2002（12）：24－27.

Ye Dingyou，Zhang Dexiong.Evolution of Chinese Aerospace Solid Rocket Propulsion Technology［J］.Aerospace China，2002（12）：24－27.

［2］王正方，翟瑞清.立式捏合机搅拌桨的设计［J］.固体火箭技术，1993（1）：65－69.

Wang Zhengfang，Zhai Ruiqing.The design of Stirring Blades of Vertical Kneading Machine and Parametric Calculations［J］.Journal of Solid Rocket Technology，1993（1）：65－69.

［3］朱心雄.自由曲线曲面造型技术［M］.北京：科学出版社，2000.

［4］施法中.计算机辅助几何设计与非均匀有理B样条（CAGD ＆ NURBS）［M］.北京：高等教育出版社，2001.

［5］张乐年，周来水，周儒荣.基于复杂曲线的NURBS蒙皮曲面［J］.工程图学学报，1996，17（2）：58－63.

Zhang Lenian，Zhou Laishui，Zhou Rurong.Research in Nurbs Skinning Surface Based on Complex Curve［J］.Journal of Engineering Graphics，1996，17（2）：58－63.

［6］Piegl L A，Tiller W.Algorithm for Approximate NURBS Skinning［J］.Computer－aided Design，1996，28（9）：699－706.

［7］Yoshimasa T.Skinning－Surface Generation Based on Spine－Curve Control［J］.The Visual Computer，2000，16（2）：134－140.

［8］于丕强，施锡泉.双三次NURBS曲面的G1连续性条件［J］.大连理工大学学报，2004，44（3）：330－333.

Yu Piqiang，Shi Xiquan.G1Continuous Conditions for Bicubic NURBS Surfaces［J］.Journal of Dalian University of Technology，2004，44（3）：330－333.

［9］柯映林，李齐敏.基于截面轮廓的NURBS曲面重建［J］.中国机械工程，2005，16（12）：1083－1087.

Ke Yinglin，Li Qimin.Reconstruction of NURBS Surface from Spatial Cross－sections［J］.China Mechanical Engineering，2005，16（12）：1083－1087.

［10］DyllongE，Luther W.Distance Calculation Between a Point and a NURBS Surface［C］//4th International Conference on Curves and Surfaces.Saint－Malo，1999：55－62.

［11］Piegl L A，Tiller W.Parameterization for Surface Fitting in Reverse Engineering［J］.Computer－aided Design，2001，33（8）：593－603.

［12］Ma Y L，Hewitt W T.Point Inversion and Projection for NURBS Curve and Surface：Control Polygon Approach［J］.Computer－aided Geometric Design，2003，20（2）：79－99.

［13］Selimovic I.Improved Algorithms for the Projection of Points on NURBS Curves and Surfaces［J］.Computer Aided Geometric Design，2006，23（2）：439－445.

［14］PieglL A，Rajab K，Smarodzinava V，et al.Point－Distance Computations：A Knowledge－Guided Approach［J］.Computer－aided Design and Applications，2008，5（6）：855－866.

［15］Zhou J，Sherbrooke E C，Patrikalakis N M.Computation of Stationary Points of Distance Functions［J］.Engineering with Computers，1993，9（4）：231－246.