表面形貌测量数据处理算法研究

王移风 曹衍龙 徐 朋 金 鹭 杨将新

1.浙江科技学院，杭州，310023 2.浙江理工大学，杭州，310018 3.浙江大学，杭州，310027

0 引言

随着机械加工精度的不断提高，与表面形貌有关的应用也越来越广泛，表面形貌测量技术在精密加工行业和各类研究领域中的地位显得愈发重要。白光谱线扫描干涉法是表面形貌检测的有效方法，适合于大范围、高精度的测量，但由于图像数据量大，数据处理时间过长，限制了在实时测量中的应用。如何加速数据处理的过程，缩短数据处理时间，提升系统整体的实时性已成为关键问题。

图形处理器GPU可以在较低的成本下，以较快的速度完成科学计算中的并行处理问题，并具有十分明显的加速效果，近年来图形处理器已在诸如光学测量［1］、物理模拟［2－4］、科学计算［5－6］、图像处理［7－10］等领域得到成功应用。

本文介绍一种利用GPU进行数据处理的实时表面形貌测量方法，利用NVIDIA Geforce GTS250图形卡（16个流多处理器，1100MHz）进行数据处理，对比分析了CPU运行下的串行处理算法的运行时间和精度，实验表明基于GPU的数据处理可以得到很好的效果。

1 系统结构

所搭建的表面形貌测量系统主要由白光谱线扫描干涉模块、声光滤光器控制模块、图像采集模块和数据处理模块组成。其系统结构如图1所示。白光源经过透镜发出平行光，经过滤光装置后成为波长呈线性变化的单色光。这束单色光进入类似迈克尔逊干涉仪的系统之中，经过分光镜BS后分为两束，一束打在参考反射镜上，另一束打在被测工件的表面。两束光反射后，重新在分光镜BS处汇聚并产生干涉条纹。干涉图像由CCD采集并存放到计算机中进行处理。

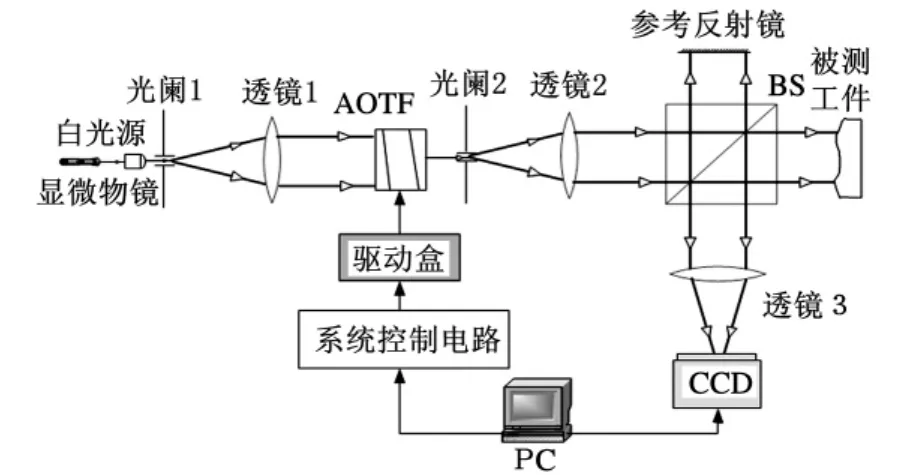
图1 系统结构

干涉图像上单个像素点的灰度值表征了某一波长下该点发生干涉时其干涉条纹的光强信息。由CCD上某像素点 （x，y）探测到的光强可表示为

式中，I1（σ）、I2（σ）分别为由被测工件与参考反射镜反射回来的光线光强；σ为波数；φ（x，y，σ）为干涉信号的相位；h（x，y）为该点处两束反射光的绝对光程差。

由波数改变而引起的相位改变为

可得点（x，y）的绝对光程差h（x，y）为

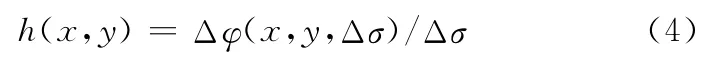
滤光装置可以使得波数呈线性变化，同时CCD的采集过程也是线性的，因此通过求取波数变化Δσ时的相位变化Δφ（x，y，k），就能求得该点的绝对光程差。通过分析整张干涉图像上所有像素点的相位变化得到绝对光程差，以此能描绘出该被测区域表面的形貌特征，以进行下一步的分析和评定，由此可见精确的相位是获得绝对光程差的关键。

本文采用快速傅里叶变换法［11-12］来对光强分布函数进行分析，此时式（1）可改写为

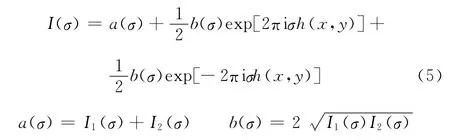
a（σ）和b（σ）相对于光程差h（x，y）来说是缓变元，其频率远低于后者，故可以在频域上对低频部分进行滤波，将a（σ）滤去。对式（5）做傅里叶变换：

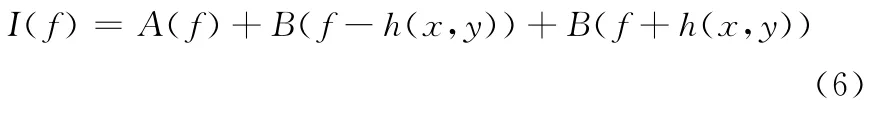
将a（σ）过滤之后做反傅里叶变换，并通过对数运算分离相位信息：

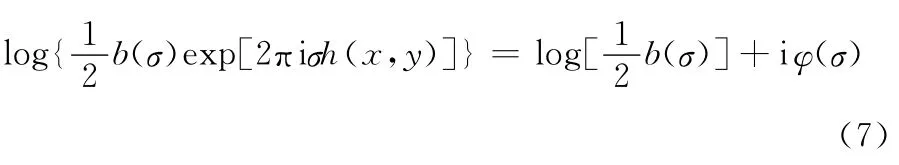
式（7）中的虚数部分即为每个波数所对应的相位值。此时的相位值是以2π为周期分布的，并不能直接应用，需要先进行相位的展开运算，通过展开的相位值可以求解该点的绝对光程差。

2 基于GPU的数据处理算法

鉴于上述算法在处理干涉图像时，是对干涉图上的各像素点光强进行分析，而每个像素点之间的处理是相互独立的，故可以采用并行处理的方式对这一过程进行加速。

2.1 统一计算设备架构CUDA［12］

在CUDA架构中，CPU作为主机执行一些复杂的逻辑处理和事务处理，同时作为协处理器的设备端GPU负责执行高度线程化的并行处理任务。CUDA程序就是由主机端的串行执行部分加上设备端并行执行的一系列内核函数组成的。内核函数通过一个线程网格（Grid）来执行。执行内核函数的线程网格包含着两层并行的结构，即线程块（Block）和线程（Thread），线程块之间以及每个线程块中的所有线程之间都是相互独立并可以并行执行程序的。本文的并行处理算法就是通过构建一系列内核函数实现的。

2.2 基于CUDA的GPU并行算法的设计

傅里叶变换分析法的GPU并行实现流程如图2所示。首先，在内存中完成初始化；其次，拷贝到显存运用FFT－IFFT方法滤除多余的光强信号并提取光强分布函数的相位信息；最后，通过求解相位跳变并展开干涉信号相位求取绝对光程差。

图2 傅里叶变换分析法的GPU并行实现流程图

（1）对光强分布函数进行快速傅里叶变换。首先将原始干涉信号进行快速傅里叶变换。

（2）带通滤波。设计内核函数进行带通滤波将式（5）中的变元a（σ）过滤掉。过滤前后的频率分布如图3所示。

（3）傅里叶反变换。滤去a（σ）之后，利用CUDA做傅里叶反变换，将信号从频域转换到时域上，此时存在归一化问题，即傅里叶反变换后的值应除以上步FFT的点数才是其真实值。

（4）求取相位信息。将过滤a（σ）后的信号做对数运算，得到结果的虚数部分即为相位值。这一过程对于每一个波数σ都是独立的，故可以选择大尺度的线程块维度。

（5）求取相位跳变。由FFT－IFFT法求得的相位呈周期性分布，需对其进行相位展开。在展开之前先求取其相位跳变，分析其相位分布情况。

图3 过滤前后的幅值分布

（6）相位展开。相位展开原理如图4所示。其表达形式为

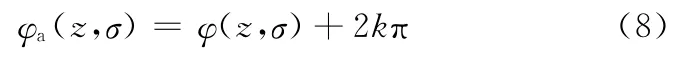
式中，k为相位周期数。

图4 相位展开原理

（7）求取绝对光程差。展开相位后，得到每个波数所对应的相位值，由最小二乘法拟合出相位分布，根据式（4）求取该像素点对应工件表面的绝对光程差。

3 实验结果分析

3.1 结果比较

基于GPU的相位计算并行处理算法与CPU运行下的CPU串行处理算法进行实验比较。

图5a、图5b所示为150像素×150像素区域CPU和GPU的运算结果；图5c为该块绝对光程差数据的相对误差，其定义为：相对误差＝（GPU结果－CPU结果）／CPU结果。

图5c表明，CPU和GPU运算结果相对误差最大仅为1.5×10－6，可以忽略不计。

3.2 加速对比

设计开发了基于GPU的相位计算并行处理算法，并与CPU运行下的CPU串行处理算法的运行时间进行实验比较，见表1。为对比不同数据量下的两种算法的运算效率，分别对多个不同大小范围的图像区域进行处理。处理分为相位求取阶段和相位展开求光程差阶段。

表1 傅里叶分析法GPU及CPU处理速度及加速比

由表1可以得出：GPU加速比随着数据处理数量的增多而增大。在数据量小的情况下内存和显存之间数据搬运的时间没有被GPU运算时间掩盖，使用CUDA进行小计算量的运算是不划算的，只有当并行计算在整个应用中所占的比例较大时，其加速性能才能很好地得到体现。

相位展开阶段的加速比大于相位求取阶段的加速比，这是由于相位展开阶段全部采用速度极快的共享存储器进行并行运算，并且在这个过程中并行算法避免了程序出现共享存储器区冲突问题。

4 结束语

本文基于CUDA提出了表面形貌测量的数据处理算法，经实验表明运算速度比传统的算法大幅提高，其运算精度也可以得到保证。基于GPU的数据处理算法对表面形貌实时测量有重要意义。

［1］Zhang S.GPU－assisted High－resolution，Realtime 3－D Shape Measurement［J］.Optics Express，2006，14（20）：9120－9130.

［2］Hu L，Xuan L，Li D，et al.Real－time Liquid－crystal Atmosphere Turbulence Simulator with Graphic Processing Unit［J］.Optics Express，2009，17（9）：7259－7269.

［3］Ren N，Liang J，Qu X，et al.GPU－based Monte Carlo Simulation for Light Propagation in Complex Heterogeneous Tissues［J］.Optics Express，2010，18（7）：6811－6824.

［4］Fang Q，Boas D A.Monte Carlo Simulation of Photon Migration in 3DTurbid Media Accelerated by Graphics Processing Units［J］.Optics Express，2009，17（22）：20178－20192.

［5］Kang H，YamaguchiT，Yoshikawa H，et al.Acceleration Method of Computing A Compensated Phase－added Stereogram on A Graphic Processing Unit［J］.Applied Optics，2008，47（31）：5784－5790.

［6］Bin H，Tarek T.Acceleration of Spiking Neural Network Based Pattern Recognition on NVIDIA Graphics Processors［J］.Applied Optics，2010，49（10）：B83－B91.

［7］Pan Y，Xu X，Solanki S，et al.Fast CGH Computation Using S－LUT on GPU［J］.Optics Express，2009，17（21）：18543－18556.

［8］Kang H，Yaras F，Onural L.Graphics Processing U－nit Accelerated Computation of Digital Holograms［J］.Appled Optics，2009，48（34）：H137－H144.

［9］Vinegoni C，Fexon L，Feruglio P F，et al.High Throughput Transmission Optical Projection Tomography Using Low Cost Graphics Processing Unit［J］.Optics Express，2009，17（25）：22320－22333.

［10］Shimobaba T，Sato Y，Miura J，et al.Real－time Digital Holographic Microscopy Using the Graphic Processing Unit［J］.Optics Express，2008，16（16）：11776－11782.

［11］Sandoz P，Tribillon G，Perrin H.High－resolution Profilometry by Using Phase Calculation Algorithms for Spectroscopic Analysis of White－light Interferograms［J］.Journal of Modern Optics，1996，43（4）：701－708.

［12］Kuwamura S，Yamaguchi I.Wavelength Scanning Profilometry for Real－time Surface Shape Measurement［J］.Applied Optics，1997，36：4473－4482.