素域Fp 上的3-李代数
白瑞蒲,李奇勇,王伟东,程荣
(河北大学 数学与计算机学院,河北 保定 071002)
1 预备知识
n-李代数在数学与数学物理的很多分支中都有应用[1-4].因为n-李代数是具有多元运算的非结合代数[5-8],其结构要比具有二元运算的李代数结构要复杂的多,而且构造有限维的多元李代数一直是多元李代数结构研究的首要课题.在文献[9]和[10]中,利用已知代数实现了3-李代数.利用特征大于零的域上的群代数,群代数上的线性函数构造的导子,及群代数的自同构实现特征大于零的域上的3-李代数.给出了一种新的构造3-李代的方法.首先介绍用到的根本概念参见文献[5].
定义1 n-李代数L 是域F 上具有n-元线性运算[,…,]的线性空间,且对任意x1,…,xn,y1,…,yn∈L 满足下列恒等式
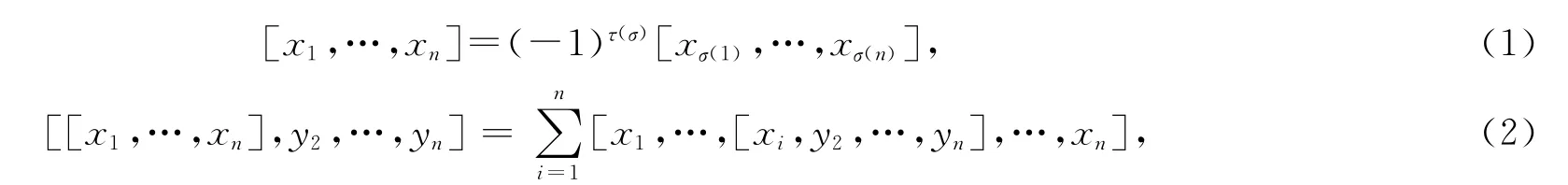
其中σ∈Sn,τ(σ)等于0或1,当σ是偶排列或奇排列时.
定义2 设L 是n-李代数,D:L→L 是线性映射,如果D 满足对任意x1,…,xn∈L,

则称D 为L 的导子.L 的导子全体记为Der(L),按照换位运算构成线性李代数.
定义3 设L 是n-李代数,ω:L→L 是线性映射,如果ω 满足对任意x1,…,xn∈L,
ω([x1,…,xn])=[ω(x1),…,ω(xn)],
则称ω 为L 的自同构.L 的自同构全体构成一个群,称为L 的自同构群,记为Aut(L).
2 主要结果
设Fp是特征为p 的素域,即具有运算
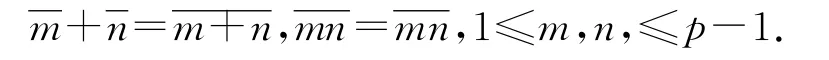
域Fp的加法群记为
设(A,+,·)是域Fp上以,1≤m≤p-1}为基的交换的结合代数,通常称为的群代数,
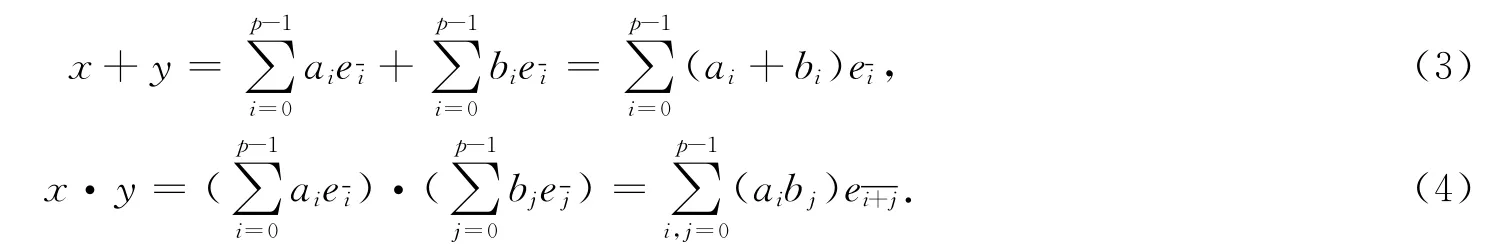
为简单起见,记x·y 为xy.

是交换结合代数A 的导子.
证明 由式(5)可知,α*是A 的线性映射.且对A 的任意2个基向量

所以α*是交换结合代数A 的导子.
引理2 设ω:A→A 按如下定义的映射

则ω 是交换结合代数A 的代数自同构,且ω 满足ω2=IdA.
证明 由式(3)可知,ω 是A 的线性映射.且对A 的任意2个基向量

引理3 如上定义的ω 及α*满足下列等式

证明 由式(5)和式(6)可知,对A 的任意基向量em∈A,
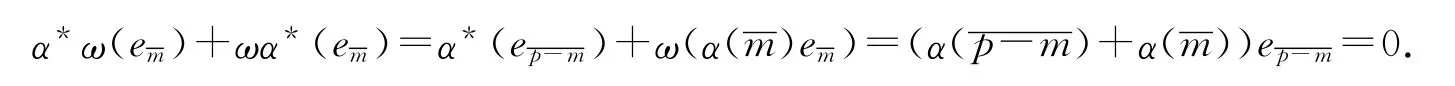
所以式(7)成立.
定理1 设(A,+,·)是域Fp上以为基的具有运算(3)和(4)的交换结合代数,α是任意一个加群同态,α*与ω 分别按等式(5)和(6)定义.则A 按下列运算构成3-李代数:对任意
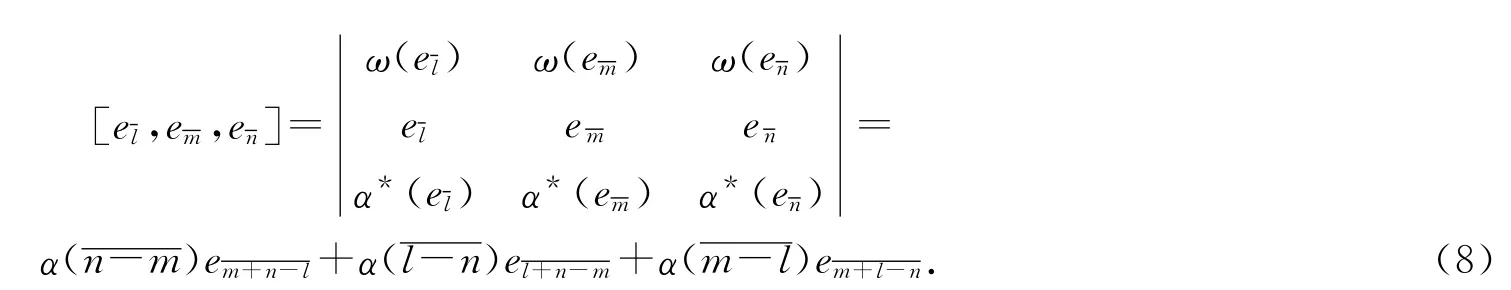
证明 显然,按式(8)定义的A 的3-元运算是具有交错性的3-元线性运算.且对任意A,因为

由上述讨论,直接计算可得

其中Γ(el,em,en)是el,em,en的循环和,

由以上证明可知,3-元运算(8)满足Jacobi等式.所以A 按运算(6)构成3-李代数.
由于Fp是特征为p 的素域,所以任意群同态α:F+p→F+p,α(m)=mα(1),记α(1)=a.则α(m)=m a.
推论1 设(A,+,·)是域Fp上以,1≤m≤p-1}为基的具有运算(3)和(4)的交换结合代数,则对任意则A 按下列运算构成3-李代数:对任意
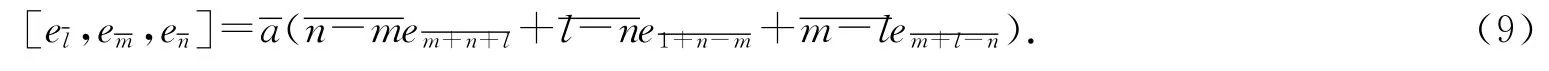
证明 结论可从定理5直接得到.
如果Fp=F3,则得F3上3-维3-李代数A 具有乘法表.
所以F3上的3-维3-李代数具有一维理想
[1] NAMBUY Y.Generalized Hamiltonian dynamics[J].Phys Rev D,1973(7):2405-2412.
[2] TAKHTAJANL.On foundation of the generalized Nambu mechanics[J].Comm Math Phys,1994(160):295-315.
[3] BAGGER J,LAMBERT N.Gauge symmetry and supersymmetry of multiple M2-branes[J].Phys Rev D,2008(77):065008.
[4] HO P,HOU R,MATSUO Y.Lie 3-algebra and multiple M2-branes[J].arXiv,2008:0804.2110.
[5] FILIPPOV V T.n-Lie algebras[J].Sib Mat Zh,1985(26):126-140.
[6] BAI Ruipu,WU Wanqing.Hypo-nilpotent ideals of n-Lie algebras[J].Journal of Natural Science of Heilongjiang University,2001,28(1):4-7.
[7] 白瑞蒲,肖文颖.4维3-lie代数的导子代数[J].河北大学学报:自然科学版,2008,28(3):228-230.BAI Ruipu,XIAO Wenying.Derivation algebras of 4-dimensional 3-Lie algebras[J].Journal of Hebei University:Natural Science Edition,2008,28(3):228-230.
[8] BAI Ruipu,SHEN Caihong,ZHANG Yaozhong.3-Lie algebras with an ideal N[J].Linear Alg Appl,2009,431:673-700.
[9] BAI Ruipu,BAI Chengming,WANG Jinxiu.Realizations of 3-Lie algebras[J].J Math Phys,2010(51):063505.
[10] 白瑞蒲,周恒,李佳倩.Y-矩阵构成的3-李代数的结构[J].河北大学学报:自然科学版,2012,32(5):449-452.BAI Ruipu,ZHOU Heng,LI Jiaqian.3-Lie algebras constructed byγ-matrices[J].Journal of Hebei University:Natural Science Edition,2012,32(5):449-452.

