汽车轮毂轴承单元带凸缘内圈的有限元分析

边起，雷良育，姚立健，刘绿朋，姜金为

(浙江农林大学 工程学院,浙江 临安 311300)

汽车轮毂轴承单元是汽车的关键零部件之一。它主要承受汽车整车重量，既承受径向和轴向载荷，又承受车辆在不同行驶工况下的复杂动载荷，并为轮毂的传动提供准确的向导[1]。轮毂轴承单元按照与汽车传动系统其他元件集成方式的不同可分为4代,目前应用较为广泛的是第3代轮毂轴承单元[2-3]。NSK开发的旋压成型第3代轮毂轴承单元去掉了锁紧螺母，不仅减小了轮毂轴承单元的质量和尺寸，还提高了车辆的可靠性[3]。对于轮毂轴承单元，不仅要具有轴承的功能，还需要保证结构的强度、刚度等基本性能指标[4-5]。为了发现和解决试验中难以发现的问题，缩短产品开发周期，降低成本，有限元分析技术已经成为非常必要的手段[6-7]。下文对轮毂轴承单元带凸缘内圈进行有限元分析，研究其唇边的受力情况及其对轮毂整体性能的影响。

1 模型的建立

在此研究的是NSK第3代轮毂轴承单元，其由带凸缘外圈、带凸缘内圈、小内圈、滚子和密封装置组成，结构如图1所示。

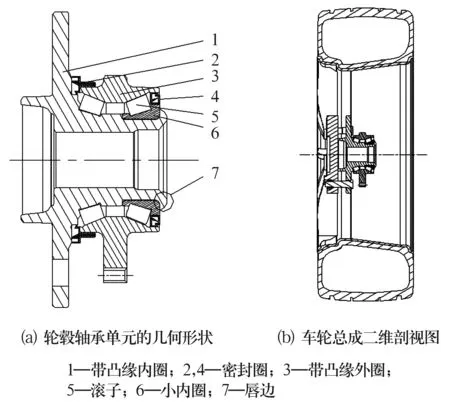
图1 轮毂轴承单元结构及安装示意图

1.1 实体模型的建立

为了保证模型分析时的真实性和完整性，在Catia环境中对车轮总成进行整体建模。在建立实体模型时，忽略小尺寸的圆角、倒角以及其他对分析结果影响不大的尺寸。整体建模如图2所示。图3为文中的主要研究对象，除在唇边处有差异外，其他相关尺寸参数全部相同。

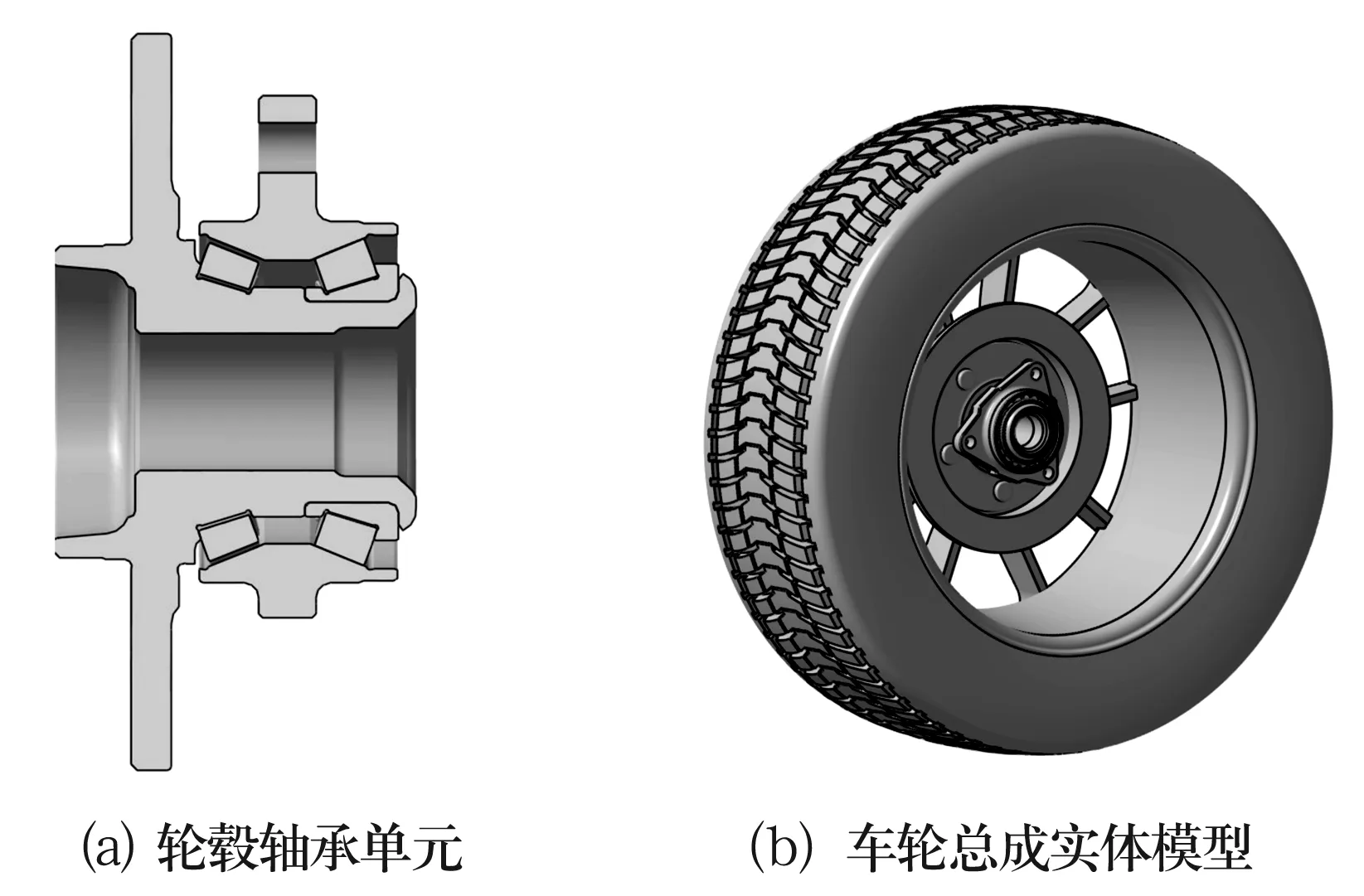
图2 车轮总成

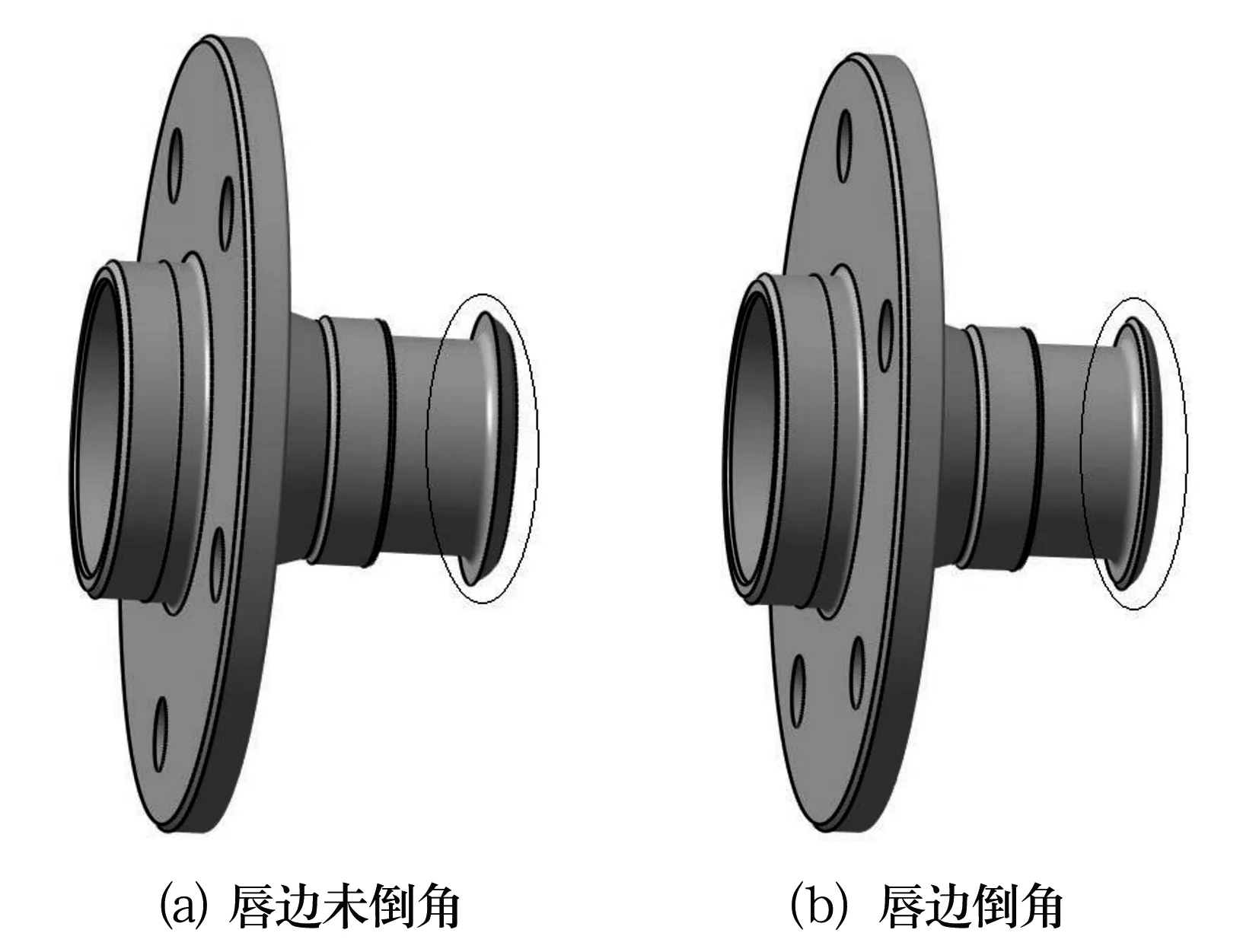
图3 带凸缘的内圈

1.2 有限元模型的建立

与经典的ANSYS相比，ANSYS Workbench 13.0操作界面更加友好，并且具有强大的材料库，可直接定义模型的相关性能参数，并可与其他三维建模软件进行无缝连接[8]，不会发生丢面、丢线等转换失败的情况，可直接进行应用分析，大大缩短了前期工作量。

1.2.1 材料的定义

在分析时，因为轮胎与轮辋部分只起到了传递力的作用，故对其不做具体分析。轴承小内圈、带凸缘的外圈和滚子的材料均为GCr15钢，带凸缘的内圈材料选用40Gr钢。其材料和力学性能参数见表1。

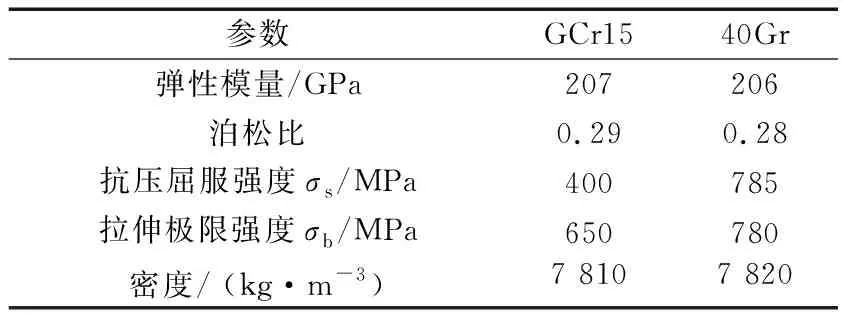
表1 主要材料及力学性能参数

1.2.2 接触类型的定义

一般情况下, 滚子与滚道之间的接触分析常存在计算过程复杂和计算结果不准确的问题[9]，因此按照ANSYS内部的接触向导对各个接触单元进行相应接触指定以提高计算精度。由于带凸缘的内圈与小内圈发生接触，属于柔体与刚体的面面接触，所以采用接触对的设置。一般设置有以下几个原则[10]：(1)若两个面网格大小不同，指定网格小的面为接触面，网格大的面为目标面；(2)若凹面与凸面发生接触时，指定凸面为接触面，凹面为目标面；(3)若两个面的面积相差较大时，指定面积小的面为接触面，面积大的面为目标面；(4)当两个面的刚度不同时，指定刚度小的面为接触面，刚度大的面为目标面。具体设置方法如下：小内圈内孔面为目标面，带凸缘内圈外圆面为接触面，采用绑定(Bonded)接触，忽略带凸缘内圈与小内圈之间的滑移，相当于小内圈与带凸缘内圈胶结在一起；小内圈右端面为目标面，带凸缘内圈唇部左端面为接触面，接触类型定义为粗糙(Rough)接触，以保证接触对法向可分离、不渗透且切向不滑动；由于不对其他零件进行具体分析，故将其接触对都定义为绑定约束(等同共用节点)，并不会影响最终分析结果。

1.2.3 网格划分

网格划分是建立有限元模型的重要环节。不同的网格划分，对计算的精度和规模将造成直接影响。由于采用六面体网格划分，会使计算精度更高，所以对带凸缘内圈进行六面体单元网格划分(Hex Dominant)，其他均采用自由网格划分(四面体网格)。为了进一步提高分析的准确性，接触面上均采用相同的网格密度划分。网格划分后的有限元模型如图4所示。其中总的节点数为730 996个，单元数为237 928个。

图4 网格划分模型

2 静力结构分析

2.1 定义边界条件

定义边界条件即给模型指定约束条件。由于带凸缘内圈主要用来传递转矩，而带凸缘的外圈需要与车架相连起支撑和定位的作用，因此将带凸缘外圈的3个螺栓孔面及其外端面进行全约束，如图5所示。

图5 约束的施加

2.2 受力分析及施加载荷

外部载荷通过轮胎施加在轮毂轴承上，即在轿车的实际行驶过程中，路面对轮胎的径向、轴向载荷等间接作用在了轮毂轴承上[6]。汽车转弯时，会产生较大的侧向加速度，由此产生的较大的侧向力将会直接作用在带凸缘内圈上。由于轮毂偏移量通常较小,径向载荷的作用点一般认为在两列轴承和作用点的中间位置[6]。轴承的载荷为[11]

(1)

(2)

式中：Fr为径向载荷，Fa为轴向载荷；“+”适用于外侧车轮；“-”适用于内侧车轮；W为车轴质量，kg；H，T分别为轿车质心高度和前轴轮距，mm；g为重力加速度，取9.81 m/s2；ag为侧向加速度，取最大值为0.55g。

经计算，某轿车前轮所受力为：Fr=13 978 N，Fa=9 785 N；轮胎气压为0.24 MPa。

模型的2个内圈滚道受到滚子的作用力，通过小内圈传递到带凸缘内圈的唇边。载荷施加方式如图6所示。

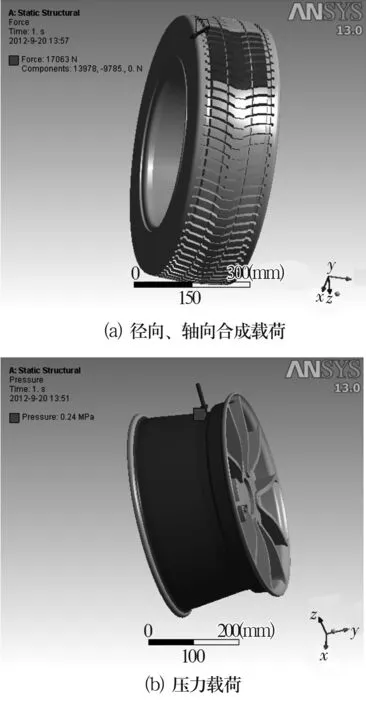
图6 载荷的施加

3 仿真结果与分析

通过计算可以分别获得带凸缘内圈内部等效应力分布云图及其应力值,如图7～图8所示。

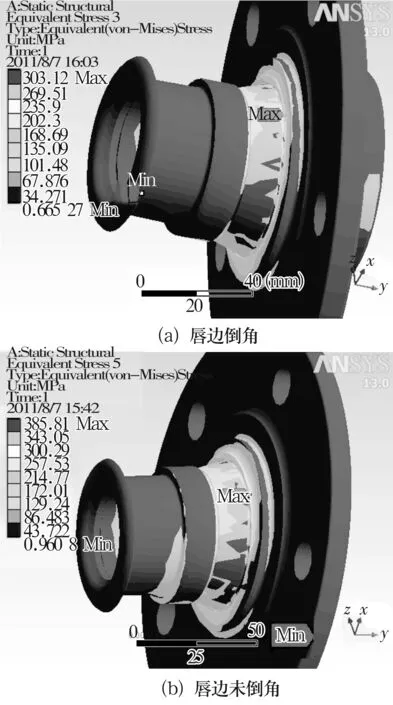
图7 轴向力由唇边指向凸缘的等效应力分布云图

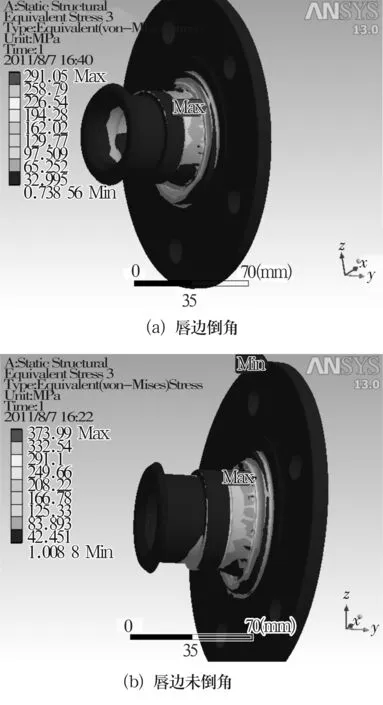
图8 轴向力由凸缘指向唇边的等效应力分布云图

仿真计算结果见表2。由表2对比分析可知：唇边倒角后，带凸缘内圈所受最大等效应力减小，最大等效应力出现在带凸缘内圈的根部，最大值为303.0 MPa，远小于材料的抗压屈服强度785 MPa。显然，带凸缘内圈倒角后可以有效降低内部的最大等效应力，延长轴承的使用寿命。因此，在保证轮毂轴承单元刚度稳定且最大等效应力不超过材料抗压屈服强度的情况下，为带凸缘内圈的优化提供了依据。

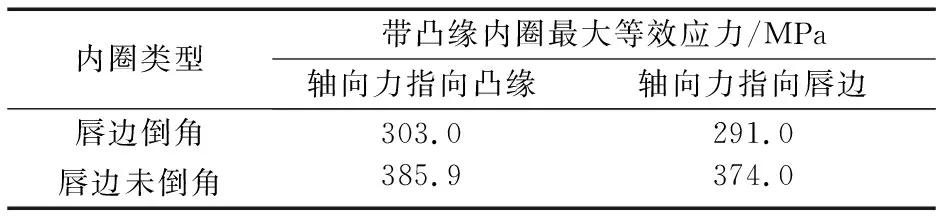
表2 带凸缘内圈应力计算结果

4 结论

(1)采用ANSYS Workbench软件成功对轮毂轴承单元结构强度进行了分析，并获得了带凸缘内圈的应力分布情况。

(2)通过控制倒角尺寸对唇边进行的优化设计，虽然增加了唇边的等效应力，但使带凸缘内圈的最大等效应力显著减小。