风电偏航轴承寿命计算与承载能力分析
凡增辉,李秀珍,谷小辉,欧阳华,朱为亮
(南车株洲电力机车研究所有限公司,湖南 株洲 412001)
风力发电机偏航轴承作为风力发电机(以下简称风机)迎风捕获能量的回转支承,安装于风机机舱底部,是偏航系统的关键部件。由于风机吊装维护费用极高,且风机工况复杂,偏航轴承一般承受较大的轴向力、径向力和倾覆力矩的联合作用,因此对偏航轴承的承载能力、寿命及可靠性提出了很高的要求。
目前主流的兆瓦级以上风机的偏航轴承主要采用四点接触球转盘轴承,因此对风机偏航轴承的设计计算大多运用经典的球轴承设计理论或者回转支承的设计方法[1-6]。但由于风机工况的特殊性与复杂性,风机偏航轴承的设计计算实际上有其独特的地方。下文综合运用球轴承的基本原理与风机设计的相关标准与规范,在基于风机真实工况与载荷的前提下,对风机偏航轴承的疲劳寿命与承载能力进行分析计算。
1 载荷工况
偏航轴承外圈与偏航制动盘一起固定在塔筒上,偏航轴承内圈与主框架通过螺栓连接(图1)。当偏航电动机工作时,带动主框架随着偏航轴承内圈旋转,从而使整个机舱和风轮处于最佳迎风状态。
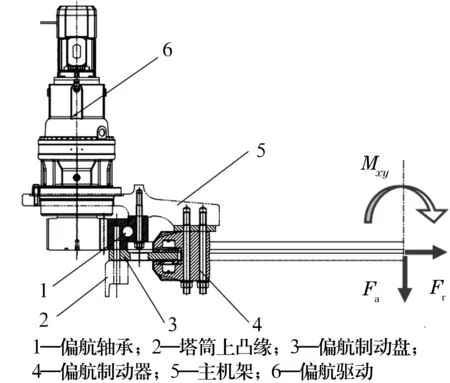
图1 偏航轴承安装示意图
在风机设计时,参照GL规范与IEC标准[7-8],运用行业通用的风机设计软件Bladed,对风机的各工况进行模拟计算,经过后处理,可以提取出针对偏航轴承坐标系下的载荷工况,如图2所示。
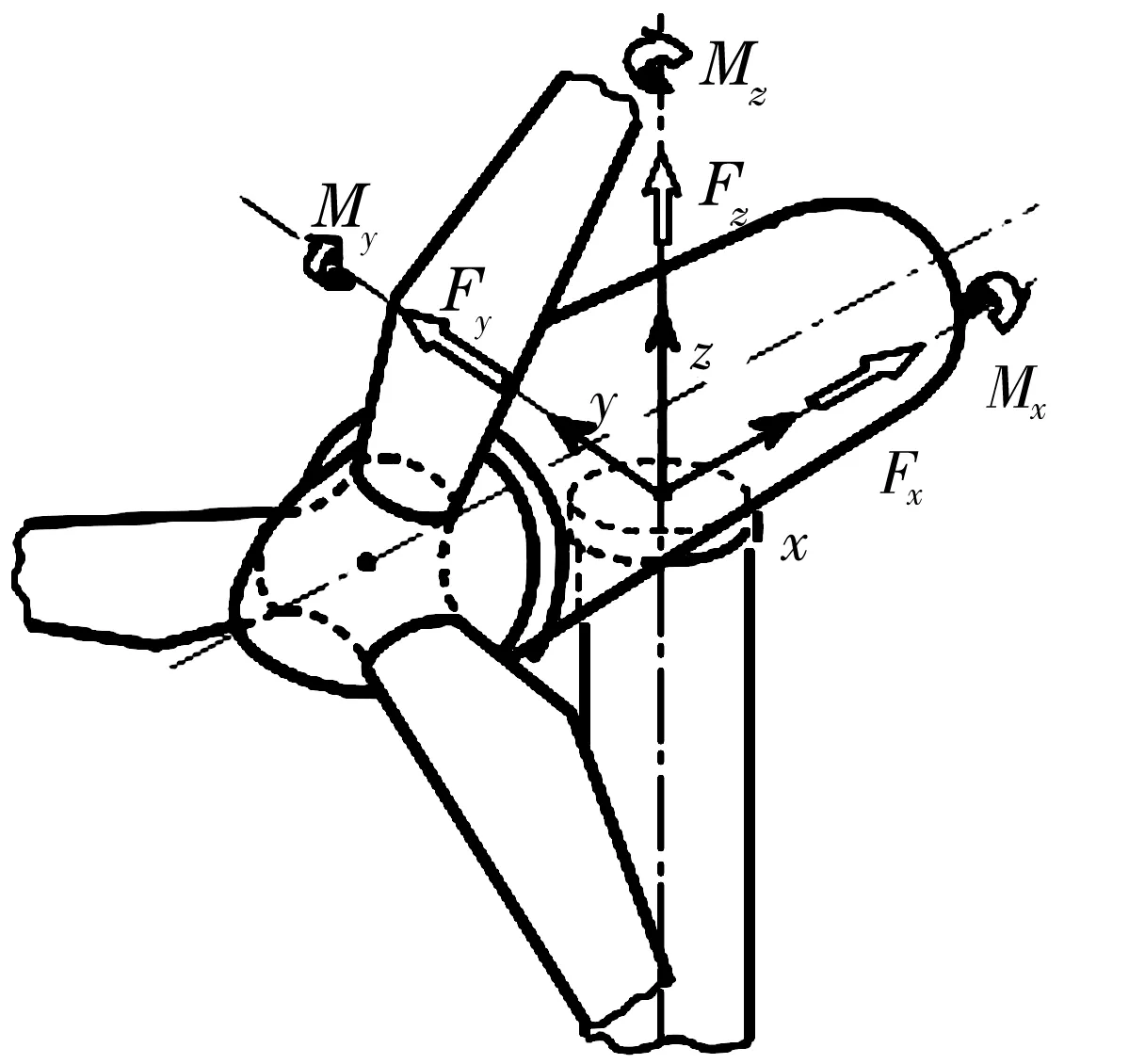
图2 偏航轴承坐标系示意图
图2中偏航轴承坐标系下的6个载荷分量依据偏航轴承的载荷特点可以简化合成为3个载荷:与Fz相等的沿z轴的轴向力Fa;由Fx,Fy合成的径向力Fr;由Mx,My合成的倾覆力矩Mxy,如图1所示(偏航轴承不承受Mz,因此,在此不予考虑)。
风机偏航轴承的承载能力与寿命主要考虑对象是沟道,且其承受的主要载荷为倾覆力矩,因此需要在Bladed软件中利用“Channel Combination”提取不同倾覆力矩Mxy的累积转数(或时间)分布统计,以计算偏航轴承全寿命周期内的等效疲劳载荷,如图3所示。为了使统计数据更保守,轴向力Fa和径向力Fr固定为最大倾覆力矩时对应的值。
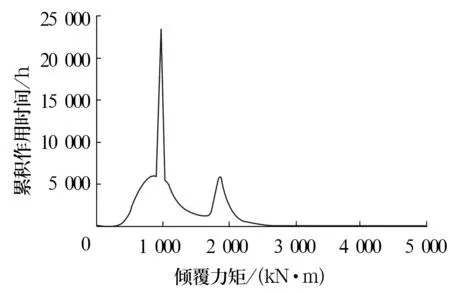
图3 偏航轴承倾覆力矩值的累积时间分布
而相对于疲劳载荷的统计处理,极限载荷的提取相对来说比较简单,即从Bladed后处理程序中提取各种工况下全寿命内最大Mxy对应的载荷即可,见表1。其中载荷工况中各工况具体描述见文献[8]。
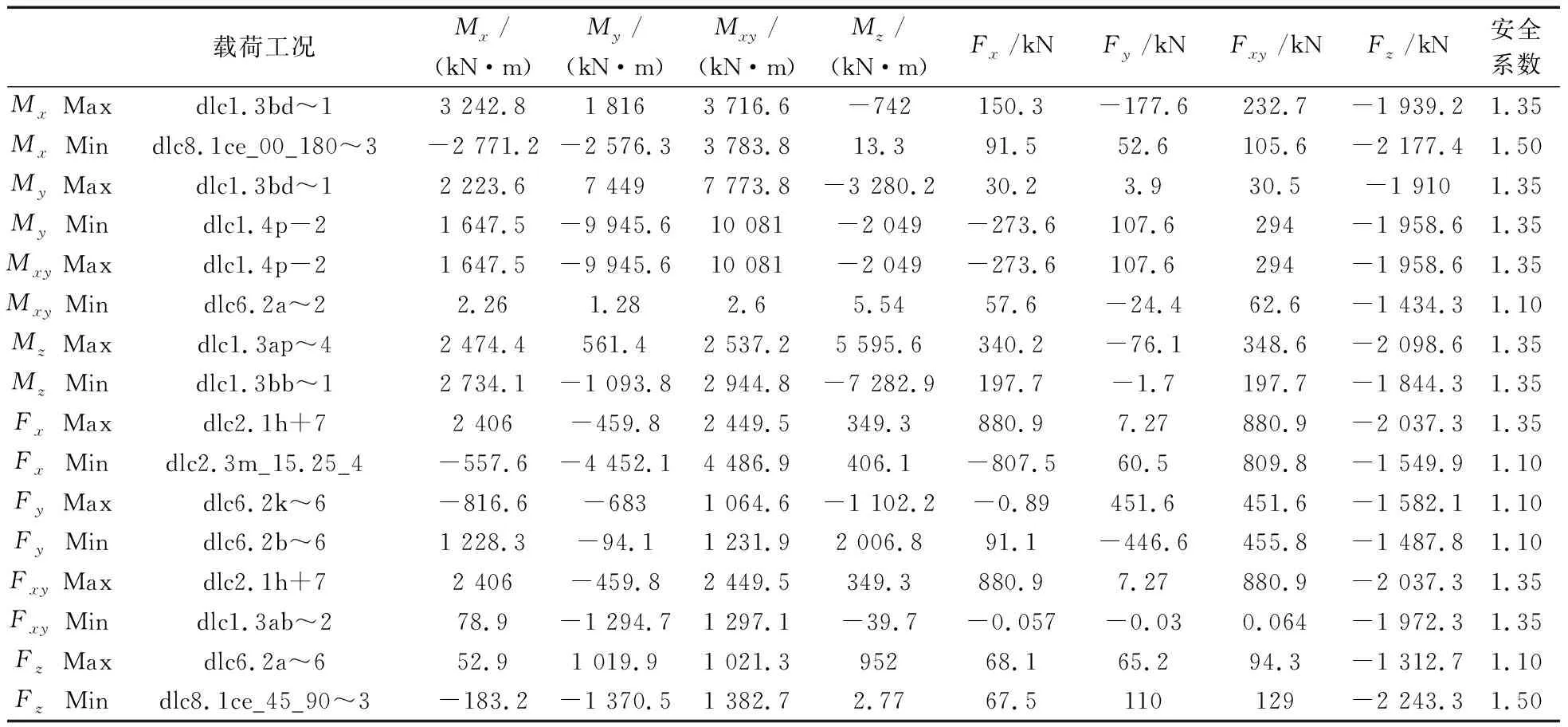
表1 偏航轴承中心极限载荷
2 寿命计算
2.1 理论分析
证明轴承拥有足够寿命的多数方法是运用数学方法估算其寿命。最典型的方法是运用Lundberg和Palmgren基于Weibull分布提出的寿命模型[9]。在该模型中,寿命的绝对值和离散度决定Weibull分布的曲线形状。从Lundberg和Palmgren的寿命试验结果可知,对于球轴承表达离散度的e值取10/9,Lundberg和Palmgren从理论与试验推导出如下关系
(1)
式中:p为寿命指数,对于球轴承p=3;P为当量动载荷。
对于(1)式,如将比例常数设为C,则(1)式为
(2)
式中:L10为基本额定寿命,106r(内圈转数);C为基本额定动载荷,在实际应用中,L10寿命用时间(h)表示时的关系式为
(3)
式中:n为轴承的转速, r/min。
2.2 基本额定动载荷
Lundberg和Palmgren将Hertz弹性接触理论与Weibull损伤概率理论相结合,并考虑了轴承的尺寸及应力循环次数的影响,在此基础上依据试验结果修正相关系数与指数,最终推导出了球轴承基本额定动载荷为
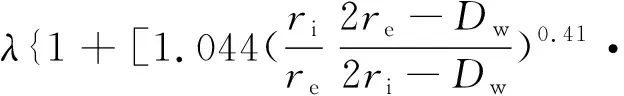
(4)
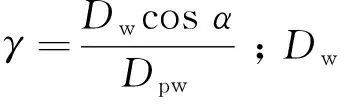
由于(4)式较为复杂,在ISO标准中将其进行了整理[10]。对于如偏航轴承等球径Dw>22.5 mm的轴承,
(5)
式中:bm为额定系数,对于偏航轴承,bm=1.3;fc为γ的函数,可通过文献[12]计算或查表插值得到。ANSI/ABMA标准[11]中,bm和fc被合并为fcm,从而得到基本额定动载荷的计算式为
C=3.647fcm(icosα)0.7Z2/3D1.4。
(6)
2.3 当量动载荷
Lundberg和Palmgren给出了将联合载荷换算成当量动载荷的计算式及其系数,其核心是通过轴承内部载荷分布与外载荷的静力平衡关系给出等效载荷。由于该关系式过于复杂,ISO等标准采用下列简化公式来计算当量动载荷
P=XFr+YFa,
(7)
式中:X,Y分别为径向、轴向载荷系数,可以依据ISO 281提供的数据查表得到。但如上文所述,偏航轴承主要承受的是倾覆力矩,如果依据(7)式推导当量动载荷,就需要将倾覆力矩转化为偏心轴向载荷。
在将倾覆力矩转化为偏心轴向载荷的方法上,还有基于相对偏心距,利用Simpson近似积分法通过积分参数获得当量动载荷的计算式
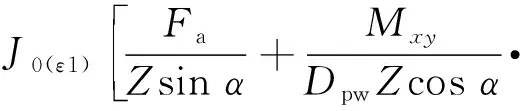
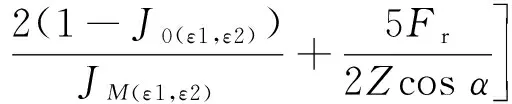
(8)
式中:J0(ε1),J0(ε1,ε2),JM(ε1,ε2)为载荷计算的积分系数[13]。显然,以上计算公式较为繁琐,在NREL提供的风机设计规范[14]中,提供了更为简便的计算公式,
(9)
3 承载能力
在风机设计时,由于20年设计寿命的考虑,常常需要考虑10年甚至50年一遇的极端风况的载荷影响,因此,在通过Bladed输出的风机载荷中,极限载荷与疲劳载荷的数值差距较大,如图3和表1所示。因此,对偏航轴承进行设计校核时需计算其静承载能力。
3.1 静态安全系数
轴承的静承载能力以滚动体允许的最大变形时的应力(对于球轴承,该值为4 200 MPa)与其实际承受的最大Hertz接触应力σmax的比值来衡量,因此,转盘轴承的承载能力一般用静态安全系数来衡量,表示为
(10)
(11)
式中:Qmax为偏航轴承最大滚动体载荷;a,b分别为Hertz接触椭圆的长、短半轴,可以通过计算曲率函数F(ρ)获得[9]。
依据IEC61400的要求,在进行风机结构设计的最大极限状态分析时,还需要考虑材料的不确定性和易变性,分析方法的不确定性以及失效时结构部件的重要性。因此,在针对偏航轴承的承载能力分析时,在(10)式的基础上还需要引入材料局部安全系数γm与重要失效系数γn进行修正,则
(12)
3.2 最大滚动体载荷
对于Fa,Fr及Mxy联合作用的偏航轴承的最大滚动体载荷,可通过下面方法求得。
Jones建立的载荷-位移关系为
Q=Klδl,
(13)
式中:Kl为轴承的载荷-位移系数;δ为接触变形量;l为载荷-位移指数。
建立以轴承相对轴向、径向与角位移为未知量的静力平衡方程为
(14)
(15)
(16)
式中:Qφ为位置角为φ的球的法向载荷。该方程的未知量可以用数值方法如Newton-Raphson法进行求解。获得轴承相对轴向、径向与角位移后,在φ=0处即可利用(13)式求得Qmax。
但是上面的计算方法过于繁琐,在NREL提供的风力设计规范里,提供了非常简单的最大滚动体载荷Qmax的计算公式
(17)
式中:Fr,Fa及Mxy选取表1中Mxy最大的一行数值。
4 工程示例
以某型号2.5 MW风机为例,其偏航轴承结构参数见表2。
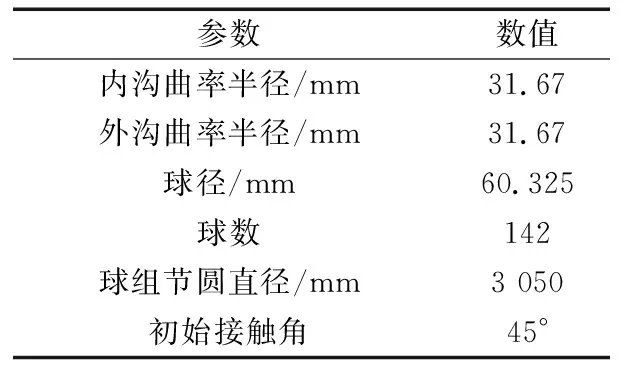
表2 偏航轴承结构参数
在进行当量动载荷计算时,需要用到图3所示的疲劳载荷(倾覆力矩Mxy)。依据GL规范的要求,在计算偏航轴承寿命时,需将疲劳载荷依据其作用的累积时间(或转数)分布进行等效,则等效疲劳弯矩Me为
(18)
式中:Mxyi为倾覆力矩Mxy的第i个值;ti为Mxyi作用的时间。
基于(5)~(6)式分别计算基本额定动载荷。利用(18)式计算出等效疲劳弯矩,分别基于(7)~(9)式计算当量动载荷,寿命计算结果见表3。
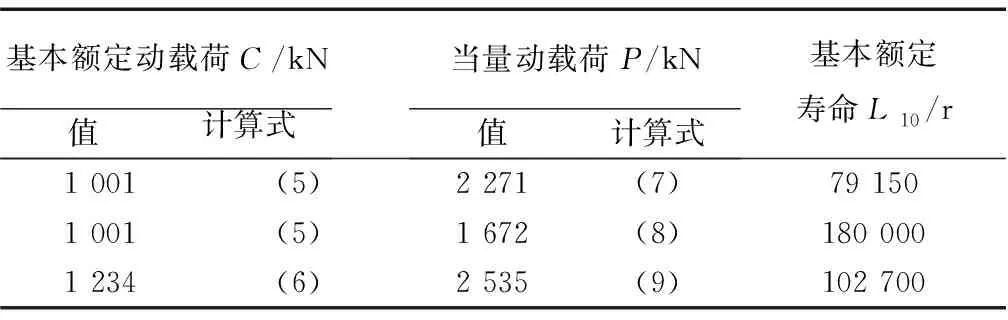
表3 寿命计算结果
根据实际运行统计,偏航轴承运行时间约为风机寿命的10%,结合偏航的速度,可以估算出在20年的设计寿命内,偏航轴承需要运行的转数约为55 000 r。从表3可知,所有计算方法的结果均大于该值,判定该偏航轴承寿命符合要求。
该型轴承的承载能力见表4。根据表4可以看出,在考虑了材料与失效安全系数的基础上,该偏航轴承的静态安全系数大于GL规范的要求值1.1,因此该偏航轴承的承载能力满足要求。

表4 承载能力计算结果
5 结束语
在综合考虑球轴承以及回转支承基本设计理念的基础上,结合风机行业的GL设计规范与ISO等标准,基于风机偏航轴承坐标系下的真实载荷工况,合理运用相关的计算方法,得到了完整的计算流程与较为准确的计算结果。
(1)偏航轴承疲劳载荷谱与其寿命计算强相关,需要依据偏航轴承坐标系下不同弯矩作用的累积转数的统计分布,按照GL规范的要求,将疲劳载荷平均等效。
(2)通过不同计算方法在工程实例中的应用可以看出,各种方法的计算结果虽有差异,但不影响对偏航轴承的基本判断,因此,可以采用文中较为简单的算法快速地对偏航轴承进行校核分析。

