函数解析的充要条件及Cauchy-Riemann方程的不同形式

程希伟

（淮南师范学院数学与计算科学系，安徽淮南232038）

函数解析的充要条件及Cauchy-Riemann方程的不同形式

程希伟

（淮南师范学院数学与计算科学系，安徽淮南232038）

解析函数是复变函数论中最基本的概念之一，在这里给出了五个函数解析的充要条件，还推导出函数解析的另一个充要条件，并探讨出Cauchy-Riemann方程另外两种形式.

解析函数；充要条件；柯西黎曼方程

1 五个常见充要条件

引理1函数在区域D内解析的充要条件是：二元函数u(x,y)，v(x,y)在区域D内可微且u(x,y)，v(x,y)在D内满足C.-R.方程.

引理2函数f(z)=u(x,y)+iv(x,y)在区域D内解析的充分必要条件是:ux,uy,vx,vy在D内连续且u(x,y)，v(x,y)在D内满足C.-R.方程.

引理3函数f(z)在区域G内解析的充要条件是：f(z)在G内连续；且对任一周线C，只要C及其内部全含于G内，就有

引理4函数f(z)=u(x,y)+iv(x,y)在区域D内解析的充要条件是：在区域D内v(x,y)是u(x,y)的共轭调和函数.

引理5函数f(z)=u(x,y)+iv(x,y)在区域D内解析的充要条件是：f(z)在D内任一点a的邻域内可展成z-a的幂级数.

2 函数解析另一个充要条件

函数f(z)=u+iv解析的充分必要条件fz¯=0.

证明必要性

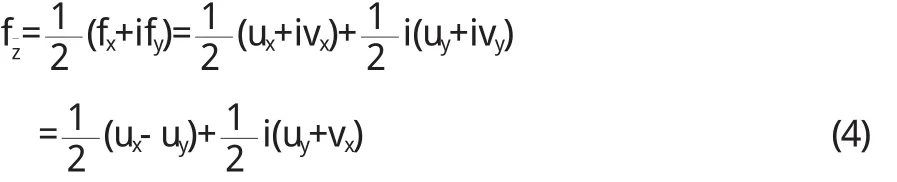
而f(z)是解析函数，由C.-R.得，ux-vy=0，uy+vx=0,代入(4)即fz¯=0.

必要性:

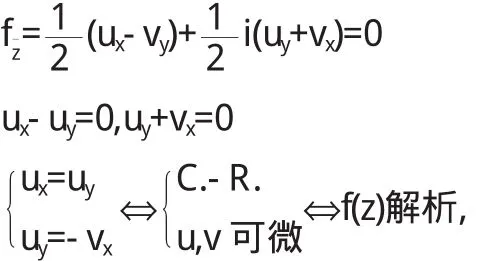
证毕.

3 Cauchy-Riemann方程另两种形式

3.1 极坐标下的柯西黎曼方程为

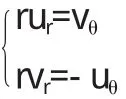
证明若f(z)=u(r,θ)+iv(r,θ) z=reiθ=r(cosθ+isinθ)=x+iy f(z)=u(r,θ)+iv(r,θ)

而f(z)=p(x,y)+iq(x,y)解析，C.-R.方程为px=qy；py=-qx即

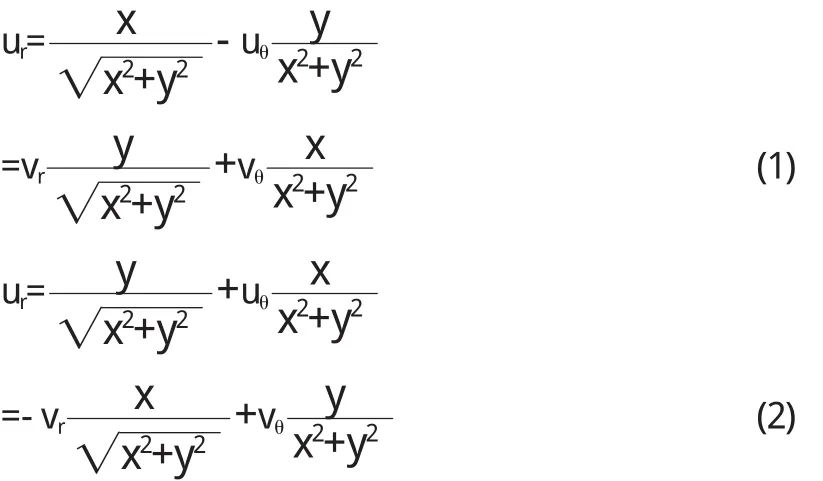
3.2 Cauchy-Riemann方程的梯度形式

f(z)=u(x,y)+iv(x,y),u(x,y)v(x,y)的Cauchy-Riemann方程的梯度形式为

证明在代数形式下的柯西黎曼方程为ux=vy，uy=-vx，那么有

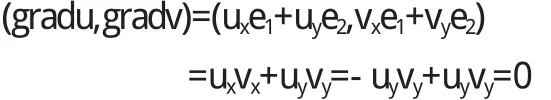
其中e1,e2是与x,y轴正向相同的单位矢量.

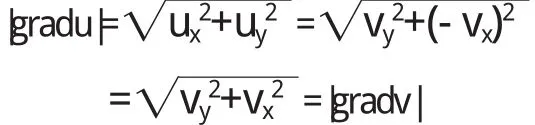
4 求解析函数的一种公式

已知调和函数v(x,y)，以v(x,y)为虚部的解析函数

证明因为v(x,y)是调和函数，共轭关系知存在u(x,y)使得f(z)=u+iv在D内解析，取D内任一点z0，那么f(z)在z0的某一邻域内

将(5)(6)代入(4)中有

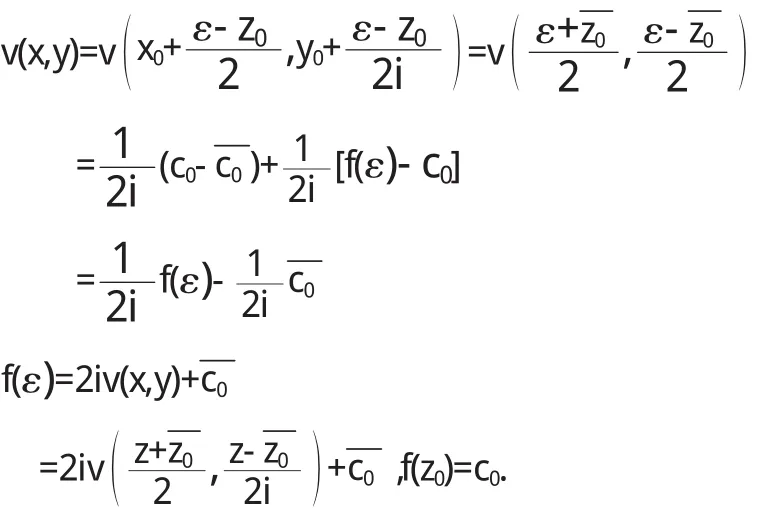
将ε换成z得出以下结论

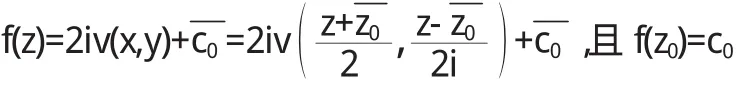
同理有已知u(x,y)是单连通区域D内的调和函数，z0为D内任一点，则在D内以u(x,y)为实部的解析函数为

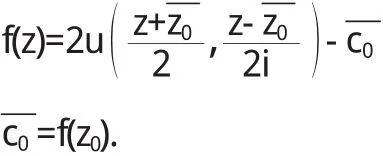
〔1〕钟玉泉.复变函数论[M].北京：高等教育出版社，2004.

〔2〕杨纶标，郝志峰.复变函数[M].北京：科学出版社，2003.

O174.5

A

1673-260X（2013）07-0007-02