基于LS-SVM的无轴承同步磁阻电动机逆模型辨识及解耦控制

杨泽斌，汪明涛，孙晓东，朱熀秋

(江苏大学 电气信息工程学院，江苏 镇江 212013)

1 前言

无轴承同步磁阻电动机(bearingless synchro-nous reluctance motor,BSRM)将磁轴承与同步磁阻电动机融于一体，实现电磁转矩与径向力的集成化与一体化，具有高转速、无磨损、无润滑和寿命长等普通电动机不具有的优点，在高速机床、飞轮储能、涡轮分子泵及离心压缩机等领域有广泛的应用空间[1-2]。

BSRM与其他类型无轴承电动机相比，由于转子没有永磁体，也不需要励磁绕组，结构简单，运行可靠，成本低廉。因其可以实现较高的凸极比，从而具有转矩密度高、动态响应快、转矩脉动小和功耗低等优点，在高速高精应用领域具有独特优势[3-4]。

BSRM是一个非线性、多变量和强耦合的复杂系统，要实现稳定悬浮与可控旋转，必须实施电磁转矩与径向悬浮力之间的动态解耦。文献[3]分析了BSRM的基本结构与运行机理，指出电动机能稳定可靠悬浮工作的核心是控制系统设计。文献[4]采用前馈补偿设计了解耦控制系统，由于直接采用给定电流参与解耦计算，解耦精度较差，引起闭环动态性能下降。文献[4]同时指出，BSRM径向力和电动机绕组电流的线性关系受磁饱和影响较大，当电动机绕组中电流达到一定值后，反而随电流增加而下降。因此，这种基于线性方法设计的补偿解耦方法，在电动机饱和运行区域控制性能欠佳。文献[5]提出一种改进的BSRM数学模型，通过在线查表与参数检测，达到减小磁饱和及径向悬浮力和转矩之间耦合的目的。但是上述文献提出的解耦方法本质上只是实现了悬浮力与电磁转矩的静态解耦，并没有实现完全意义上的动态解耦。

近年来，逆系统成为非线性解耦控制的一种有效方法[6]，但是传统逆系统在实际工程中碰到2个瓶颈:(1) 逆系统方法要求被控对象数学模型与参数精确已知，这在实际工程中几乎是不可能的；(2) 逆系统需要求解出逆模型的解析表达式，对于复杂被控对象很难或无法满足。为此，有学者将神经网络的学习能力与逆系统结合，在初定逆系统基本结构的基础上，采用神经网络离线辨识被控对象的逆模型，并实施在线解耦控制，取得了很好的控制效果[7]。但理论分析与数据试验表明，神经网络收敛速度慢，泛化能力弱，结构确定难，容易陷入局部最小，限制了其使用范围。与神经网络相比，采用结构风险最小化准则的支持向量机具有小样本学习、训练速度快、泛化能力强、拓扑结构固定等优点，在实际问题中具有更好的应用前景[8-10]。下文在建立BRSM数学模型基础上，提出了BSRM的LS-SVM逆模型辨识与动态解耦控制策略。基于Interactor算法[11]，在分析逆系统存在的基础上，利用LS-SVM的函数拟合能力，离线建立了BSRM逆模型；将逆模型与原系统串联，将原非线性系统线性化解耦为3输入3输出的伪线性系统，并构造了PID反馈控制器。

2 BSRM数学模型与可逆性分析

2.1 BSRM数学模型

对于转子质量为m，凸极弧度角为30°，转矩绕组极对数PM=2，悬浮力绕组极对数PB=1的BRSM，在忽略磁饱和情况下，作用在转子单位表面积上的Maxwell力为

(1)

其沿x，y方向上的Maxwell力分别为

(2)

式中：B为磁感应强度；θ为转子机械角度；μ0为真空磁导率；A为有效面积；l为电动机有效铁芯长度；r为转子凸极半径。

假定转子偏心位移远小于气隙长度[12]，且仅考虑转子凸极区域有效部分，在凸极区域进行分段积分。为了进一步简化表达式，将磁通势用电流及线圈匝数表示，将电流矢量转化到d-q同步旋转坐标系下，得到x，y方向径向力分别为

(3)

式中:id，iq分别为同步旋转坐标系下转矩绕组等效两相电流;ix，iy分别为同步旋转坐标系下悬浮力绕组等效两相电流；N1,N2分别为转矩绕组与悬浮力绕组每相串联有效匝数；δ0为平均气隙长度。

当转子偏心时，受到的Maxwell张力为

(4)

式中：k为与电动机结构有关的比例参数；x，y为转子径向偏移量。假定转子沿x，y方向施加的径向载荷分别为Fzx，Fzy，m为转子质量，则可建立的转子径向力子系统的运动方程为

(5)

BRSM定子电压方程为

(6)

定子磁链方程为

(7)

转矩方程为

(8)

旋转运动方程为

(9)

式中：ud，uq为定子电压d-q轴分量；Rs为定子每相电阻；Ld，Lq分别为d-q轴电感；Ω为同步角速度；Ψd，Ψq为定子磁链d-q轴分量；J为转子转动惯量；pm为电动机转矩绕组极对数；Te，TL分别为电动机电磁转矩和负载转矩。

2.2 复合被控对象的状态方程

BRSM的完整数学模型极其复杂，但如果将BRSM与供电的三相逆变器及其附加电路看作一个复合的被控对象，就可以在悬浮力系统运动方程与旋转运动方程的基础上，简化其数学模型，复合被控对象示意图如图1所示。

图1 BRSM复合被控对象

在d-q同步旋转坐标系下，选择BRSM复合被控对象状态变量

ξ=[ξ1ξ2ξ3ξ4ξ5]T=

(10)

系统输入变量

u=[u1u2u3]T=[iqixiy]T，

(11)

系统输出变量

η=[η1η2η3]T=[xyω]T，

(12)

建立复合被控对象的状态方程

(13)

系统输出方程η=h(ξ)，即

(14)

2.3 模型可逆性分析

由系统状态方程和输出方程可以看出，系统为5阶3输入3输出的非线性、强耦合系统，直接线性化并实施闭环控制难度很大。如果能使用α阶逆系统理论构造出原系统的逆系统，并将其串联在原系统之前，则原系统被线性化解耦为3个相互独立的线性积分系统，再运用线性系统理论实施闭环控制。

首先计算输出η=h(ξ)对时间的导数，直至显含输入变量u[11]，得到

(15)

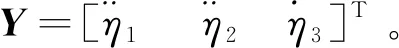
从而得到系统的Jacobi矩阵为

(16)

经计算可得

(17)

Jacobi矩阵A非奇异，系统可逆，同时相对阶为α=[α1α2α3]T=[2 2 1 ]T，逆解析形式为

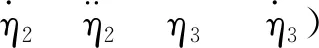
(18)

3 BRSM的逆模型辨识与解耦控制

3.1 LS-SVM辨识原理

给定n组训练样本(xi,yi)(i=1,2,…,n)， 输入为xi∈Rm，输出为yi∈R，LS-SVM的目的是确定函数

y(x)=ωTφ(x)+b，

(19)

对未知函数进行估计，其中权向量ω∈Rm，偏置值b∈R。非线性映射φ(x)将样本从原空间映射到高维特征空间。

LS-SVM的训练可以通过求解以下最优化问题来完成

(20)

yi=ωTφ(xi)+b+εi,i=1,2,…，n,

式中：γ为正则化参数(惩罚因子)；εi为不敏感损失函数的松弛因子。

引入Lagrange乘子ai，将(20)式的约束优化问题转化为无约束问题

(21)

其中a=(a1,a2,…，an)T，ω=(ε1,ε2,…，εn)T。

根据KKT条件，将Lagrange函数对ω，a，b，ε分别求偏导，可以将优化问题转变为以下线性方程组的求解问题

(22)

其中K(xi,yj) 为满足Mercer条件的核函数，常用的有多项式、径向基函数(RBF)、Sigmoid 函数等多种形式。考虑到RBF 核函数具有参数容易选择、易于实现和辨识效果好等优点，文中选择RBF核函数。

(23)

式中：σ为核宽度，反映了边界封闭包含的半径。

基于上述最小二乘法(22)式求解a与b，再由(21)式求出ω，就可以得出(xi,yi)拟合方程为

(24)

由 (24)式可知，LS-SVM函数拟合结构如图2所示。

图2 支持向量机函数拟合结构图

3.2 BRSM的LS-SVM逆模型辨识

采用LS-SVM辨识逆模型，可以突破传统逆系统控制方法的技术瓶颈，使得复杂非线性系统的逆控制成为可能。一方面，用支持向量机逼近逆模型，可以有效解决解析逆矩阵无法求取的难题，同时可以有效克服神经网络收敛速度慢，容易陷入局部最小及网络拓扑结构难以确定等难题。

LS-SVM逆模型辨识步骤如下。

(2) 离线建立逆模型。根据采样数据建立的训练样本集，采用最小二乘算法(22)式对3个支持向量机进行离线学习，获得相应的a与b，从而建立支持向量机逆模型。

3.3 BRSM的LS-SVM逆解耦控制

将训练好的逆模型作为前馈控制器与原系统串联，构成3个相互独立的伪线性系统，传递函数分别为Gx(s)=s-2，Gy(s)=s-2，Gω(s)=s-1，如图3所示。

图3 支持向量机逆线性化解耦示意图

这样，一个复杂非线性系统控制问题就转换成简单的线性系统控制问题。综合考虑响应速度、控制精度、承载能力和稳定性等因素，设计带微分限制环节与积分分离算法的PID控制器作为反馈环节，其传递函数为

(25)

式中：TD为微分时间常数；KP为比例系数；TI为积分时间常数；ε为微分增益；e为输入静差；c为设定阈值。

PID反馈控制器与支持向量机逆前馈控制器构成复合控制器，与被控对象组成闭环控制系统，结构如图4所示。

图4 BRSM闭环控制系统

4 系统仿真与分析

为了验证BRSM支持向量机逆模型辨识与解耦控制效果，采用Matlab/Simulink搭建仿真平台，对系统的拟合输出特性、BRSM转子起浮特性与转速响应、转速突变的位移和转速特性进行了仿真试验。 无轴承同步磁阻电动机样机转矩绕组参数为：极对数PM=2，Ld=0.035 H，Lq=0.007 H，Rs1=0.25 Ω。悬浮力绕组参数：PB=1，d-q轴电感Lx=Ly=0.02 H，Rs2=0.15 Ω。转子参数：质量m=1 kg，转动惯量Jz=1.356×10-4kg·m2，Jx=Jy=2×10-3kg·m2，气隙长度δ0=0.25 mm。

采用1 500组数据对支持向量机进行拟合训练后，用500组数据验证支持向量机逆拟合结果，拟合相对误差如图5所示。最大相对误差为2.9%， 平均相对误差为1.8%，达到了很好的拟合效果。

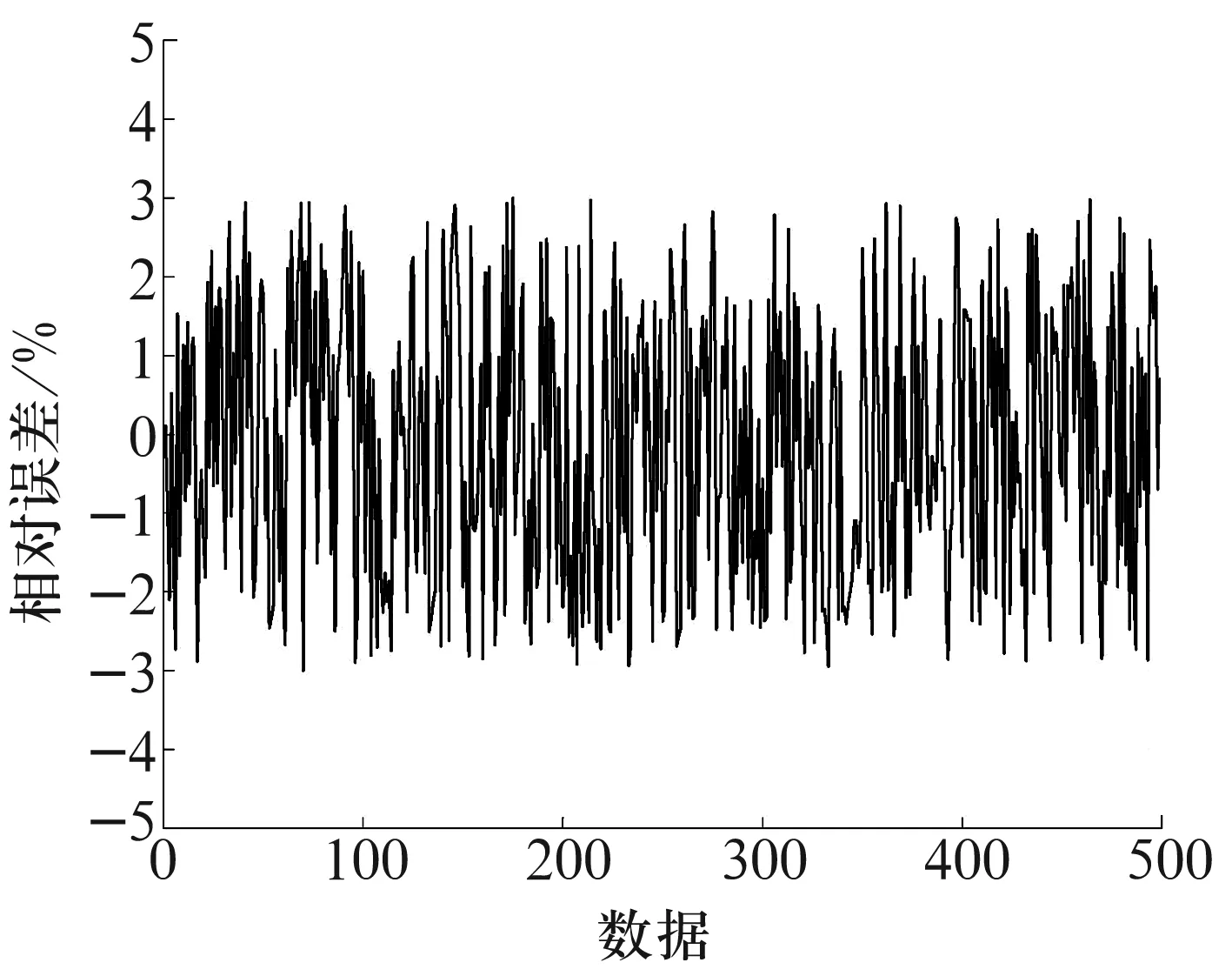
图5 支持向量机逆拟合相对误差

仿真步骤为，给定转子初始位置后空载启动，将速度调至5 000 r/min，研究闭环系统的动态响应性能。在稳定悬浮后突变径向位移给定，验证闭环解耦效果与鲁棒性。

图6为电动机静止状态下空载启动至稳定悬浮于5 000 r/min时的转子起浮运动轨迹，转子质心初始位置为x0=-0.1 mm，y0=-0.1 mm。给定位置为x*=0，y*=0。计算得位移调节时间小于0.04 s ，超调量δ小于2%，无稳态误差。

图6 转子起浮轨迹

电动机的速度响应曲线如图7所示，可以看出，速度调节时间小于0.2 s，超调量δ小于1% ，系统响应速度快，动态性能好。

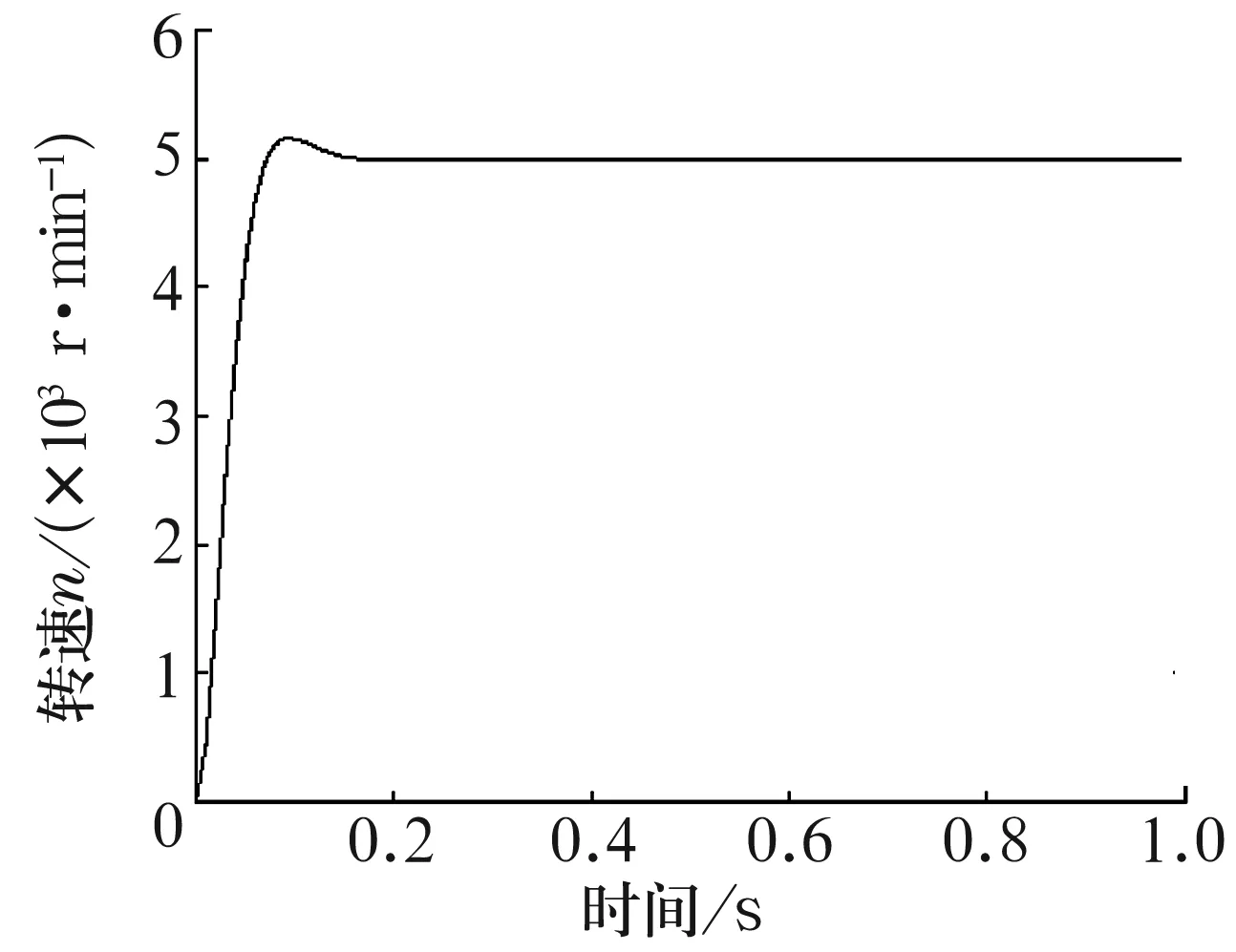
图7 转速响应曲线

为了检验闭环控制系统的动态解耦效果与鲁棒性能，转子质心初始位置设定为x0=0，y0=0，转速n0=0，转子位置给定值设为x*=0.1 mm，y*=0 mm，转速给定值n=5 000 r/min。在t=0.5 s时转子位置给定值突变为x*=-0.1 mm，y*=0，转速给定值不变。在t=1 s时转子位置给定值突变为x*=-0.1 mm，y*=0.1 mm，转速给定值不变。在t=1.5 s时转子位置给定值不变，转速给定值突变为n=6 000 r/min。质心移动轨迹和转速轨迹如图8所示，可以看出，当位置给定值突变时，转子在经过小幅震荡以后，很快稳定悬浮在给定位置，在此期间，另一方向位置及转速保持不变；当转速给定值突变时，转子转速亦能快速跟踪到给定值，并保持转子位置不变，表明闭环系统具有良好的动态解耦效果和鲁棒性。

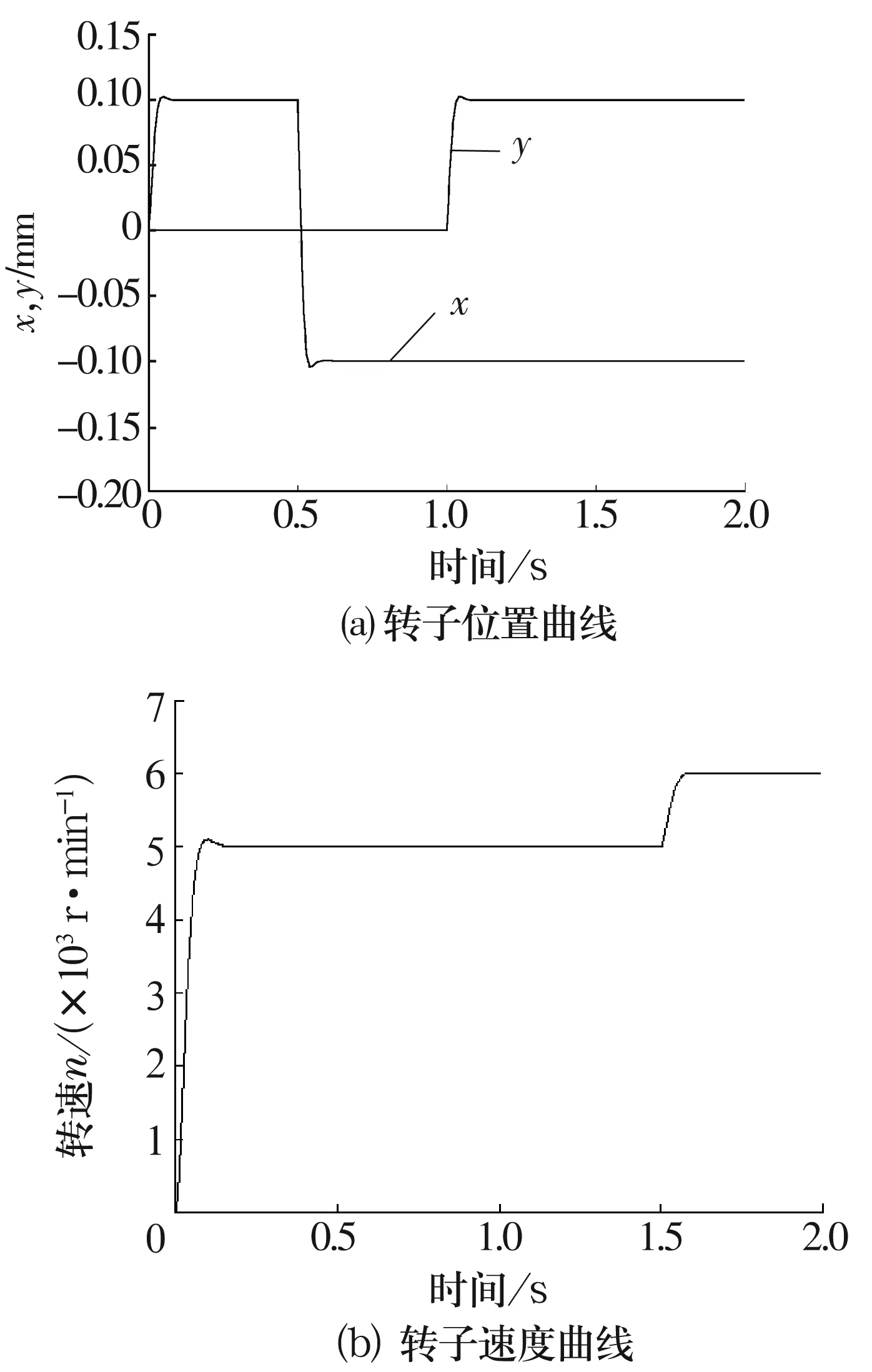
图8 突变给定下的系统响应

5 结论

为有效解决BSRM这一非线性、强耦合的多输入、多输出系统的动态解耦问题，提出了基于LS-SVM逆模型辨识与动态解耦控制策略，得到以下结论：

(1) BSRM是一个3输入3输出的5阶非线性、强耦合复杂系统，而且BSRM系统是可逆的；

(2) LS-SVM逆模型辨识方法不需要系统的先验知识，可以在不依赖BSRM精确数学模型的前提下，很好地完成BSRM逆模型辨识，从而突破了传统逆系统方法的2个瓶颈；

(3) LS-SVM逆解耦控制方法结合了LS-SVM的非线性回归能力与逆系统方法线性化解耦的优点，可以将BSRM系统解耦为伪线性系统，实现了BSRM转速、x轴及y轴径向位移的线性独立控制，同时设计的闭环控制系统具有超调量小、控制精度高、响应速度快和抗干扰能力强等优点。