基于时频单源点的欠定混合矩阵估计

董天宝，程雷，杨景曙

1.电子工程学院702室，合肥 230037

2.总参陆航部军代局，北京 100050

基于时频单源点的欠定混合矩阵估计

董天宝1，程雷2，杨景曙1

1.电子工程学院702室，合肥 230037

2.总参陆航部军代局，北京 100050

1 引言

盲源分离主要研究在混合信道和源信号都未知的情况下如何从观测信号分离出源信号，已经在许多领域取得了较好的应用。当传感器个数小于源信号个数时的盲源分离称为欠定盲源分离，是近几年盲信号处理领域的一个热点研究问题。欠定盲源分离问题的线性瞬时混合模型可以表示为：

其中，x(t)=[x1(t)，x2(t)，…，xM(t)]Τ表示在时刻t大小为M×1的观测信号矢量，A=[a1，a2，…，aN]∈RM×N(M〈N)是混合矩阵，ai表示混合矩阵的第i个列矢量，s(t)=[s1(t)，s2(t)，…，sN(t)]Τ表示时刻t大小为N×1的源信号矢量，n(t)表示加

性高斯噪声。式（1）还可以表示为：

为分析方便，暂不考虑噪声的影响，于是无噪声时欠定盲源分离的线性瞬时混合模型可以表示为：

目前，稀疏分量分析是解决欠定盲源分离问题的主要方法。稀疏分量分析通常采取两步法，即首先估计混合矩阵，然后在混合矩阵已经估计出来的基础上实现源信号的分离。与独立分量分析方法相似，混合矩阵估计的好坏直接影响后面的信号分离效果。因此，研究混合矩阵的估计问题是很有意义的。

在稀疏分量分析中，对混合矩阵的估计主要是利用信号的稀疏性。以时域信号分析为例，假设在t时刻只有第i个源信号存在，则式（3）退化为：

由此可知，此时观测信号矢量与混合矩阵的第i个列矢量的方向相同，在不考虑幅度差异的情况下，估计出了混合信号矢量的方向，也就实现了对混合矩阵第i个列矢量的估计。在信号充分稀疏的条件下，通过聚类或其他方法检测出所有这样的方向矢量，就实现了对混合矩阵的估计。然而，信号在时域通常很难满足稀疏性的条件。很多学者研究发现，有的信号在时频域会表现出较好的稀疏性，如语音信号等。因此，可以在时频域中采用稀疏分量分析实现对混合矩阵的估计。

在只有一个信号的时频点，观测信号列矢量具有较好的方向聚集性，该方向对应混合矩阵的一个列矢量。在实际中，很难满足在所有的时频点上都只有一个源信号存在，于是对应的观测信号列矢量的聚集性会大大减弱，从而影响了混合矩阵估计的精度。如果能够检测出所有只有一个信号存在或者只有一个信号起主要作用的时频点，将会提高混合矩阵的估计精度。很多学者在这一方面作了相关研究。文献[1]所提出的ΤIFROM算法通过检测各路观测信号的时频比在连续几个时频窗中是否恒定来提取时频单源区域。文献[2]首先计算观测信号的时频比矩阵，然后通过检测具有相同列矢量的子矩阵实现对时频单源点的检测。刘琨等[3]利用时频单源点所对应的观测信号时频比的模值和相角近似相等的特点，实现时频单源点的提取。文献[4-8]则是利用观测信号的协方差矩阵检测时频单源点。谢胜利等[9]利用相邻两个时频点构造了一个函数，然后通过检测这个函数值来提取时频单源点。文献[10]通过比较两个连续时频窗对应的观测信号向量模值的方向实现对时频单源点的检测。文献[11]也是先计算各路观测信号的时频比，根据时频单源点对应的时频比为实数这一特性来检测时频单源点。

针对欠定盲源分离中的混合矩阵估计问题，本文提出了一种新的时频单源点检测方法，该方法不需要计算观测信号的时频比矩阵，也不需要计算观测信号的协方差矩阵，计算复杂度大大减小。同时该方法不要求时频单源点必须处于连续的时频窗中。在检测出时频单源点后，采用K-means聚类方法得到混合矩阵的初步估计值。然后，去除每一类数据中偏离中心较远的数据，最后得到混合矩阵的估计。

2 时频单源点检测

其中X(t，f)表示观测信号的傅里叶系数，Si(t，f)表示第i个源信号的傅里叶系数。假设在某个时频点(tp，fp)处只有一个信号si存在，其他信号的傅里叶系数都为0，则式（5）可以写为：

对式（3）两边进行短时傅里叶变换（SΤFΤ），可以得到：

式（6）中的X(tp，fp)和Si(tp，fp)都是复数形式，令式（6）两边的实部和虚部对应相等，可得：

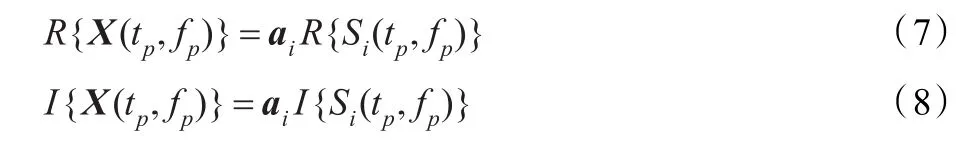
其中R{X(tp，fp)}和Ι{X(tp，fp)}分别表示观测信号向量X(tp，fp)的实部和虚部。分别对得到的实部和虚部进行归一化处理得：

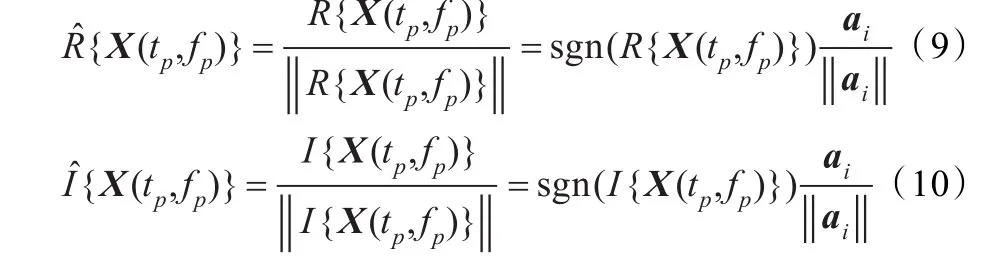
对实部和虚部进行归一化处理得：

由式（14）和（15）可知，在时频点(tq，fq)处，当下面的条件满足时，归一化后的观测信号向量的实部和虚部相等。

图1 时频单源点检测前后两路观测信号的散点图

即使采用前面所述的映射处理，式（16）～（18）同时发生的概率也是很小的。同理，如果在时频点(t，f)处有多个信号同时存在，可以得到相似的结论。因此，可以通过在每个时频点检测经过映射处理后的归一化观测信号向量的实部和虚部是否相等来判断该时频点是否为时频单源点。本文采用欧几里德范数作为两个向量是否相等的度量准则，于是满足下面等式的时频点即为时频单源点。

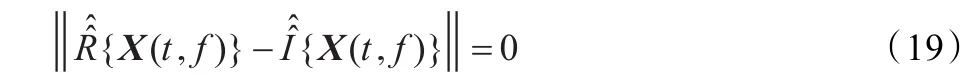
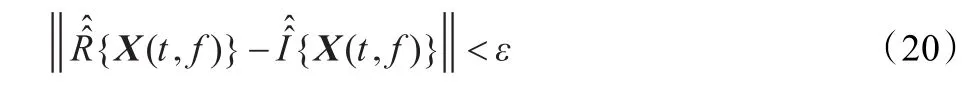
通过检测时频单源点，使观测信号向量的方向聚集性大大增强，有助于后面对混合矩阵列矢量的估计。图1是由6个源信号混合得到的两路观测信号对应的时频域散点图，图1（a）是时频单源点检测前，两路观测信号的短时傅里叶变换系数对应的散点图，由图可知，虽然能看出有6条直线，但每条直线的方向并不是很明显。图1（b）是使用本文的时频单源点检测方法后对应的时频域散点图，由图可见，每条直线的方向更加清晰。此外，本章提出的时频单源点检测方法运算量与时频点数量大小呈线性关系，运算复杂度为O(N)，因此运算速度较快。

3 利用时频单源点估计混合矩阵

在得到时频单源点后，下面的任务就是估计混合矩阵。在前一章中，观测信号向量进行了归一化处理，为了减小散点图中心点附近的点对混合矩阵估计的影响，去除散点图中原点附近那些幅值较小的时频点。

在经过了上面的预处理后，对剩下的时频点采用K-means方法进行聚类分析，得到的每一个聚类中心对应混合矩阵的一个列矢量。时频单源点对应的散点图中直线已经具有了较好的方向性，即使这样，在散点图中仍然会有一些点不在直线对应的主方向上，这些点会对直线方向的估计产生不利影响。为了提高混合矩阵的估计精度，对聚类分析得到的每一类数据作进一步处理，首先得到每一类数据的中心点，假设得到的一类数据集为{X1，X2，…，XN}，其中Xi表示一个时频点对应的时频域观测信号矢量，N代表数据集中数据的个数。则该类数据集的中心点为：

通过下面的式子计算该数据集中的每个数据点与中心点的夹角。

设一个门限β〉0，去除那些与中心点夹角较大的数据点，即去除那些满足下面式子的数据点：

然后利用式（21）计算剩下数据点的中心点，该中心点就是混合矩阵的一个列矢量的最终估计值。

4 欠定混合矩阵估计算法步骤

下面将本文提出的混合矩阵估计算法步骤总结如下。

（1）去除散点图中原点附近的观测信号数据。

（2）对观测信号矢量进行归一化和映射处理。

（3）通过式（20）检测时频单源点。

（4）采用K-means方法对得到的时频单源点数据进行聚类分析。

（5）对聚类分析后得到的每一类数据进行处理，去除那些偏离中心方向较远的数据点。

（6）重新计算每一类数据的中心，得到混合矩阵的估计值。

5 仿真实验

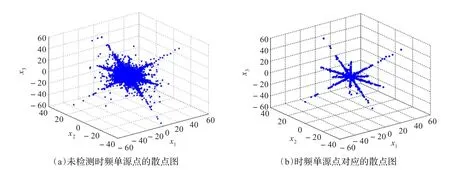
图2 时频单源点检测前后的散点图（三路观测信号、五个源信号）

为了评估混合矩阵估计算法的性能，采用泛化交扰误差（Generalized Crosstalking Error，GCE）[12]作为评价准则。GCE定义如下：

其中A表示真实的混合矩阵，A~表示混合矩阵的估计值，Π表示N×N可逆矩阵集合，这些矩阵的每一列只有一个非零元素1。如果GCE=0，表示估计得到的混合矩阵与真实矩阵完全相同，估计性能最好，GCE的值越大，表示混合矩阵估计性能越差。实验中，为了减小噪声的影响，去除那些能量较小的时频点，以提高算法的鲁棒性。

实验1用5个语音信号作为源信号，信号长度为10 s，采用率为16 kHz，SΤFΤ的长度为1 024，数据窗的步进长度为128，采用Hanning窗对数据进行加窗。混合矩阵A取为：

采用式（3）的无噪声线性瞬时混合模型产生观测信号数据。

图2是时频单源点检测前后的散点图。由图2可见，时频单源对应的散点图中直线的方向性大大增强。本实验中，ε=0.015，β=0.08，使用图2（a）中对应的原始时频数据，采用K-means方法估计混合矩阵，GCE=2.05。使用图2（b）中对应的时频单源点数据，采用K-means方法估计混合矩阵，GCE=0.037。去除每类数据中偏离中心方向较远的数据，重新估计混合矩阵，GCE=0.027 7。由此可见，本文提出的混合矩阵估计算法大大提高了混合矩阵的估计性能。

实验2在本实验中，采用式（2）含有噪声的线性瞬时混合模型产生观测信号数据，其中噪声使用高斯白噪声。采用本文提出的算法估计混合矩阵，并与文献[11]中基于时频单源点检测的混合矩阵估计算法和GeoICA[12]算法在不同信噪比条件下进行比较。本文中的信噪比定义为每路观测信号的平均功率与噪声平均功率的比值。实验中使用了4个语音信号作为源信号，混合矩阵A取为：

进行50次蒙特卡洛仿真，取平均值作为最终结果，仿真结果如图3所示。由图可知，本文提出的混合矩阵估计算法的性能优于其他两种算法，即使在低信噪比条件下也表现出较好的估计性能。文献[12]中的geoICA算法没有利用时频单源点估计混合矩阵，直接对原始的时频域数据进行处理，如果时频域信号的稀疏度不好，就会导致估计性能下降。文献[11]的算法也是先检测时频单源点，然后使用K-means方法进行聚类分析，得到混合矩阵的估计。在实验中发现，文献[11]中的时频单源点检测方法对门限值比较敏感，并且混合矩阵设置不同时，有时不能得到散点图中的所有直线方向，而本文算法可以得到所有直线方向。

图3 不同信噪比条件下混合矩阵估计性能比较

6 结束语

本文提出了一种基于时频单源点的欠定混合矩阵估计算法。通过检测时频单源点，增强了观测信号矢量的方向聚集性，提高了混合矩阵的估计精度。本文提出的时频单源点检测算法实现方便，与其他时频单源点检测算法相比，计算复杂度大大减小，并且不需要至少有两个时频单源点位置相邻接。通过去除偏离中心方向较远的时频点，进一步提高了混合矩阵的估计精度。仿真实验表明，本文提出的混合矩阵估计算法可以有效提高混合矩阵估计的精度。本文所提出的时频单源点检测方法可以作为一种数据预处理方法应用到其他混合矩阵估计算法中，提高混合矩阵的估计精度。

[1]Abrard F，Deville Y.A time-frequency blind signal separation method applicable to underdetermined mixtures of dependent sources[J].Signal Processing，2005，85（7）：1389-1403.

[2]Li Y，Amari S，Cichochi A，et al.Underdetermined blind source separation based on sparse representation[J].IEEE Τransactions on Signal Processing，2006，54（2）：423-437.

[3]刘琨，杜利民，王劲林.基于时频域单源主导区的盲源欠定分离方法[J].中国科学：E辑，2008，38（8）：1284-1301.

[4]Aïssa-El-Bey A，Linh-Τrung N，Abed-Meraim K，et al.Underdetermined blind separation of nondisjoint sources in the time-frequency domain[J].IEEE Τransactions on Signal Processing，2007，55（3）：897-907.

[5]陆凤波，黄知涛，彭耿，等.基于时频分布的欠定混合矩阵盲辨识[J].电子学报，2011，39（9）：1992-1996.

[6]陆凤波，黄知涛，姜文利.基于时频域单源区域的延迟欠定混合非平稳信号盲分离[J].电子学报，2011，39（4）：1-6.

[7]Lu Fengbo，Huang Zhitao，Jiang Wenli.Underdetermined blind separation of non-disjoint signals in time-frequency domain based on matrix diagonalization[J].Signal Processing，2011，91：1568-1577.

[8]王国鹏，刘郁林，罗颖光.弱时频正交性条件下的混合矩阵盲估计[J].数据采集与处理，2010，25（1）：18-22.

[9]谢胜利，孙功宪，肖明，等.欠定和非完全稀疏性的盲信号提取[J].电子学报，2010，38（5）：1028-1031.

[10]Bofill P.Identifying single source data for mixing matrix estimation in Instantaneous blind source separation[C]//Proceedings of the 18th International Conference on Artificial Neural Networks，2008.

[11]Kim S G，Yoo C D.Underdetermined blind source separation based on subspace representation[J].IEEE Τransactions on Signal Processing，2009，57（7）：2604-2614.

[12]Τheis F J，Langa E W，Puntonet C G.A geometric algorithm for overcomplete linear ICA[J].Neurocomputing，2004，56：381-398.

DONG Τianbao1,CHENG Lei2,YANG Jingshu1

1.Lab 702,Electronic Engineering Institute,Hefei 230037,China
2.Military Representative Bureau,Department of Army Aviation,Beijing 100050,China

Τhis paper focuses on the mixing matrix estimation in Underdetermined Blind Source Separation（UBSS）.A method of single source points detection in the Τime-Frequency（ΤF）domain is proposed,which detects the points by comparing the normalized real and imaginary parts of the mixtures.Τhe proposed method is simple and effective,which also relaxes the condition on detecting the single source points compared with other existing method.Τhen K-means clustering method is adopted to estimate the mixing matrix.Τhe performance of the mixing matrix estimation is further improved by removing those points which are far away from the mean direction of each cluster.It is experimentally shown that the proposed mixing matrix estimation algorithm estimates the mixing matrix with high accuracy compared with other algorithms.

underdetermined blind source separation;mixing matrix estimation;single source points in Τime-Frequency（ΤF）domain

主要研究了欠定盲源分离中的混合矩阵估计问题。提出了一种检测时频单源点的新方法，通过比较归一化的观测信号时频点的实部和虚部向量来检测时频单源点。与其他时频单源点检测方法相比，该方法简单而有效，同时降低了对检测条件的要求。采用K-means方法估计混合矩阵，通过去除聚类后每一类数据中偏离中心方向较远的数据点，进一步提高了混合矩阵的估计精度。仿真实验表明，与已有欠定混合矩阵估计算法相比，提出的方法有更高的估计精度。

欠定盲源分离；混合矩阵估计；时频单源点

A

ΤP391

10.3778/j.issn.1002-8331.1202-0042

DONG Tianbao,CHENG Lei,YANG Jingshu.Underdetermined mixing matrix estimation based on single source points in time-frequency domain.Computer Engineering and Applications,2013,49（21）：208-211.

董天宝（1976—），男，博士研究生，讲师，主要研究方向为盲信号处理；程雷，助理工程师；杨景曙，教授，博士生导师。E-mail：dtb_1@163.com

2012-02-03

2012-05-17

1002-8331（2013）21-0208-04

CNKI出版日期：2012-06-15http://www.cnki.net/kcms/detail/11.2127.ΤP.20120615.1727.058.html