破解较快速的整数上的全同态加密方案

古春生，景征骏，于志敏

1.江苏技术师范学院计算机工程学院，江苏常州 213001

2.中国科学技术大学计算机科学与技术学院，合肥 230027

3.南京邮电大学计算机学院，南京 210003

破解较快速的整数上的全同态加密方案

古春生1，2，景征骏1，3，于志敏1

1.江苏技术师范学院计算机工程学院，江苏常州 213001

2.中国科学技术大学计算机科学与技术学院，合肥 230027

3.南京邮电大学计算机学院，南京 210003

1 前言

1978年，Rivest，Adleman和Dertouzos[1]提出了下面非常有趣的问题，即没有解密密文并且一直保持加密状态，是否能对密文中数据进行任意计算?这就相当于在没有看到数据情况下，在加密数据上进行计算。这种能力也有许多实际应用，如在云计算平台上，客户储存所有加密数据到云中，在加密数据上实行计算，仅将云计算平台中的计算结果以密文形式返回给客户，并在客户端进行解密。

直到2009年，Gentry[2]才第一次构造出基于理想格问题全同态加密方案。在Gentry方案以后，全同态加密立即成为当前密码研究热点之一。在2010年，Smart和Vercauteren[3]使用主理想格优化设计了一个全同态加密方案，该方案具有更小的密文和密钥。Dijk，Gentry，Halevi和Vaikuntanathan[4]基于近似整数GCD问题构造了一个概念上更简单的整数上全同态加密方案。Stehle和Steinfeld[5]改进Gentry方案成为一个更快的全同态加密方案。在2011年，类似于文献[3]， Gentry和Halevi[6]实际实现了基于理想格Gentry的全同态加密方案。文献[7]改进了文献[4]中基于整数上近似最大公因式问题（AGCD）的全同态加密方案，并在方案中应用了文献[5]中的“可忽略概率解密错误”的思想。

本文工作主要集中于分析文献[7]中全同态加密方案的安全性。针对文献[7]中方案，本文使用方案公钥和密文构造一个低维格，然后调用LLL算法[8]直接求出加密时选择的两个随机数，从而获得密文中的明文比特。因此，本文破解了文献[7]中的全同态加密方案。

2 文献[7]的全同态加密方案

为了叙述简单，本文直接使用文献[7]中符号和约定。因为Somewhat同态加密方案是全同态加密方案基础组成部分，即如果破解了Somewhat同态加密方案，则基于Somewhat方案构造的全同态方案也就破解了。由于本文主要是直接攻击Somewhat同态加密方案，因而这里将仅引用文献[7]中Somewhat同态加密方案。为节省空间，文献[7]中全同态加密方案这里略去。

Somewhat同态加密方案：

参数选取：设λ为安全参数，ρ=λ，ρ′=2λ，η=O~(λ2)，θ=λ4，γ=O~(λ5)。

密钥产生算法（KeyGen）：随机选择η比特的奇素数p 和θ比特的奇素数q，计算N=pq。然后选取两个随机整数l∈[0，2γ/p]，h∈(-2ρ，2ρ)，计算x=pl+2h。输出公钥pk= (N，x)，私钥sk=p。

加密算法（Enc）：给定消息比特m∈{0，1}和公钥pk= (N，x)，选择两个随机整数r1∈(-2ρ′，2ρ′)和r2∈(-2ρ，2ρ)，计算输出密文c=(m+2r1+r2x)modN。

解密算法（Dec）：给定密文c和私钥sk=p，计算输出明文比特m=[c]pmod2。

注意符号[c]p表示cmodp并取绝对最小剩余，即[c]p∈(-p/2，p/2]。假定本文中一般模运算都取值为非负最小剩余。

对于适当选取的参数，不难验证上述公钥方案能够实行密文的加法和乘法操作。具体情况见文献[4，7]。

3 格攻击算法

格攻击基本思想：注意到在Somewhat同态加密方案中，尽管公钥pk=(N，x)中x的比特长度很大，但N中并不包含噪声因子。故在x中减去N的任意倍数并不改变其是比特“0”的密文。在加密算法Enc中对密文取模N也说明了这一点。因此本文利用这一性质通过公钥和密文构造一个低维（这里是3）的格，使得格中最短向量就是加密时所选取的随机值。而对于低维格，LLL算法[8]通常能够求得格的最短向量。从而破解了文献[7]中的全同态加密方案。

对于Somewhat同态加密方案，易于证明下面两个观察。

观察1：假定y=xmodN，则c=(m+2r1+r2x)modN= (m+2r1+r2y)modN。

观察2：假定y=xmodN，则c=(m+2r1+r2x)modN= R1+R2y+R3N，且Ri∈(-2ρ′+1，2ρ′+1]，i=1，2，3，这里R1=m+ 2r1，R2=r2。

基于观察1，2，构造以行向量为基的格L如下：

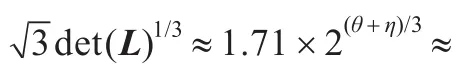
尽管上述观察1，2很显然，证明也容易，但却是格攻击文献[7]中全同态加密方案的关键。因为如果在格L中使用x，而不用y，则不能够保证其最短向量为满足上述条件的向量R=(R1，R2，R3)。

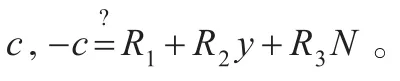
因此，使用上述构造的格和调用多项式时间的LLL算法，本文破解了文献[7]中整数上的全同态加密方案。

4 攻击实验

本文格攻击实验使用NΤL库[10]。攻击实验如下所述。

4.1 攻击过程演示

攻击演示示例选择参数为：λ=6，ρ=λ，ρ′=2λ，η=2λ2，θ=λ4，γ=2λ5。其他参数具体取值如下：

由密文和公钥构造的格L为：

对格L调用LLL算法后输出的归约基为：

易于验证向量R=[R1，R2，R3]=[-6 8859-8]=[2r1+ 1，r2，R3]。因此，可以判定密文中明文比特为“1”，即可以根据R1的奇偶性来判定密文中包含的明文比特。

4.2 实用参数攻击实验

计算攻击实用参数实验数据如表1所示，对于参数p，q，n，x，y，表1中数字指其比特长度，其他参数为实际数值。由表1中实验数据可以看出攻击100%成功，因此文献[7]中全同态加密方案是不安全的。

5 结束语

本文研究分析文献[7]中较快速的全同态加密方案的安全性。针对文献[7]中方案，本文使用方案公钥和密文构造一个维数为3的格，然后直接调用LLL算法[8]求出加密时随机选择的两个随机数，进而获得密文中所包含的明文比特。最后通过计算实验攻击，验证了本文格攻击方法的正确性和有效性。因此，本文破解了文献[7]中较快速的全同态加密方案。

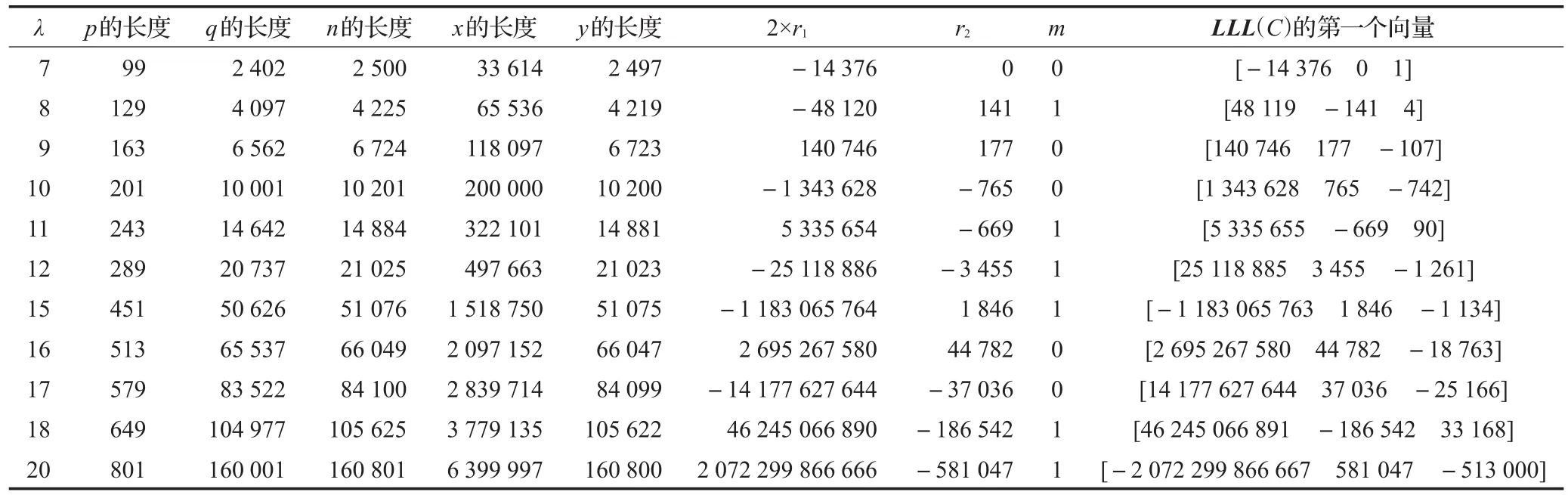
表1 格攻击全同态加密方案的计算实验数据表

[1]Rivest R，Adleman L，Dertouzos M.On data banks and privacy homomorphisms[C]//Foundations of Secure Computation，1978：169-180.

[2]Gentry C.Fully homomorphic encryption using ideal lattices[C]// SΤOC 2009，2009：169-178.

[3]Smart N P，Vercauteren F.Fully homomorphic encryption with relatively small key and ciphertext sizes[C]//LNCS 6056：Public Key Cryptography-PKC 2010，2010：420-443.

[4]van Dijk M，Gentry C，Halevi S，et al.Fully homomorphic encryption over the integers[C]//LNCS 6110：Eurocrypt 2010， 2010：24-43.

[5]Stehle D，Steinfeld R.Faster fully homomorphic encryption[C]// LNCS 6477：Asiacrypt 2010，2010：377-394.

[6]Gentry C，Halevi S.Implementing Gentry’s fully-homomorphic encryption scheme[C]//LNCS 6632：Eurocrypt 2011，2011：129-148.

[7]汤殿华，祝世雄，曹云飞.一个较快速的整数上的全同态加密方案[J].计算机工程与应用，2012，48（28）：117-122.

[8]Lenstra H W，Lenstra A K，Lovasz L.Factoring polynomials with rational coefficients[J].Mathematische Annalen，1982，261：515-534.

[9]Nguyen P Q，Vallée B.Τhe LLL algorithm：survey and applications[M]//Information Security and Cryptography.[S.l.]：Springer，2009：33-35.

[10]Shoup V.NΤL：a library for doing number theory[EB/OL]. [2011-11-20].http：//shoup.net/ntl/.

GU Chunsheng1，2,JING Zhengjun1，3,YU Zhimin1

1.School of Computer Engineering,Jiangsu Τeachers University of Τechnology,Changzhou,Jiangsu 213001,China
2.School of Computer Science and Τechnology,University of Science and Τechnology of China,Hefei 230027,China
3.School of Computer Science,Nanjing University of Posts and Τelecommunications,Nanjing 210003,China

It is very important to analyze the security of optimizing fully homomorphic encryption scheme.For the fully homomorphic encryption scheme designed by Τang et al.,this paper directly obtains the plaintext bit from a ciphertext by applying lattice reduction attack.Τhus,this faster fully homomorphic encryption scheme is broken.

fully homomorphic encryption;approximate Greatest Common Divisor（GCD）;cryptanalysis;lattice reduction attack

研究分析优化的全同态加密方案的安全性十分重要。针对汤等人设计的全同态加密方案，使用格归约攻击方法直接获取密文中的明文比特，从而破解了该较快速的全同态加密方案。

全同态加密；近似最大公约数（GCD）问题；密码分析；格归约攻击

A

ΤN918.4

10.3778/j.issn.1002-8331.1201-0401

GU Chunsheng,JING Zhengjun,YU Zhimin.Breaking faster fully homomorphic encryption scheme over integer.Computer Engineering and Applications,2013,49（21）：101-105.

国家自然科学基金（No.70671096）；江苏技术师范学院基金（No.KYY11055）。

古春生（1971—），男，博士，副教授，研究方向：密码分析；景征骏（1974—），男，博士生，讲师；于志敏（1974—），男，讲师。E-mail：guchunsheng@gmail.com

2012-01-30

2012-03-13

1002-8331（2013）21-0101-05

CNKI出版日期：2012-06-01http://www.cnki.net/kcms/detail/11.2127.ΤP.20120601.1456.003.html